Ranking Grid-sites based on their Reliability for Successfully Executing Jobs of Given Durations

Published Online April 2015 in MECS DOI: 10.5815/ijcnis.2015.05.02

• I.    Introduction

  With the maturity of distributed technologies the composition, scale and utilization of distributed systems is continuously evolving. The large scale distributed systems like Grids and testbeds under centralized administrative controls, such as, EGEE[13], Planet Lab[5], Open Science Grid[34], Tera Grid [33], Grid’5000 [2] etc. consist of hundreds/thousands of resources [30]. These systems/environments may even include resources available for short periods, such as computers from university labs, Public Resource Computing (PRC) systems [4] and on demand resources [30]. To select the most suitable resources from such a large pool where resources vary considerably in terms of their properties, Grid high level services need to know how reliable a Grid-site is for successful execution of a job of given duration. For example, Grid resource

manager requires Grid-sites reliability to filter out and allocate suitable resources for given requests. Grid schedulers need Grid-sites reliability to map given set of activities to available resources. Performance monitoring services require Grid-sites reliability for their performance analysis.

The reliability of a Grid-site for successful execution of a job mainly depends upon availability of the Grid-site and its capacity of fault free execution of a job. The availability of a Grid-site depends upon several factors including nature of the environment the Grid-site originally belongs to, the resource owners’ policies for sharing their resources in the Grid, etc. [30]. In addition, the resources may also be disconnected from the Grid environment for regular maintenance, unexpected faults, or other projects. Due to diversification of the Grid environment, complexities of the technologies involved, and the support provided by the resource owners, the jobs submitted to the Grid-sites may not execute successfully and fail. Moreover, the jobs may also fail due to several other faults [20] in the Grid environment, which may occur at any stage during job execution due to Grid middleware, software stack on the Grid-site, unavailability of required libraries, execution time restrictions from local resource manager, etc. All these factors make reliability modeling of a Grid-site for successful execution of a job a challenging problem.

To address this problem, in this paper, we model reliability of a Grid-site for successful execution of a job. To be precise we define reliability of a Grid-site as its degree to which it can accept and execute jobs successfully. Our model considers future availability of the Grid-site for the given duration of job execution as well as possibility of fault free execution of the job. The future availability of the Grid-site is predicted using a state of the art method based on Bayesian Inference. The possibility of fault free execution of a job is measured as probability of successful execution based on past submitted jobs. This is later referred as job success rate. Both of these measurements require trace data of Grid-site availability and job executions. For our present study, we considered real traces of a national Grid (the name hidden due to privacy reasons). The results of our experiments are presented in this paper. Our experiments show that considering only Grid-site availability or job success rate leads to suboptimal ranking of Grid-sites. However, considering Grid-site reliability through our proposed model yields optimized ranking of Grid-sites.

We use the following terminology in this paper. By Grid-site we refer to a Grid resource that can accept and execute a computation request referred as a job request (or simply a job). A Grid-site is considered available if it is turned on and can accept job requests; otherwise, it is considered unavailable. Please note that we use the terms Grid-site and Grid resource interchangeably.

The rest of the paper is arranged as follows. The section II describes major characteristics of Grid-sites that are important to understand the overall reliability modeling proposed in this paper. Section III precisely describes our problem statement. Section IV describes our method of reliability modeling. The subsections IVA and IVB describe our methods for predicting Grid-site availability and assessing job success rate. Section V describes our experiments and associated findings. The related work is presented in section

• VI. Finally, we conclude and describe the future work in section VII.

• II.    Characteristics Of Grid-Sites And Large Scale Scientific Applications

Grid-sites in medium and large scale Grids are usually contributed by different organizations, yet their ownerships remain with the parent organizations. These organizations have their own policies for sharing their resources in the Grid. In general, the Grid-sites are typically characterized by their dynamic availability. Besides the resources dedicated to Grid environment, other resources are contributed for some specific durations of time (like during working hours of working days etc.). The parent organizations may remove their resources from the Grid environment for their own special needs like projects etc. Some resources are contributed in the Grid depending upon their usage by local users – the resources are available in the Grid if not in use by a local user; as soon as the local user starts working on the resource, it is taken out of the Grid. The examples of such resources include desktop computers from computer labs and P2P environments. The resources may also be taken out of the Grid for regular maintenance, updates, etc. The resources may also be unavailable due to some faults. In nutshell, Grid-sites vary largely in their availability properties that must be taken care of while selecting a Grid-site for a job execution.

Besides their computational resources and storage capacity, Grid-sites also vary with respect to available software stacks, their maintenance, software updates etc. Due to these variations and several other possible faults [20], the jobs submitted to Grid-sites may fail. Therefore, it is important to evaluate Grid-sites for their job success rate in the past.

Scientific applications are an important class of applications that require large scale computing and/or data management infrastructures like Grid [32, 29, 27, 28]. These applications usually consists of several activities/tasks with complex execution and data dependencies [22,  37,  35], referred as large scale applications. To exploit possible parallelism of these applications, some activities are executed in parallel on multiple Grid-sites. The overall execution time of large scale scientific applications ranges from minutes to hours and even days. The efficient execution of these applications requires uninterrupted availability of several Grid-sites for a long time. However, due to dynamic availability of Grid-sites, selection of the Grid-sites that will remain available for the duration of application execution is very challenging and requires prediction of their availability.

• III.    Problem Statement

The Grid users and high level Grid middleware services, like met schedulers and resource managers, need to rank the available Grid-sites for their reliability of executing a given job successfully and then select/allocate the best Grid-site for executing the job. The reliability of a Grid-site for executing a given job successfully depends upon its availability properties as well as its rate of executing jobs successfully. The availability properties of a Grid-site can be determined from its past records of being available for different time durations. More specifically, Grid-site’s availability for the duration of job execution as well as for the higher duration is of particular interest.

Ranking of the available Grid-sites requires reliability modeling of the Grid-sites. To model reliability of the Grid-sites for successful execution of given jobs, we describe the problem statement as follows.

What is the reliability ( R ) of a Grid-site g ( Rg ) that has been available for different time durations [ d 1 ,d 2 ,d 3 ,...,d n ] throughout its life time and have a job success rate of λg for successfully executing a job of execution time t ?

We describe our proposed approach to model Grid-site reliability in the following section.

• IV.    Modeling Reliability Of Grid-Sites

We model reliability of a Grid-site in terms of Grid-site availability and job success rate. The future availability of the Grid-site is predicted using Bayesian Inference [31] and the job success rate is calculated from Grid-site’s trace of job executions. These methods are described in detail in the following sections.

• A.    Grid-site Availability Predictions

We predict Grid-site availability using Bayesian Inference. Bayesian Inference estimates possibility of an event from its likelihood and prior probability (priori) conditional to its properties. Thus, Bayesian Inference by nature exploits resource availability properties by incorporating its patterns of availability from past traces as well as current behavior. In this work, we consider only two states of a Grid-site, “available” and “unavailable”. We define Bayesian Inference for our two class resource state as follows. Let θ1 and θ2 represent the two classes to which our Grid-site state belongs. The priori probabilities of the two states, P (θ1) and P (θ2), can be calculated as follows. If N is the total number of events and n1, n2 belong to θ1 and θ2, respectively, then

P ( θ 1 ) =                        (1)

and

P ( θ 2 ) =                        (2)

Let p ( d j |θ_i ) (for i = 1, 2, j = 1, 2, ..., n ) represents the class conditional probability density functions (PDFs), describing the distribution of feature d j in each class. Here, the feature set D consists different time durations for which the Grid-site has been available.

D = [ d 1 , d 2 , d 3 , ..., d n ]

These time durations are extracted in Grid-site availability characterization phase [31]. The class conditional PDFs are also calculated from the trace data during the characterization phase. Then, according to Bayesian Inference:

P (θi |dj) = ? ( | ( ) )(а)

()

where p ( d j ) is the PDF of d j and in our case it can be calculated as:

р( d})=∑Lp( dj | et)p(et )

We consider one feature from the feature set D at a time, which can have any value from its feature space. In our case, feature set only takes discrete values and thus the density functions p ( d j | θ i ) become probabilities, which are calculated as P ( d j | θ i ).

Bayesian Inference shows that we can convert the priori P (θi) to a posteriori (or posterior probability) P (θi | dj) – the probability of the state of nature being θi given that feature value dj has been used. We call p(dj | θi) the likelihood of θi, a term chosen to indicate that other things being equal the class θi for which p(dj | θi) is large is more likely be the true class. Bayes’ formula can be expressed informally by saying that likelihood ×priori posteriori =                           (5)

Thus in our work, the availability α of a Grid-site for the time duration d j is modeled as its posterior probability of the Grid-site for being in state “available” for the time d j :

α ( d j ) = P ( available | d j )              (6)

• B.    Job Success Rate

The job success rate λ of a Grid-site g is defined as ratio of number of jobs completed successfully ( N_c ) on that Grid-site to the number of jobs submitted ( N s ) to it.

λ = g N<

• C.    Reliability Model

We model reliability R of a Grid-site g available for different time durations [ d₁, d₂, d₃,..., d_n ] during its whole life time and having a job successful rate λ , for successfully executing a job with execution time t as:

Pg

( t ) =∑ a ( dj )× ^g ∀

For a Grid-site g :

∑ a (dj)=1

Thus,

∑∀ dj>t  ( dj)< 1

Also,

^9≤1

Therefore,

0≤ Pg (t)<1

It means that the reliability of a Grid-site ranges between 0 and 0.99.

• V. Experiments

To demonstrate the effectiveness of the proposed approach, we modeled reliability of several Grid-sites in a national Grid (the names of the Grid and Grid-sites are anonymized due to privacy reasons). The availability of Grid-sites was monitored for a period of one year and their states (available or unavailable) were stored after every five minutes. This availability trace was used in Bayesian Inference to predict the availability. A random time ( t ) from the availability trace was selected and the trace data before t was used in Bayesian Inference to predict the availability of the Grid-site at time t . The probabilistic availability predicted through Bayesian Inference was then used in our availability model. The log data gathered by local job submission systems on the Grid-sites was used to calculate the job success rate at time t .

First we present the reliability (modeled through the proposed approach) of four representative Grid-sites (two from the computer labs and two Grid-sites dedicated to the Grid for production purposes). Figures 1 and 2 show the reliability of two Grid-sites from university computer labs for executing jobs of different durations (from less than one hour to 11 hours). The job success rate on these two Grid-sites was 85% and 93%, respectively. As these sites were available for small durations, their reliability decreased sharply as the duration of job execution increased.

Figures 3 and 4 show the reliability of two dedicated Grid-sites for executing jobs of different durations (from less than one day to 11 days). These Grid-sites were meant to be available all the times for production purposes. Although the dedicated Grid-sites remained available for more than 11 days, for simplicity reasons we have shown data for 11 days only. The job success rates on these two sites were 98% and 99%, respectively. Since these Grid-sites were mostly available for longer time durations, their reliability decreased at a smaller rate than that of Grid-sites from the Computer labs.

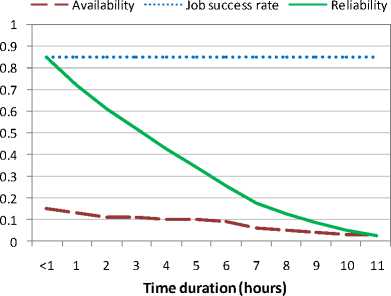
Fig. 1. Reliability of a Grid-site 1 (from computer labs) for executing jobs of different durations

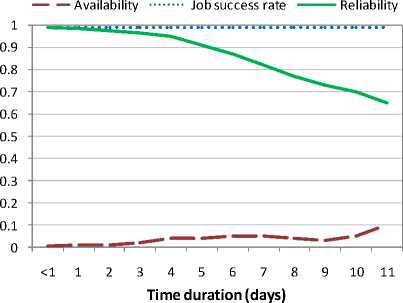
Fig. 4. Reliability of a Grid-site 4 (production site dedicated for Grid users) for executing jobs of different durations.

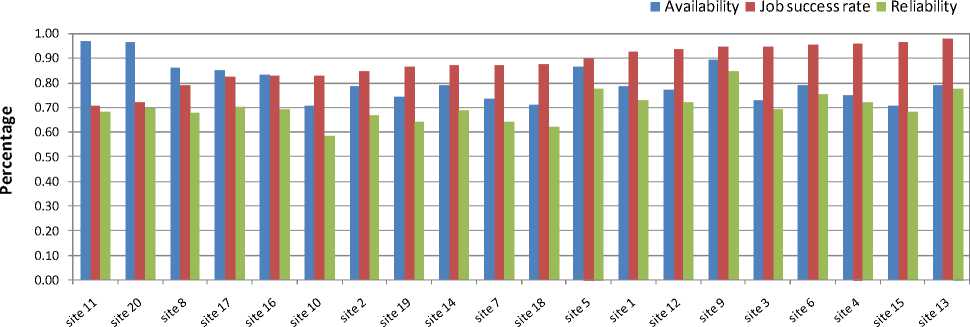
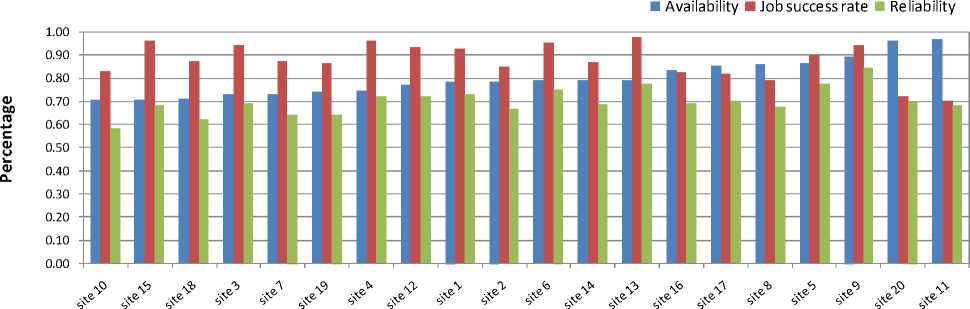
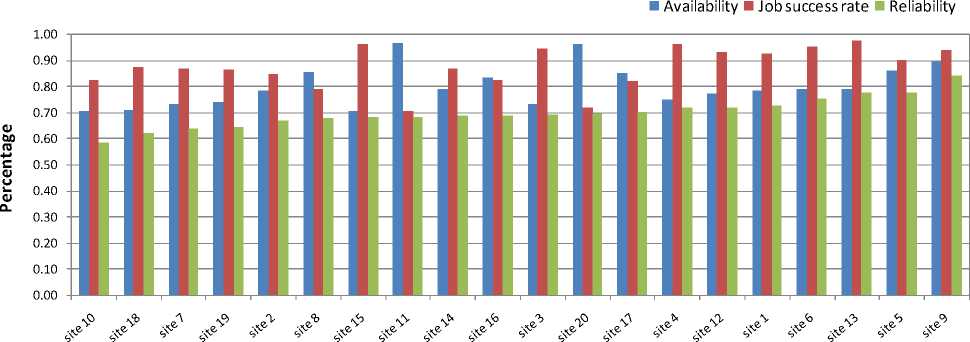
Next, we compared 20 Grid-sites at particular time for their job success rate, availability and reliability for a job of 30 minutes duration. Their respective rankings are shown in figures 5, 6 and 7. It can be observed that the Grid-sites ranked differently when the criteria (job success rate or availability or reliability) for ranking the Grid-sites varied. It can also be observed that considering one factor at a time (i.e. job success rate or availability) will result in a different ranking and thus will be suboptimal. However, ranking based on reliability (that considers both availability and job success rate) results in optimal order.

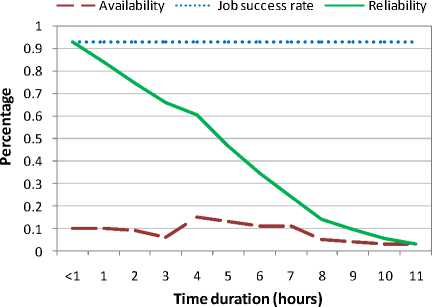
Fig. 2. Reliability of a Grid-site 2 (from computer labs) for executing jobs of different durations.

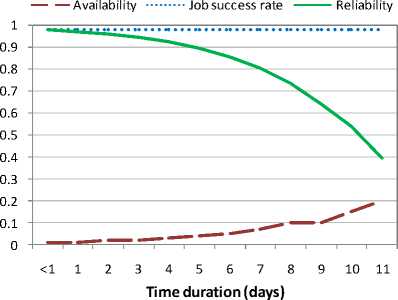
Fig. 3. Reliability of a Grid-site 3 (production site dedicated for Grid users) for executing jobs of different durations.

VI. Related Work

There have been several efforts for quantifying the reliability of resources in distributed systems, like in [36, 25, 17, 3]. These efforts are mainly based on architectural considerations of distributed systems. However, it is very difficult to compute reliability of arbitrary structured distributed systems [24]. Xie et al. [38] modeled reliability of hardware systems, software, integrated systems, distributed computing systems and Grid computing systems.

Xie et al. [38] also modeled overall reliability of Grid computing systems based on known failure rates of nodes, links and other known components. Later Dai et al. [6] refined the work by Xie et al. [38] by considering a hierarchical model of the Grid. The authors used Markov chain to model probabilities of different failures. In their work Dai et al. [6] modeled reliability of collection of Grid resources communicating on shared links. Later in [8, 7, 9], the authors modeled reliability and performance of services in a tree structured Grid using graph theory and probability theory. The authors also extended their work for optimal allocation of Grid resources to maximize the reliability of services in a tree structured Grid. Graph theory based methods have also been employed for reliability assessment by Dakil et al. [10]. Levitin et al. [26] modeled reliability and performance of services in Grid computing systems with star architectures. However, these work mainly considered job failure rate of Grid resources/services.

Grid-sites

Fig. 5. Ranking of 20 Grid-sites for their job success rate in the Grid. (The right-most Grid-site has the highest rank).

Grid-sites

Fig. 6. Ranking of 20 Grid-sites for their availability in the Grid. (The right-most Grid-site has the highest rank).

Grid-sites

Fig. 7. Ranking of 20 Grid-sites for their reliability in the Grid. (The right-most Grid-site has the highest rank).

Gholami et al. [15] proposed a Monte Carlo simulation based algorithm to estimate reliability of Grid programs and the whole Grid system. To estimate the reliability of involved nodes and links, their algorithm considers rate of data transmission through the links and the processing time on nodes. Later, these authors improved their work to maximize the reliability of Grid computing systems using Simulated Annealing [16]. The authors in [14]

proposed a Graph theory and Bayesian networks based algorithm to estimate reliability and latency of Grid computing systems. Like others [1], the authors also consider rate of data transfer through the links among Grid nodes. Beside others, Kuar [23] and Gran et al. [18] also used Bayesian networks to estimate reliability. Doguc et al. [12] proposed a holistic method for estimating system reliability using Bayesian networks. The authors employed K2 data mining algorithm to find associations between the system components. In their later work [11], the authors further improved their work by making their approach independent of any prior knowledge about the grid system structure. The authors used K2 algorithm to automatically discover the structure of Grid system from historical data and to find minimum resource spanning trees (MRST) in the Grid. In next step, the authors used Bayesian networks to model the MRST and estimate reliability of the Grid. Guo et al. [19] modeled reliability of Grid services based on Local Node Fault Recovery (LNFR) mechanism and demonstrated the influence of fault recovery on Grid service reliability. Hussin et al. [21] modeled reliability in resource management for distributed systems through adaptive reinforcement learning. The methodology of reinforcement learning is used in conjunction with neural network to help Grid scheduler adapt to dynamic changes in Grid environment.

In contrast, our focus is on modeling reliability of Grid-sites for successful execution of Grid jobs. To model Grid-site reliability, we consider Grid-sites’ availability for the duration of job execution as well as previous job success rate on the Grid-site. To the best of our knowledge, we are the first to rank the Grid-sites based on their future availability for the duration of job execution as well as their job success rate. This reliability measure is helpful for Grid users, meta schedulers and resource managers in optimized ranking of Grid-sites for their possibility of executing a job successfully. We have also demonstrated through our experiments that considering either job success rate or availability results in sub-optimal selection of Grid-sites.

• VII. Conclusion And Future Work

Grid schedulers, resource manager and performance analysis services require Grid-site s’ ranking based on their reliability for successful execution of Grid jobs. Modeling reliability of a Grid-site for successful execution of a job requires predictions about its availability for the duration of job execution as well as its job success rate. Effective predictions of Grid-site availability requires past patterns of resource availability. We predict Grid-site availability using methods from pattern classification and recognition, which incorporate resource past behavior. The job success rate is calculated as probability of successful job executions using trace data. Our method can effectively rank Grid-sites to optimize reliability of Grid-sites for successful execution of jobs. In future, we plan to evaluate our reliability model using other methods of resource availability predictions. We also plan to develop methods to cross verify our reliability measurements.