Расчет безопасного ресурса зданий и сооружений

Время безопасной эксплуатации (ресурс) здания зависит от степени деградации его несущих конструкций, происходящей под влиянием различных системоразрушающих факторов (дефекты, старение, коррозия и др.). Интегральными показателями деградации являются физический (конструкционный) износ объекта и величина его фактического риска аварии.

В работе [1] за риск аварии объекта принята величина г, равная отношению фактической вероятности аварии здания к теоретической вероятности, закладываемой по умолчанию в объект при его проектировании. Величина г является случайной и на неограниченном множестве /и-этажных зданий плотность ее вероятности подчиняется закону Рэлея [1]:

№ = (г-1)/а² ■ ехр[- (г - 1)²/2 ст²], (1) где параметр сг связан с математическим ожиданием (средним значением) риска аварии R соотношением:

R = 1 + 1,25<т, (2)

Закон распределения (1) позволяет извлечь информацию о степени неопределенности технического состояния объекта. Такую информацию предоставляет энтропия риска аварии Н, определяемая по формуле [2]:

tf=-W/)log₂TW (3) где РСА,) - вероятность события, заключающегося в том, что риск аварии находится в z-м диапазоне значений риска, определяемых уравнением (1).

На рис. 1 приведен построенный на основе машинного эксперимента с формулами (1), (2) и (3) график функции H(R) (пунктирная линия), показывающий зависимость энтропии от величины математического ожидания R закона (1) распределения риска аварии. Этот график аппроксимирован уравнением (сплошная линия) вида

Известно [3], что любое изменение скорости энтропии информирует об изменении технического состояния объекта. На рис. 2 показана модель деградации несущего каркаса объекта, полученная выделением на кривой, показанной на рис. 1, три линейных участка, на стыке которых скорость энтропии скачкообразно меняется. Решение о расположении стыковых точек на этой модели принято на основе анализа результатов оценки риска аварии, полученных при диагностике технического состояния зданий различного срока эксплуатации (новых, подержанных, аварийных и ветхо-аварийных).

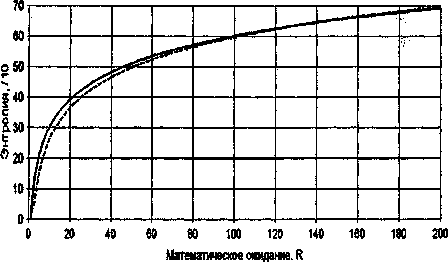
Рис. 1. Зависимость энтропии от среднего значения риска аварии

Н (энтропия)

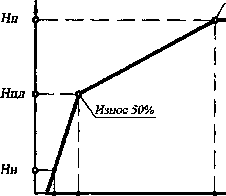
Кв = 2- нормальный (естественный) риск аварии

Кпд =21 - предельно-допустимый риск аварии

Rn = 93- предельный риск аварии

R (риск аварии)

Износ 95%

1 Rh Кпд              Кп

Рис. 2. Модель деградации несущего каркаса объекта

Полученная модель (рис. 2) позволяет утверждать:

• 1.    Если риск аварии объекта не превы'шает предельно-допустимого значения, равного R^ = 21, то состояние объекта следует трактовать как безопасное. В этом состоянии несущий каркас объекта способен сопротивляться не только проектным нагрузкам, но и неучтенным при проектировании нагрузкам в виде перегрузок, возникающих в чрезвычайных ситуациях (непроектные воздействия).

• 2.    Превышение риском аварии предельнодопустимого значения означает переход объекта в аварийное состояние, при котором вероятность появления в несущих конструкциях трещин (предвестников аварии) становится ощутимой. В этом состоянии сопротивляемость несущего каркаса объекта непроектным воздействиям снижается, а с дальнейшим ростом риска аварии полностью исчерпывается. Как будет показано ниже, при достижении объектом предельно-допустимого риска величина его физического (конструкционного) износа составляет ~50 %. При такой величине износа требуется капитальный ремонт здания [4] с целью восстановления способности его несущего каркаса сопротивляться непроектным воздействиям. Если ремонтно-восстановительные мероприятия на объекте произведены не будут, то риск аварии растет и время достижения предельного значения риска, равного R_n = 93, определяет предельный ресурс Т_п объекта.

Экспертиза и оценка объектов недвижимости

Безопасным ресурсом 76 объекта является время его эксплуатации объекта с момента окончания строительства до достижения предельно-допустимого значения риска аварии.

З.При достижении риском аварии предельного значения максимальной становится не только энтропия риска, но и величина конструкционного износа объекта. При R > R_n способность несущего каркаса объекта сопротивляться любым нагрузкам теоретически исчерпывается. Такое состояние объекта принято считать ветхо-аварийным [4].

Безопасный ресурс здания, его физический (конструкционный) износа и фактический риск аварии - тесно связанные величины. При построении математических моделей для определения физического износа и ресурса объекта приняты две гипотезы:

• 1.    Формой модели роста физического износа объекта в процессе его эксплуатации является экспонента. Ее представительным параметром служит фактический риск аварии R^, зафиксированный через 7ф лет эксплуатации объекта.

• 2.    К моменту времени эксплуатации, когда риск аварии объекта достигает предельного значения R_m физический износ объекта становится равным 0,95 (95 %).

Выбор формы модели физического износа объекта (1-я гипотеза) обоснован исследованиями ресурса конструкций в теории надежности [5], а вторая гипотеза введена по аналогии с «гамма» % ресурсом по износу, используемым в теории надежности [5].

Принятым гипотезам отвечает математическая модель, имеющая вид:

У_ф = ЛГ) = 1 - ехр{-0,0325(Л_ф - 1)}. (5)

Математическая модель (6) позволяет оценить физический износ (Уф) эксплуатируемого здания (сооружения) на момент времени Т. При Rф = 1 (момент начала строительства) формула (5) дает нулевой износ объекта, а при подстановке в фор- мулу (5) Rф = Rn = 93 физический износ объекта равен 0,95. Износ при достижении объектом предельно-допустимого риска аварии 7?ф = Rm =21 равен Увд= 0,48 (48 %).

В математической модели (5) фактор времени присутствует в неявном виде. Им является зафиксированный момент времени Т =Т_С + 7ф, где 7_С -время возведения (строительства) объекта, а 7_Ф -срок эксплуатации объекта, при котором произведена диагностика его технического состояния и рассчитан риск аварии, позволяющий по формуле (5) определить фактический износ объекта У_ф на момент времени Т. Для расчета безопасного остаточного ресурса здания зависимость физического износа от времени в явном виде по аналогии с выражением (5) также принимается в форме экспоненты:

У(7) = 1-ехр{-/• 7}, (6) где z - интенсивность физического износа объекта, определяемая из условия, что при Т = Т_с + Тф, величина износа известна и равна Уф = У(7).

Безопасный остаточный ресурс 7^ определится по формуле

7_6о=7_пд-7, (7) где 7_та - время от начала строительства объекта до достижения им предельно-допустимого значения риска аварии Время 7_ВД при найденном значении интенсивности найдется из уравнения (6), если принять, что У(7 = 7щ) = Уцд = 0,48. Величина Т_па также можно определить из формулы, вытекающей из равенства правых частей зависимостей (5) и (6): {-0,0325(7?пд - 1)} = {-/ ■ T_ra). Из этой формулы следует, что

7ад=0,65//. (8)

Очевидно, если 7?ф >  R^ безопасный остаточный ресурс объекта равен нулю.

Предельный срок службы объекта (7П) можно спрогнозировать из условия, что при 7 = 7О + 7С износ, согласно приятой гипотезы, известен и равен У(7П + 7С) = Уп = 0,95. Здесь время (7„ + 7С) также можно определить из равенства: {-0,0325(Лп - 1)} = = {-z • (7П + 7С)}, из которого следует, что

7П=2,99//-7С. (9)

Безопасный ресурс объекта существенным образом зависит от величины фактического риска аварии на момент сдачи его в эксплуатацию. Действительно, пусть после окончания строительства фактический риск аварии объекта нормальный (Дф = R_H = 2), а срок строительства был 7_С = 2. Из формулы (5) следует, что фактический износ объекта к моменту сдачи его в эксплуатацию составил Уф = 0,0319 (3,19%). Из формулы (6) определим интенсивность износа / = 0,01625 (1/лет), а при найденной величине интенсивности по формуле (8) находим время (7вд) до достижения объектом предельно-допустимого риска R^ Т_ш = 40 лет. Из формулы (7) следует, что безопасный ресурс объекта составил 7б= 38 лет.

Теперь предположим, что фактический риск аварии объекта после окончания его строительства

Мельчакое А.П., Косогоров В.Г., Никольский И.С.

превысил нормальное значение в два раза, т.е. Кф = 2Л_Н = 4. В этом случае Аф = 0,0929 (9,29 %); / = 0,04875 (1/лет); Т^ 0,65/0,04875 = 13,3 лет; Т_б⁼ 13,3 - 2 = 11,3 лет. Следовательно, превышение нормального значения риска аварии к окончанию строительства объекта в 2 раза, снизило безопасный ресурс объекта в 3,36 раза. Такова плата за превышение нормального значения риска аварии при строительстве зданий и сооружений.

В заключение следует отметить, что для эксплуатируемых зданий и сооружений наиболее значимым из показателей ресурса является безопасный остаточный ресурс Тбо- Если по истечению безопасного ресурса ремонтно-восстановительные мероприятия по снижению риска аварии на объекте произведены не будут, то величина (Г_п - Тщ) является временем «дожития» объекта. В этот период жизни объекта его сопротивляемость непроектным воздействиям снижена и использование (Т_п - Хщ) ресурса может привести к аварии, а зна-

Расчет безопасного ресурса зданий и сооружений чит и к убыткам, которые будут несоизмеримо выше стоимости предупредительных мероприятий.

• -              Литература

  • 1.    Мельников А.П. К теории прогнозирования риска аварии объектов строительства// Вестник Южно-Уральского государственного университета. Серия «Строительство и архитектура». -Выпуск 1. — 2001.

  • 2.    Вентцель Е.С., Овчаров Л.А. Теория вероятностей. — М.: Наука, 1969.

• 4.    Попов ГТ, Бурак Л.Я. Техническая экспертиза жилых зданий старой застройки. 2-е изд., перераб. и доп. — Л.: Стройиздат, Ленингр. отд-ние, 1986.        .

• 5.    Болотин В.В. Ресурс машин и конструкций.—М.: Машиностроение, 1990.