Расчет бинарных дифракционных решеток с клином травления

Многопорядковые фазовые дифракционные решётки предназначены для преобразования падающей плоской волны в набор плоских волн (дифракционных порядков) с заданным соотношением энергии между ними. Многопорядковые дифракционные решётки широко применяются как делители пучка в устройствах оптической связи, обработки информации, в когерентных оптических процессорах, в волоконной оптике.

Бинарные дифракционные решётки представляют особый интерес ввиду простоты их изготовления методами литографии; бинарный рельеф формируется за одно травление подложки [1]. На стадии травления действуют факторы, искажающие бинарный профиль решетки. Основное искажение состоит в появлении так называемого клина травления. В первом приближении наличие клина травления состоит в замене вертикальных границ ступенек на наклонные (рис.1). В зависимости от типа травления положение клина травления может быть «внутренним» или «внешним» (рис.1). Возможно также введение коррекции в фотошаблон или процесс травления, обеспечивающей оптимальное положение клина травления по минимуму среднеквадратичной ошибки исходного бинарного профиля и профиля с клином травления (рис.1г).

теории

проанализирован характер ошибок, вы-

званных наличием клина травления, и проведен расчет многопорядковых бинарных решёток с учетом клина травления.

Расчет интенсивностей дифракционных порядков

В рамках скалярной теории интенсивности дифракционных порядков определяются как квадраты модулей коэффициентов Фурье в разложении функции комплексного пропускания решётки [1]:

I j

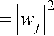
1 L V ( A ■ 2n ■ Ъ — exp i ф ( x ) - i — jx fix d о 4 d )

где ф ( x ) - фазовая функция решетки, X - длина волны, d - период решетки. Фазовая функция ф ( x ) определяется через высоту профиля решетки h ( x ) в виде:

ф ^{( x} ) = —⁽ n о X

- 1) h ( x ),

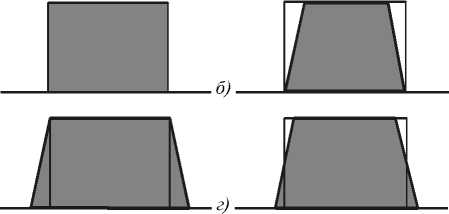
Рис. 1. Ступенька бинарной решетки:

а) без клина травления, б) с клином, характерным для жидкостного травления, в) с клином, характерным для ионно-лучевого травления,

г) с клином, обеспечивающим минимальную среднеквадратичную ошибку.

где n ₀ – показатель преломления материала решетки. Для бинарной решетки функция h(x) является кусочно-постоянной, принимающей значения 0, h _max . При учете клина травления функция h(x) становится кусочно-линейной. В частности, при наличии внешнего клина, функция h(x) имеет вид, приведенный на рис. 2, где x ₁,..., x _{2 K} – координаты штрихов исходной бинарной решетки без клина, K - число штрихов, а - угол, описывающий клин травления. В дальнейшем координаты штрихов x i , i = 1,2 K будем считать нормированными на величину периода.

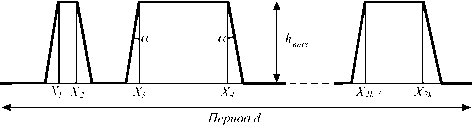
Рис. 2. Профиль бинарной решетки с «внешним» клином травления

Для расчета многопорядковых бинарных дифракционных решёток разработаны эффективные градиентные и итерационные процедуры [1-7]. Известные методы не учитывают наличие клина травления, свойственного литографической технологии. В данной работе в рамках скалярной

Для расчета интенсивностей дифракционных порядков I_j необходимо вычислить интегралы w_j в (1). Представляя интегралы в (1) в виде сумм по линейным и постоянным участкам профиля решетки, получим w_j в виде:

W j ( x ; ф , a , в ) = W j + Z S p , p = 1

j * 0, j = ± 1, ± 2, —

W o ( x ; Ф , a , в ) = W b 0 - 2 K Ax

(    exp( i ф ) ^- 1 )

xl 1                :                I,

V       iФ    J

где x = (x1,..., x2K) - вектор нормированных на период координат штрихов, ф = 2п(n0 -1)hmax / X - фаза ступеньки, в = d / X - размер периода относительно длины волны, A = hmax tg(a)/ d - нормированная ширина клина, i 2K

S 1 = — Z^{( - 1)} n ^exP^{( - 2 n} j^x n ) ^x

^{2 n} j n = 1                                              (4)

x|^ 1 - exp ( 2 n i ( - 1) ^{n + 1} j A ) ] ,

S 2 =

tg ( a ) ( ^exP ( ⁱ Ф ) ^{- ex}P ( ² n ij ^A ) ) ^{2 n} i p ( ( n o - 1 ) - jtg ( a )/ в )

K xZ exP ( 2njv2n-1), n=1

s 3 =

tg(a) (exP(iФ)- exP (-2niA)) 2niв  ((no -1) + jtg(a)/p)

K xZ exP (-2uijx 2 n).

n = 1

Значения w_bj в (6)-(8) являются коэффициентами Фурье для бинарной решетки без клина травления:

2 K wb0 =1 - (1- exP( i Ф» Z(-1) n xn, n=1

i

1 wb. =— (exP(iФ) - 1)x j2

r 2K     „)

^x l Z ^{( -} 1) ^exP^{( - 2 n ijX} n ) I , ^j * 0, ^j = ± 1, ± ^2, —

V n=1

Формулы (1), (3)-(7) позволяют рассчитывать интенсивности дифракционных порядков при наличии внешнего клина травления. Для клина травления другого типа (рис. 1) формулы получаются при очевидном изменении координат бинарных штрихов.

Следует отметить, что для бинарной решетки интенсивности порядков (1), (7) не зависят от величины периода. Для решеток с клином травления интенсивности порядков включают параметр в = d / X , определяющий величину периода в длинах волн.

Исследование и оптимизация профиля бинарных решеток с клином травления

С помощью формул (1), (3)-(7) было проведено исследование влияния клина травления на работу бинарных дифракционных решеток. Исследование про- водилось с выполнением трех следующих шагов. На первом шаге были рассчитаны бинарные дифракционные решетки для формирования различного числа порядков M=2N+1 равной интенсивности. Решетки были рассчитаны с помощью градиентного метода [1,2] минимизации квадратичной функции ошибки

N ₂