Расчет бинарных диэлектрических решеток и одномерных ДОЭ в рамках электромагнитной теории

Широкое использование дифракционных оптических элементов (ДОЭ) для фокусировки и преобразования волновых фронтов делает актуальным разработку эффективных процедур расчета ДОЭ в рамках точной электромагнитной теории. Требования к компактности и эффективности оптических устройств приводят к необходимости расчета ДОЭ с малыми зонами рельефа порядка нескольких длин волн. Это делает невозможным использование известных итерационных и градиентных алгоритмов, разработанных для скалярного приближения Кирхгофа [1,2].

Особый интерес представляет электромагнитный расчет многопорядковых дифракционных решеток. Это связано как с широким использованием решеток в качестве светоделительных и мультиплицирующих элементов в устройствах оптических вычислений и связи, так и с представлением сложных ДОЭ в виде решеток с переменным шагом и ориентацией штрихов [3,4]. Представления ДОЭ в виде суперпозиции решеток позволяют расчет и анализ работы ДОЭ свести к набору задач расчета дифракционных решеток. В частности, в работах [5,6] расчет ДОЭ сводится к расчету решеток, концентрирующих излучение в 1-ом порядке, а в работе [7] – к расчету решеток с заданной фазой нулевого порядка.

В данной работе рассмотрен градиентный метод расчета бинарных диэлектрических решеток в рамках электромагнитной теории. Метод состоит в итерационном расчете бинарного профиля периода из условия формирования заданной интенсивности порядков. Метод применен к расчету бинарных однопорядковых решеток, концентрирующих излучение в одном порядке. На примере линз рассмотрена возможность использования таких решеток для расчета высокоэффективных бинарных ДОЭ.

где k=2 n/X, X - длина волны, на диэлектрической бинарной решетке, имеющей на периоде [ 0,d ] K штрихов с координатами x ₁ ,..., x _{2 K} . Геометрия задачи дифракции приведена на Рис.1, где R_n и T_n -коэффициенты отражения и пропускания дифракционных порядков. Для приведенной геометрии задачи имеются три зоны с различной диэлектрической проницаемостью е . В зонах 1 и 3, то есть при y > a, где a –высота штрихов решетки и при y <0, диэлектрическая проницаемость постоянна. Без ограничения общности будем считать, что в первой зоне е =1, а в третьей зоне £ >1 . Во второй зоне y е [0, a ] - зоне модуляции, диэлектрическая проницаемость является функцией £ = e (x) .

Рис.1. Геометрия задачи дифракции на бинарной диэлектрической решетке.

Рассмотрим дифракцию двух независимых ТЕ и ТМ поляризованных плоских волн. В первой (y> a ) и третьей зонах (y<0) поле соответствует разложению Рэлея. При y> a поле имеет вид [8]

u ( x , У ) = exp ( i ( а о ^х — в о У )) +

⁺ Е R n ^e xp ⁽ i “ n x ⁺ Р п У )) , n =-^

где

I an = к о sin(^)+ n 2^-, k 02 = to 2 / c2 = (2n / Xo )2, j _________ d

\pn=V k 02 — a2

а скалярная функция u(x,y) соответствует компоненте Еz(x,y) электрического поля для ТЕ-поляризации и компоненте Hz(x,y) магнитного поля для ТМ-поляризации. При y<0 поле имеет вид [8]

да                z Z

~ х,У) = LTn exP(i(anx — РпУ

n =—да

~       ,2      2

где Pn kkо £ an .

Разложения Релея (1), (3) являются решениями уравнения Гельмгольца

A u + к ² и = 0,

22 22

при к = к q и к = к q £ , соответственно. В зоне модуляции (при у е [0, a ]) поле описывается системой дифференциальных уравнений, различных для случаев ТЕ и ТМ поляризаций. В дальнейшем будет рассмотрен только случай ТМ поляризации.

Для случая ТЕ поляризации выкладки аналогичны. Для ТМ-поляризации функция H z (x,y) ищется из решения следующей системы уравнений [8]

' ~ H        = к 2 E( х, y), aEх, у)_ а Г1 aHz (x, у))/

=I                 I — H -\X ду       дх (к2    дх)

.    (5)

, у )

_c ² K( a j    ( П   )

S n = L ^(— 1 ) j ^ex p |^— i , ^nx j I , j = 1            ^l d       -

2 K

Q = L(— 1)jxj j=1

Таким образом, в зонах 1 и 3 решения имеют вид

• (1)    и (3), а в зоне модуляции для поиска решения необходимо решать систему (7). Для поиска общего решения системы (7) необходимо найти 4N+2 ли-

• нейно-независимых частных решений. При отсутствии модуляции (£(х) = £) базисные решения систе-
• мы (7) имеют вид:

^H ± ⁽ у ) = ^exP ⁽± i ^e p У ). p = ^{— N} , ^N , <  ~ ±.      i p p     / ~ x ----- (10)

Ep(у)=± — exP(±iPpУ). p = — N,N к о £

Для согласования решения в зоне модуляции 2 с решением (10) в зоне 3, граничные условия для системы (7) определим в виде:

J H T mj ( 0 ) = 3 m    m , j = — N , N

~T          ~                            ,

[ E mj ^{( q )} = + i P m ³ m — j ^{/ ( к} 0 ^£ j ^m , ^j = ^{— N} , ^N

Функции H z ( х , у ) и E_х ( х , у ) в (5) являются ква-зипериодическими [8];

H z ^{( х} , у ) = L H m ⁽ у ^{) eX} P ^{( i a} m ^x )

_с              m =—да                                    (6)

E х ^{( х} , у ) = L E m ⁽ у ^{) ex} P ^{( i a} m ^x )

m =—да

где 5 _m

1, m = 0, 0, m * 0

Для удобства выкладок введем 4N+2 объединён-

ных векторов начальных условий вида

ГГ H + N ^{( 0 )}I  f H N ⁽ °M H ^— N ^{( 0 )}I

(( E — N ( 0 ) )"l E N ( 0 ) J\ E — N ( 0 ) J

^f H N ( 0 )

I E N ( 0 ) JJ

В дальнейшем будем считать, что функции E_х ( х , у ) , H z ( х , у ) в зоне модуляции могут быть

Обозначим T i ( у ), i = 1,4 N + 2 вектора базисных

аппроксимированы отрезками своих рядов (6) с 2N+1 членами. Подставляя (6) в (5) и разлагая функции к ² ( х ) = к 2 ■ £ ( х ) и 1/ к ² ( х ) в ряды Фурье,

функций ffT — N (у ))

Il T — N ( у ) ) ’

f ^T N ⁽ у ) I l T N ( у ) )

получим, при учете 2N+1 членов в (6), следующую

' ^T N ⁽ у ) I ^{f T} N ⁽ у ) I

систему 4N+2 дифференциальных уравнений с по

стоянными коэффициентами:

l T — N ( у )7"’ l T N ( у ) JJ

' dH p ⁽ у ) dy ^dE p ⁽ у ) dy "

1 = L E1 (у )c Р1—i, p = — N, N, l=—N

N

= ^a p L ^a i c p — i ^H i ⁽ у ^)— H p ⁽ у )

1 =— N

.

p = — N, N где c?, сП2^ - коэффициенты Фурье;

c ( 1 )=J cn

'^к 0 ^{( £} — 1) n

--S „, n * 0

n

2n к2 + kfc—l) ■ Q, n = o’

d

c

( 2 )      2 n nk 2

' П = 1       „ ।

■ S_n ,        n * 0

1/ к ₀ ² +

,

■ Q , n = о к ₀ ² d

полученные из решения системы (7) с начальными условиями (12). При этом общее решение системы принимает вид

N

H m ( у ) = L C ^— j Y mj ( у ) + j =— N

N

+ L C+j Ymj (у), m = — N, N, j=—N

N

E m ( у ) = L C j Y mj ( у ) + j =— N N

+ L C ⁺ j Y mj ( у ), m = — N , N .

j =— N

Для определения коэффициентов пропускания T n и отражения R _n в (1), (3) воспользуемся условиями непрерывности поля H z ( х , у ) и функции Е_х ( х , у ) на границах зоны модуляции при у=0 и при y=a . В результате получим

T = 2 exp ( - i p o a ) ( h 01 - D _p ■ H_n ) ^{- 1} ■ 6 ,       (16)

R = H — 1 H 11 ■ T + exp ( - 2 i P ₀ a ) ■ 6 ,            (17)

где t_n

cosfe )

7 e cos ( ^ )

для ТМ – поляризации, а углы

где матрицы H₀₁ , H 11 , H₁₂ , D _p имеют вид

~

O n соответствуют направлениям прошедших волн

H 01 pj = * рЛ a ), H 11 pj = * pj ( a ) iPp

H 12 pj = 5 p - j ■ ^ exp( i p p a ),              (18)

k 0 ²

D p pj = ⁸ p - j ■ k О / i P p , p , j = — NN , а 8 - вектор столбец, центральный элемент которого равен единице, а остальные элементы равны нулю.

Решение системы дифференциальных уравнений (7) с постоянными коэффициентами с граничным условием X ₀ может быть записано в компактном

в уравнении (3).

Для построения градиентной процедуры расчета профиля дифракционной решетки введем некоторую функцию ошибки e ( p ) , характеризующую от-

личие рассчитанных значений интенсивности I _n в дифракционных порядках от требуемых значений I n :

^{e (} p ) = ^{e ( 1 (} р ) , I ) ,                                    ⁽²⁵⁾

где p = ( Х 1 ,..., x 2 к ) - вектор координат штрихов ре-

матричном виде;

шетки, K - число штрихов на периоде, I = ( I n ) Mm ,i = ( ~ n ) - М , - вектора рассчитанных и

f ^v p ⁽ У ) 1 V ~ p ( У ) )

= exp ( A ^TM

■ y ) X o

где

A TM = f NU F 1 1

V F₂ NU )

требуемых значений интенсивности в порядках.

Градиентная процедура минимизации функции ошибки e ( p ) состоит в итерационной коррекции параметров профиля решетки по правилу:

p n + 1 = p n ^- t ■V ^{e (} p ^{)                           (26)}

матрица системы (7). В уравнении (20) NU – нулевые матрицы, а F 1 , F 2 – матрицы из Фурье коэффи-

где n - номер итерации, t -шаг градиентного алгоритма. Рассмотрим вычисление градиента функции ошибки V e ( p ) для случая ТМ поляризации. Соглас-

циентов:

F¹ i , j = c i ^- j ’ F ² i , j =

de ( p )

но (25) частные производные имеют

вид:

= ^а - ( N + 1 ) + i ^a - ( N + 1 ) + j c i - j ^{- 8} i - j ,

5e ⁽ p) _

i , j = 1,2 N + 1

m

(

Матричное представление (19) позволяет компактно выразить матрицы H ₀₁ и H ₁₁ в (16), (17) через матрицу системы и граничные условия (12) в виде:

[ H ⁰¹ 1 = exp ( A ^TM ■ a ) ■ BC ,                  (22)

V ^H 11 )

м Z j =- M

м

= 2Re Z

где матрица BC составлена из второй половины векторов начальных условий в (12);

BC =

^H - N ( ° ) 1 . E - N ( 0 ) )

,...,

f H N ( ⁰ )

V E N ( 0 ),

E

DE

где E – единичная матрица, а DE – диагональная матрица с элементами - i p j I k 0 e , j = - N , N .

3. Градиентный метод

В данном пункте рассмотрен градиентный метод решения обратной задачи расчета бинарной диэлектрической решетки. Метод состоит в расчете координат штрихов ( X 1 ,..., x 2 к ) профиля решетки (см. Рис. 1) из условия формирования заданных интенсивносте й       дифракционных       порядков

I n , n = - M , M , соответствующих прошедшим волнам в уравнении (3). Интенсивности дифракционных порядков пропорциональны квадратам модулей коэффициентов пропускания T n в (3);

I n = t n ■ Tn I²                                       (24)

xm de(l, I) 5!j (p) =

^ I j

^d j

xm t T»^Tj(p)'' j j dxm ?

Уравнение (27) удобно представить в виде реальной части скалярного произведения

^£(2) = 2Ref ^TM dxm       V dxm векторов dT(p). f ^Tj (p) 1M

m

^m ) - M

и

L = ( L ^ M , L. j - MM ’     j

,

M

Z j=- M

д^ T tjj.

^ I j

Вектор производных d T ( p ) I d x m чить из (16) в виде;

д Т       д , . z x

-— = -— (2 ■ exp(- iP 0 a)x дxm   дxm

несложно полу-

^{x( H}01

-I

D e ■ H 11 ) ^- 1 ■ б ) =

-

^De ■

1 [ д Н о1

V ^д x m

-

^D e ■

д Н 11 I T

I ^д x m )

Для расчета производных d H 01 1 д x m , д Нц / д x m продифференцируем уравнение (22):

Р^Н oi )

— д x m дНп	= 5T( exp ( A™ ■ а ) - Вс ) = д x m
l xm 7

I n '

д F ₂

t— = « ^_( N + 1 ) + i « ^_( N + 1 ) + j ^д x m

0c(2) дcl - j дxm

д f

д x

m l n = 1

f — (a TM )

Ь n! V ’

( . \ _m ( 1/ е - 1 )

= a-(N+1)+1a-(N+1)+j' (- 1) ----2----х k02d

■ BC =

да n

у a—д

l Ь1 n дXm

I n '

■ BC .

При суммировании ряда в уравнении (31) произ-

водные

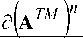
^д x m

следует вычислять с использова-

нием рекуррентной формулы:

^д ( a тм ) ⁿ = a тм ■ ^д ( a тм ) ^{n - 1}

д x m                д x m

+ ^-4 тм ) ^{n - 1}

xm

При этом расчет производных матриц H 01 и H 11 по порядку сложности эквивалентен вычислению экспоненты в степени матрицы через ряд. Для расчета производной д А TM I д x m воспользуемся пред-

ставлением матрицы ATM в уравнении (20). Диф- ференцируя (20), получим f х .    дF1 ) я a tm NU ----- =       иxm , дxm      2 NU (33) ах l xm       7 где NU – нулевые матрицы, а матрицы дFi I дxm, i = 1,2 могут быть получены из (21) в ви-

х exp |- i 2 ^ ( 1 - j ) x m | , 1 , j = 1,2 N + 1 l d 7

Таким образом, компоненты вектора градиента функции ошибки имеют вид реальной части скаляр-

ного произведения:

^^pL 2Re((H01 -Dp ■ Hu)-1 х дxm f    dH11 dH 01

х I D о l    дxm   дxm

где вектор T определен уравнением (16), вектор L определен уравнением (29), матрицы H 01 и H 11 аналитически выражаются через матрицу системы (7) и граничные условия (12) в виде (22), а матрицы производных д Н 01 1 д x_m , д Нц I д x_m определены в уравнениях (31)-(34).

Высота профиля решетки a также может рассматриваться как параметр оптимизации. Производная функции ошибки по параметру a также имеет вид (36), где матрицы д Н 01 1 д a , д Нц / д а могут быть

получены из (22) в виде

^f^ H 01 '

яда = —(ехр(АTM ■ а)■ BC дН11    да            ’ l д a J

= A TM ■ exp ( A TM ■ а ) ■ BC

Отметим, что для случая ТЕ поляризации вычисле-

де:

dFi = дc     =(_ 1) m k 02 (е -1) х дxm   дxm            d х exp|- i П (1 - j)xm |, 1, j = 1,2N +1

l d 7

ния аналогичны, при этом компоненты градиента также имеют вид (36), (37), где матрицы H 01 и H 11 выражаются через матричную экспоненту.

Таблица 1. Результаты градиентного расчета бинарных диэлектрических решеток в электромагнитном приближении ( d =5.5 Я₀, £ =2.25, 6 =0).

Число порядков M	Число штрихов К	Высота штрихов ( a / λ 0 )	Координаты профиля	E (%)	δ (%)
ТМ-поля			ризация
5	2	0.9	(0.1820, 0.4822), (0.5544, 0.8546)	80.1	3.1
7	2	0.9	(0.2454, 0.4367), (0.5999, 0.7912)	85.1	1.0
9	3	1.56	(0.0925, 0.1963), (0.3728, 0.4786), (0.6155, 0.7185)	96.1	0.6
11	3	1.6	(0.1515, 0.3435), (0.4845, 0.5753), (0.7162, 0.9046)	94.0	5.1
ТЕ-поляризация
5	2	0.8	(0.1798, 0.4816), (0.5550, 0.8567)	80.7	2.5

7	2	0.875	(0.2579, 0.4297), (0.6070, 0.7787)	83.8	1.1
9	3	1.0	(0.0091, 0.1924), (0.3145, 0.4811), (0.7769, 0.9547)	89.7	3.6
11	3	1.57	(0.0444, 0.3390), (0.5033, 0.5567), (0.8259, 0.8792)	91.5	4.3

• 3.    Результаты расчетов решеток

Разработанный градиентный метод был применен к расчету бинарных диэлектрических решеток ( ε =2.25) решеток для формирования M =2 N +1 равных порядков. В качестве функции невязки была использована квадратичная функция ошибки

N       _~²

^{e (} P ) = ZV I j ( p ) ^- I j ) .                          ⁽³⁸⁾

j =- N

Для характеристики работы решеток были использованы значения энергетической эффективности

N

E ( M ) = Z I j j =— N

^ ( M ) = 1=

¹ N ( IJ ^M j ^Z N

где I = E ( M ) / M - среднее значение.

Результаты расчетов решеток при нормальном падении ( 0 =0) и периоде d =5.5^ 0 . приведены в таблице 1. Следует отметить, что при указанных параметрах решетки расчет в рамках скалярного приближения дает недопустимо высокую ошибку δ ~100% [9]. Данные таблицы 1 показывают, что использование градиентной процедуры в рамках электромагнитной теории позволяет снизить среднеквадратичную ошибку δ до 1-4% при энергетической эффективности 80-94%.

и среднеквадратичной ошибки формирования заданной равной интенсивности порядков

Таблица 2. Результаты градиентного расчета бинарных дефлекторов, концентрирующих излучение в -1-ом порядке ( £ =2.25, 0 =0, ТЕ поляризация).

Период (d/λ0) Число штрихов К Высота штрихов (a/λ0) Координаты профиля E (%) 3.5 2 1.68 (0.2596, 0.4378, 0.6082, 0.6754, 0.8469, 0.8780) 83.5 4.5 4 1.69 (0.2617, 0.4009, 0.5426, 0.6043, 0.7001, 0.7361, 0.8521, 0.8734) 87.7 5.5 5 1.78 (0.2714, 0.3982, 0.4997, 0.5565, 0.6100, 0.6473, 0.7243, 0.7560, 0.8793, 0.8984) 87.6 6.5 5 1.5 (0.1809, 0.4334, 0.4717, 0.5302, 0.6113, 0.6530, 0.7566, 0.7845, 0.8997, 0.9142) 80.0 ляризации. В качестве функции ошибки была использована квадратичная функция ошибки

е ( PM ^{1 -} I - 1 ⁽ Р ^{)) 2} ^ min.

Таблица 2 показывает, что в –1-ом порядке можно собрать более 80% энергии и при «больших» периодах. При этом для достижения высокой (>80%) эффективности на периоде d=p λ 0 необходимо порядка p штрихов.

• 4.    Синтез ДОЭ на основе однопорядковых решеток

Решетки, позволяющие сконцентрировать излучение в –1-ом порядке, имеют большое практиче- ское значение. Рассмотрим возможность использования подобных решеток для расчета различных фокусирующих ДОЭ, например линз. В скалярном приближении для расчета ДОЭ обычно используется приближение тонкого оптического элемента, описывающее ДОЭ через фазовую функцию. Пусть p(x ), X G [о,d ] - фазовая функция ДОЭ, рассчитанная в приближении геометрической оптики из условия фокусировки в заданную область. Приближение геометрической оптики основывается на уравнении наклонов, определяющем направление преломленного луча через фазовую функцию ДОЭ в

виде

Sin9 )_  ‘ fd^fx) + dpAA k0 V? V dx dx

_ Х f d p ( x ) ₊ d p о ( x ) ^ 2 n V dx dx 7

бинарной отражающей линзы, имеющей для случая ТЕ поляризации эффективность ~90%.

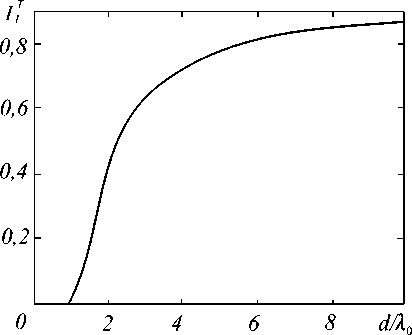
Рис. 2. Интенсивность 1-го порядка правой пилообразной решетки в зависимости от длины периода для ТЕ-поляризации при £ =2.25, 9 =0 и высоте профиля a _ Х _о / (V ? — 1 ) .

где Х _ Х о / V ? - длина волны в среде, Р о ( x ) _ k о sin ( 9 ) ■ x - фазовая функция освещающего пучка при y=0 . Уравнение (42) совпадает с уравнением решетки

V ? ■ sin ( e m ) _ sin ( 9 ) + m X ₀ / d

при периоде d _ 2 n /

d p ( x ) dx

и m _ ± 1. Знак m опре-

деляется

. f d p ( x ) ) m _ sign I

V dx )

знаком производной

фазы;

. Данное значение периода совпа-

дает с размером зоны ДОЭ A x , определяемой из

условия

A p ( x ) _ 2 п - d P < x >

dx

A x ^

^ A x _ 2 п /

d p ( x ) dx

.

Таким образом, приближение геометрической оптики предполагает, что каждая зона ДОЭ работает как «однопорядковая решетка», концентрирующая излучение в –1-ом или +1-ом порядке. В скалярном приближении Кирхгофа однопорядковой решетке соответствуют левая или правая пилообразная решетка. При малых зонах геометрооптическое и скалярное приближения неработоспособны, поскольку неработоспособной оказывается пилообразная решетка. В частности, для правой пилообразной решетки с высотой a _ Х о / (V ? - 1 ) интенсивность 1-го порядка стремится к нулю при d ^ Х о (см. Рис.2). Можно предположить, что при замене зон ДОЭ бинарными решетками, рассчитанными в электромагнитном приближении из условия максимизации -1го или 1-го порядка, получится высокоэффективный бинарный ДОЭ. Хотя формулы (42), (43) являться лишь эвристическим обоснованием метода замены зон ДОЭ «однопорядковой» решеткой, на практике метод оказывается работоспособным. В частности, в работе [5] рассмотрен расчет внеосевого сегмента

Расчет линзы в [5] основывался на замене зон непрерывной дифракционной линзы простейшей отражающей бинарной решеткой с одним штрихом. Для ТЕ-поляризации при d ~ λ 0 , θ ~30⁰ и высоте₍ штриха a ~0.25 λ ₀ такая решетка концентрирует из-

лучение в –1 порядке [5].

Проиллюстрируем работоспособность метода на примере расчета преломляющей линзы. Фазовая функция дифракционной линзы имеет вид

p ( x ) _ mod 2„ I — ( - x sin ( 9 ) V Х о^

^- ? ^{( x - x} о ^{) 2 +} f ^{2 +} c

-

где ( x₀f ) - координаты фокуса. При d=20 X _о, 9 =3о^о и ( x₀,f)=(-20 X ,-85 Х о ) фазовая функция линзы имеет 2о зон с размером о.89 Х о < A x <  1.17 Х о . Для расчета

бинарной линзы требуется записать в зонах линзы бинарную решетку, имеющую максимум в –1-ом порядке. При 9 =3о^о и A x ~ Х о достаточно простей-

шей бинарной решетки с одним штрихом

h 2 ^{( x )_}

о, x е [ о, A x /2 ) a ■ Х о , x е [ A x /2, A x )

В частности, для ТМ поляризации и £ =2.25 решетка (45) концентрирует излучение в –1 порядке при высоте штриха a~ 2 λ 0 [10]. На Рис. 3 и 4а) приведены рассчитанный бинарный рельеф линзы и распределение интенсивности

I ( x , f ) _ |Re ( ^ x ( x , f ) ■ H * ( x , f ) ) _

1 ^f ^  ~           ~

^_^ ^Im   E T n P n ■ ^ex P ^{( i} \ ^an ^{x -} P n f ))

^k о ^£

VV n _- N

X

*

N           ~

E T n exp ^{( i (} « n ^x - P n f ))

V n _- N

7 7

в фокальной плоскости у=-85 Х _о при N =57.

X (46)

a/X„ "

1,8 -

О

1.6 -

1,4 ■

1.2-

0,8 ■

0.6 ■

0.4 -

0,2 ■

х/Х,

Рис. 3. Бинарная линза с апертурой d=20 X 0 для фокусировки точку ( х₀ , f)=( -20 X 0 ,-85 X о ) при 9 =30 0 , £ =2.25.

i(x,.D

6 - h (x )=     V£ - sin(g)     x

£ - cos ( 0)4£ - sin ( 0 )

x mod Яд | c - x sin(0)- £(x (x - x о )2 + f 2 |, x е [О, d ]

рассчитанным в приближении тонкого оптического элемента.

Распределение интенсивности на Рис. 4б) оказывается размазанным в отличие от острого пика с шириной 5 X 0 , сформированного бинарной линзой. Простейшая решетка (45) с одной ступенькой может быть использована только при угле падения 0 ~ 3О^О и при размерах зон близких к длине волны. Большие, по сравнению с длиной волны зоны, требуют более сложных решеток с несколькими штрихами. При этом актуален расчет однопорядковых решеток для некоторого интервала периодов [ d min , d _max ] , определяющего изменение размера зон ДОЭ. Расчет бинарной решетки с максимальной интенсивностью I — i ( p , d ) в -1-ом порядке при d е [ d min , d _max ] может быть проведен рассмотренным градиентным методом с функцией ошибки определенной, например, в виде

4 -

£ p ) = J ^d max ( 1 - 1 — 1 ( p , ^ )) ² d ^ ^ min , ^d min

2 -

о

а)

Ox,t)

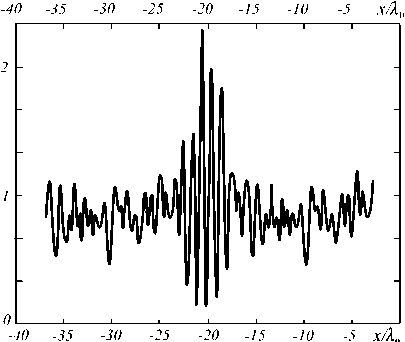
б)

Рис. 4. Распределения интенсивности в фокальной плоскости (при y= -85 X 0 ) (а) для бинарной линзы на рис. 3, (б) для непрерывной линзы (47) для ТМ -поляризации.

Указанное выражение для интенсивности I ( x , f ) пропорционально у -компоненте вектора Умова-Пойнтинга. Для сравнения на Рис. 4б) приведено распределение интенсивности для линзы с непрерывным рельефом

где р – вектор координат штрихов решетки. Приведем пример расчета сложной бинарной линзы с большими зонами и большим интервалом изменения размеров зон. При размере апертуры d =30 Я о , координатах точки фокусировки ( x ₀ f )=( 0,-130 X 0 ), угле падения 0 =10⁰ и £ =2.25 линза с непрерывным рельефом (47) имеет 10 полных зон с размером от 5 Я о в начале апертуры до 2 X 0 на краю апертуры. Для расчета бинарной линзы требуется рассчитать решетку из условия максимума интенсивности в –1-ом порядке для интервала периодов [2 X 0 , 5 Я о ]. Градиентным методом для случая ТМ-поляризации была рассчитана решетка с тремя штрихами из условия максимума –1-го порядка для указанного интервала периодов при функции ошибки (48). Нормированные на период координаты штрихов решетки равны p =(0.0429, 0.2981, 0.4556, 0.5771, 0.7745, 0.8276) при высоте штрихов a=2.07 X 0 . Данная решетка при d е [ 2 Я о ,5 Я о ] концентрирует в -1-ом порядке не менее 80% энергии.

На Рис.5а) приведен профиль бинарной линзы, полученный заменой зон линзы (47) рассчитанной бинарной решеткой, а на Рис. 5б) – распределение интенсивности, сформированное бинарной линзой при у = -130 Я о .

Для сравнения на Рис. 5а), 5б) также показаны профиль непрерывной дифракционной линзы (47) и распределение интенсивности

£           £ ^£     I

I ( x , f ) =---- [ exp - 2m----xu I du

X ₀ f ^J           л f I

V

Я о f

(Гл 2 П£ ■ d

d ² V £

Sinc Я о f

V Я о f

где Sinc ( x ) = sin ( x ) / x , формируемое в скалярном приближении Кирхгофа в фокальной плоскости идеального сферического фронта.

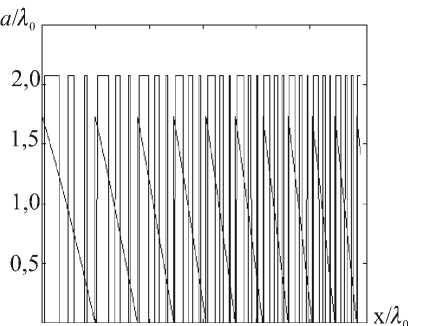
а)

б)

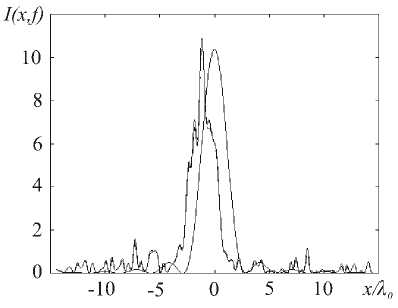
Рис. 5. а) Бинарная линза (d=30 X ° ) для фокусировки в точку ( x₀ , f )=( 0,-130 X ° ) при 9 =10°, £ =2.25 и непрерывная линза (47), б) Распределение интенсивности, сформированное бинарной линзой для ТМ – поляризации и распределение интенсивности при идеальном сферическом фронте.

Рисунок 5 показывает хорошую работоспособность рассчитанной бинарной линзы и демонстрирует возможность замены задачи расчета ДОЭ су-

щественно более простой задачей расчета однопорядковой решетки также и при большом диапазоне изменения размеров зон.