Расчет четной симметричной бинарной решетки для генерации заданного набора дифракционных порядков

Расчету многопорядковых дифракционных решеток посвящено большое число работ.

В большинстве из них для проектирования решеток используются четыре метода: метод перебора решений Дамманна [1-3, 7], итерационный метод Ньютона решения системы нелинейных алгебраических уравнений [4-6, 8], итерационный метод Герч-берга-Секстона [9,10] и градиентный метод [11-13].

Метод перебора решений (метод Дамманна-(МД)) наиболее прост при формировании четного и действительного распределения интенсивности по порядкам. В случае, если заданы интенсивности порядков, то фазы их должны быть равны только нулю или π . Перебором из 2 ^N возможностей, где M=2N+1 число порядков дифракции, можно выбрать решение для бинарного профиля четной решетки с максимальной дифракционной эффективностью. При этом каждый раз, при определенном выборе фаз дифракционных порядков, решается нелинейная система алгебраических уравнений.

Если период рельефа бинарной решетки не является четной функцией , то фазы половины порядков дифракции могут иметь любые значения, и метод перебора не работает. Метод Ньютона (МН)[4-6,8] решения нелинейной системы алгебраических уравнений пригоден для любой функции, описывающей профиль бинарной решетки. Его особенность в том, что он дает точное решение задачи (либо не имеет решения) выравнивания интенсивности M порядков, но не позволяет контролировать значения интенсивности других порядков, не подлежащих выравниванию. Это приводи к низкой дифракционной эффективности решетки. Если не подлежащие выравниванию порядки ввести в число заданных, приняв значения интенсивности у них равным нулю, то это увеличит размерность нелинейной системы уравнений. При этом увеличивается не только объем затрат времени и ресурсов компьютера, но и вероятность не существования решения системы. В наших экспериментах МН надежно работал до числа порядков равного M=21.

Итерационные методы (ИМ) Герчберга-Секстона и его модернизация [9,10] с бинаризацией решения на каждом шаге итераций не позволяют достичь высоких точности и эффективности при выравнивании интенсивности по порядкам. Эти методы предназначены для расчета многоуровневых фазовых решеток.

Градиентный метод (ГМ) (сопряженный или наискорейшего спуска) [11-13] позволяет достичь высокой дифракционной эффективности и малой (но не нулевой) ошибки выравнивания порядков. Наи- более успешно ГМ сходится при выборе аналитического геометрооптического начального приближения [11]. Если начинать итерации ГМ со случайного распределения скачков фазы бинарного рельефа решетки, то нельзя добиться малой ошибки выравнивания интенсивности порядков. ГМ и ИМ включают в рассмотрение все порядки ( подлежащие выравниванию и подлежащие обнулению), что не существенно влияет на их работоспособность в отличие от МН.

В данной работе на примере четной бинарной фазовой решетки показано, что начиная со случайной фазы решетки и с ГМ и включая последовательно МН, можно достичь лучшего результата выравнивания интенсивности порядков, чем применяя перебор решений Дамманна.

Рассматриваемый алгоритм назван гибридным итерационным методом (ГИМ). При этом по МД требуется для каждого выбора фаз провести несколько (пусть L) итераций МН и всего 2 ^N L итераций , а ГИМ требует выполнения примерно 2L итераций, где M=2N+1 число порядков, подлежащих выравниванию.

• 2.    Бинарная решетка Дамманна

0.5 _~

На рис.1 показана оптическая схема использования дифракционной многопорядковой решетки . Следуя методу Дамманна [1] периодическая двухфазная решеточная функция P(u) может быть представлена математически как

P ( u ) = P ^~ ( u ) ∗ comb ( u ) ,                         (1)

где P~(u) это один период решеточной функции, ∞ comb(u) = ∑δ(u - n) . Период свертки такой же. n=-∞

Отклик решетки, это обратное Фурье преобразование, можно представить как ∞

p ( x ) = ∑ ^~ p ( n ) δ ( x - n ) ,                        (2)

n = -∞ где

^~ p ( n ) = ∫ P ( u ) exp( j 2 nuπ ) du .                  (3)

• - 0.5

  
  
  
  

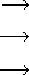
  фазовая решетка. P(u)

  
  

^ отклик решетки р(х)

Рис.1. Периодическая фазовая решётка генерирует распределение точечных источников.

Функция решетки P ^{~ ( e )} ( u ) , представленная на рис. 1, имеет четное число нулей 2 N_z

^~ p ( n ) с комплексной амплитудой порядков q(n) с

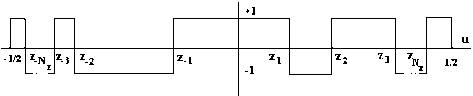
Рис.2 Бинарный профиль одного периода фазовой решетки и представлена математически как

P⁽ e ) ( u ) = ( - 1) N Z rect ( u ) -

помощью константы а :

Р ( n ) = q ( n ) а , n = [ - N , N ] .                      (7)

Начальный массив q(n) точно определен на ограниченном диапазоне, тогда как решеточный отклик ^~ p ( n ) имеет бесконечную протяженность.

Дифракционная эффективность n определяется

N z

- 2 У (-1) krect k=1

^{( z} k + ^z - k )

^z k ^{- z} - k

Параметры z _k показывают расположение изменений фазы и называются нулями решетки. Из выражения (3) получаем отклик решетки:

^р e ) ( n) = ( - 1) N Z sin c ( n ) -

NZ

- 2 У ( - 1) k ( Z k - z- k )sin c [ ( Z k - z__k ) n ^] exp jn ( Z k + z__k ) ^{n ]} = k = 1

= ( - 1) N Z sin c ( n ) -                                     (5)

NZ

- 2 Z ( - 1) k {[ z k sin c (2 z k n ) - z - k sin c (2 z _ k n ) ] + k = 1

⁺ j ^{[ z} k ^{cos c (2 z} k n ) ^{- z} - k co c ^{2 z} - k ^{n ]}

как отношение входной энергии в области порядков, подлежащих выравниванию, ко всей энергии: NN

У| p(n )|2     У|р(n )|2     N n = n=-N-----= n ==-N 2 = Ур (n )|2.   (8)

И Р ( n ) 2   °f| P ( u ) du ⁿ =^- N

n

- 0.5

Для получения конечного выражения использована теорема Парсеваля и предположение, что T)(u) только фазовая функция: P(u)| = 1. Ди-

фракционная эффективность это сумма энергии в области источников. Мера ошибки показывает распределение энергии внутри этой области, по сравнению с требуемым распределением комплексной амплитуды:

N

E coh = У n =- N

^~ p ( n )

a

^- q ^{( n} )

, . sin( n )        , . 1 - cos( n )

где sin c(x) =--------, cos c(x) = nxnx

Если структура симметричная, то есть, если zk = -z-k , выражение (5) можно упростить:

~ e ^{( n} ) = ^{( - 1)} N Z ^{sin c ( n} ) ^-

NZ                         .(6)

- 2 У(-1) k 2 zk sinc(2 zkn)

k = 1

Индекс coh показывает, что выражением (7) связываются амплитуды и фазы, поэтому задача линейная по амплитуде и происходит сравнение комплексных амплитуд, хотя сама система алгебраических уравнений относительно координат скачков фазы решетки нелинейная. Если энергия сигнала представить в виде:

N

~~ = У q ⁽ n )|²,                                   ⁽¹⁰⁾

n =- N

тогда отношение сигнал-шум (SNR) можно запи-

сать:

Для четной решетки число нулей такое же, но число независимых нулей уменьшается на половину. Заметим что, так как P ^{~ ( e )} ( u ) реальная, ее от-

SNR

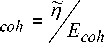
В случае некогерентного (нелинейного по амплитуде ) расчета фазы заданных порядков произ-

клик - эрмитова функция, такая что реальная компонента отклика четная, а мнимая нечетная, или амплитуда отклика решетки четная, а ее фаза нечетная. Если P ^{~ ( e )} ( u ) реальная и четная функция, то отклик - реальная и четная функция. Поэтому фазы порядков дифракции для четной фазовой решетки могут принимать только два значения : 0 и п .

вольны:

I p ^{( n} )l = q ^{( n} ) ^a , ⁿ = ^{[- N} , ^N ]

Мера ошибки в этом случае основана на разности интенсивностей:

3. Расчет профиля решетки

В этом разделе рассмотрен расчет одномерных бинарных решеток, формирующих заданное число порядков с одинаковой интенсивностью. Начальный массив порядков дифракции обозначим как q(n). Из-за невозможности предсказать абсолютную амплитуду отклика, необходимо установить связь отклика

N

Ein с = У inc n=-N

^~ p ( n ) ²

I ^{a 2}

- q ( n )|2

а отношение сигнал-шум будет в виде:

SNR inc

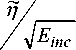
Введём так же среднеквадратичную относительную ошибку выравнивания интенсивности порядков, как это сделано в [11]:

5 = I

I

'

M

V

N

n =- N

1 1² 1 ² ,

где

N

I = — УЛ, , M=2N+1 . M n ^Z N ^,

Метод Дамманна , основан на решении нелинейной системы алгебраических уравнений (7), связывающих координаты точек скачков фазы решетки и комплексной амплитуды порядков дифракции, интенсивности которых задаются, а фазы выбираются произвольно из двух чисел: 0 и п . В МД число неизвестных решеточных параметров (число скачков фазы решетки на половине отрезка задания периода решетки) и полного числа амплитуд дифракционных порядков , подлежащих выравниванию, равны между собой. Для когерентного случая 2N+1 порядков дифракции соответствуют 4N+2 начальным параметрам , 2N+1 амплитуд и 2N+1 фаз. Следовательно, можно определить 4N+2 решеточных параметров. МД находит их, используя 4N+2 нелинейных уравнения. Одна из этих неизвестных масштабный коэффициент, а , который с помощью (7) и (8) связывают с дифракционной эффективностью П . Остальные неизвестные находятся в выражениях из раздела 2. Обе нелинейные системы алгебраических уравнений для когерентного случая (7) и некогерентного случая (12) будут решаться итеративным методом Ньютона.

4. Метод Ньютона

4.1.Описание метода Ньютона

МН заключается в замене системы нелинейных алгебраических уравнений на эквивалентную линейную систему. Пусть имеется нелинейная система:

буемое распределение амплитуды порядков, получаем:

q ( n ) а = ( - 1) ^N sin c ( n ) -

N ,                   ,                     (19)

- 2 Z ( - 1) k 2 z k sin c (2 z k n )

k = 1

n = [0, N ].

Система нелинейных уравнений (18) для когерентного случая примет вид fn(z) = - q(n) z о + (-1) N sin c(n)-

N                               ,            (20)

-    2 Z(-1) k 2 zksin c(2 zkn)

k = 1

n = [0, N ], где z0 = а - масштабный коэффициент.

Применим метод Ньютона:

• -    q ( n ) z 0 + ( - 1) ^N sin c ( n ) -

• N

• -    2 Z ( - 1) k 2 z k sin c (2 z k n ) - q ( n )( z 0 ^{+ 1} - z 0 ) - (21) k = 1

Nk

-    4 Z(-1) cos(2nzkп)(zk+1 - zk)=0

k = 1

Линейную систему (21 ) можно представить в виде:

a nk z k ^{+ 1} = b^l n , n = [0, N ], k = [0, N ],            (22)

где an о = q(n)> Kk =4(-1) k cos(2 nzkп), bln = (-1) N sin c(n) +

N

+ 4 Z ( - 1) k z k (cos(2 nz k п ) - sin c (2 nz k ))

k = 1

f n ( z ) = 0, n = [0, N ],                           (17)

где z = ( z ₀ , z 1 ,..., z_N ) . По МН (17) можно заменить на линейную систему:

fn (zi) + Z f(zi) (zj+1 - zj) = 0 , (18) j=0 dzj n = [0, N ], где индексы i и i+1 показывают принадлежность приближенного решения разным итерациям.

Для решения системы (17) задают начальное приближение z ⁰ и решают систему (18) до требуемой точности решения. На каждой итерации производиться пересчет коэффициентов линейной системы.

4.2.Описание четной решетки

Зададим точечное распределение амплитуды порядков q(n) с фазой 0 или п . Используя выражения (6) и (7), связывающие решеточный отклик и тре-

5. Градиентный метод

С помощью ГМ методом можно использовать дополнительные степени свободы для увеличения дифракционной эффективности решеток. ГМ «следит», чтобы за областью задания порядков не было дополнительных «паразитных» порядков дифракции. При этом число нулей решетки остаётся таким же. Выберем функционал в виде:

ML.

E = X9 e (n ) - p0(n ) ) ,                    (23)

n = 0

где p ₀( n ) = p * q ( n ) для n = [0, N ] и p ₀( n ) = 0 для

_      1

остальных n, здесь p =-------.

2* N + 1

Шаг итерации выберем в виде:

ti

E

N

Z k = 1

dE ^{d z} k

Тогда итерационный процесс можно записать :

i + 1

zk

z _k ⁱ

^- t i

дЕ ^{d z} k

k = [1, N ],

где dE  M

• -7— = Z ¹⁶ P e ( p ²^ ⁿ ) ^- p 2 ⁽ⁿ ) ^)x

• 6.    Численные результаты

  • 6.1. Метод Ньютона

^z k   n = 0

x (-1) ^{k + 1} cos( 2 nz k п )

Для решения линейной системы уравнений применялся метод Гаусса, а так же его модификация. Распределение нулей в начальном приближении выбрано равномерным. После каждой итерации проверяется физичность нулей: принадлежность отрезку [-0.5, 0.5] и очередность следования. Если это не выполняется производиться корректировка. Итерационный процесс сходится, как только корректировка подберёт приемлемые нули.

Использование МН позволяет получить точное решение задачи, но при низкой дифракционной эффективности для заданного распределения порядков. При этом все порядки имеют заданную фазу 0 или п . Дифракционная эффективность представлена в первом столбце таблицы.

Как видно она убывает с возрастанием числа генерируемых порядков. В тоже время возрастает линейно число итераций, необходимых для получения точного решения (с нулевой ошибкой). Были получены точные решения для числа порядков до 25. Начальное приближение выбиралось случайным.

Было исследовано как изменяется дифракционная эффективность при обнулении части паразитных порядков (эти нулевые порядки включались в систему уравнений). Число нулей решетки при этом возрастает, эффективность падает, а возникают новые паразитные порядки в области более высоких частот.

На рис. 3-5 приведен пример расчёта решетки МН. Решетка имеет 8 нулей (то есть восемь скачков фазы на л ) и генерирует 9 равных по интенсивности порядков. Остальные порядки являются паразитными. Нули решетки симметричны. Для сравнения эта же решетка рассчитывалась другими методами.

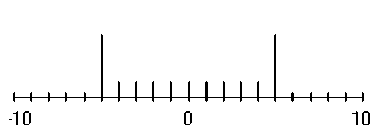
Рис.3 Полученное распределение интенсивности порядков в Фурье-плоскости. для МН

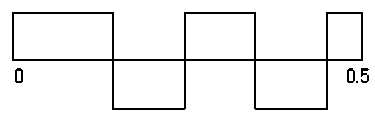
Рис.4 Половина полученной решеточной функции П =30,93%

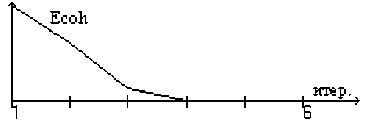
Рис.5 Ошибка решения от числа итераций.

• 6.2. Метод Дамманна.

В МД происходит перебор фаз (0 или л ) всех порядков с целью нахождения максимальной эффективности. Результаты приведены в третьем и четвёртом столбце таблицы. Как видно эффективность повысилась, но на это затрачивается большое количество итераций И * 2 N ^{- 1} . При этом не для всех распределений фаз существовали точные решения данной задачи. На рис. 6-8 приведен пример расчёта решетки методом Дамманна.

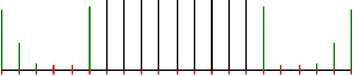
•10                  0                    10

Рис.6 Полученное распределение интенсивностей порядков в Фурье-плоскости для МД

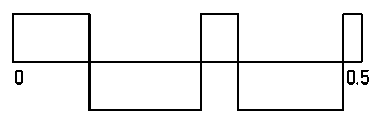
Рис.7 Половина полученной решеточной функции П =51,73%

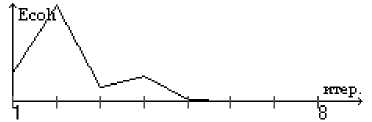
Рис.8 Ошибка решения на каждой итерации.

• 6.3. Градиентный метод наискорейшего спуска

• 6.4.    Гибридный итерационный метод

В случае ГМ начальное приближение и корректировка не менялась. После запуска итерационного процесса идёт поиск минимума функционала (23). На достижение точного решения необходимо затратить большое количество итераций. Функция цели имеет множество минимумов. В какой из них попадёт метод, зависит от начального приближения. На каждой итерации происходит подбор шага в сторону минимизации функции цели. Сначала пробуется шаг из ур.(24). Если он не подходит, берётся шаг в два раза меньше теоретического и так далее. Уменьшение шага ограничено. Градиентный метод позволяет получить решение с высокой эффективностью, но с большой ошибкой (30%-50%). Результаты работы ГМ даны в пятом столбце таблицы.

Была исследована возможность использовать совместно МН и ГМ. То есть по полученным нулям одного метода запускали итерационный процесс другого метода. Есть два варианта последовательного использования алгоритмов МН+ГМ или наоборот ГМ+МН. В первом варианте методы не стыкуются. МН находит точное решение для определенных фаз источников, а ГМ подбирает их сам. Поэтому при переходе от МН к ГМ последний “ломает” полученное распределение интенсивностей, изменяя нули решетки. Второй вариант дал интересные результаты. ГМ находит решение с хорошей эффективностью, но с большой ошибкой. Результаты работы ГМ в пятом столбце таблицы. Далее полученное распределение фаз порядков и нули решетки служат начальным приближением для МН. Он уменьшает ошибку до нуля, в тоже время оставляя эффективность на том же уровне. Количество итераций в ГИМ равно сумме седьмого и последнего столбцов таблицы. Эффективность приведена в предпоследнем столбце таблицы.

На рис.9-11 приведен пример промежуточного расчёта решетки градиентным методом.

На рис. 12-14 приведен пример окончательного расчёта решетки ГИМ=ГМ+МН.

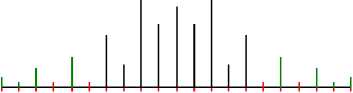
-10                   0                    10

Рис.9 Полученное распределение порядков в Фурье-плоскости для ГМ

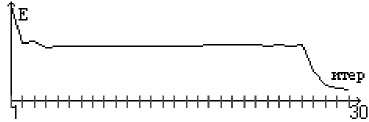
Рис.11 Ошибка решения на каждой итерации δ =49,86%

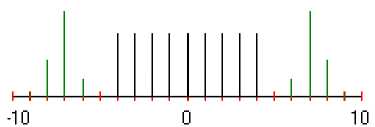
Рис.12 Полученное распределение источников для ГИМ

Рис .13 Половина полученной решеточной функции η =66,32%.

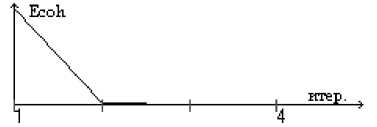
Рис.14 Ошибка решения на каждой итерации.

J                                              0.5

Рис.10 Половина полученной решеточной функции η =69,37%.

Таблица. Численные результаты расчета решеток разными методами.

M	η н ,%	И н	η Ђ ,%	η д ,%	δ д ,%	Ид	η д н ,%	Идн
3	66,42	4	66,42	65,27	13,77	2	66,42	+4
5	48,22	5	77,39	76,25	10,64	30	77,39	+3
7	37,71	5	65,52	72,21	45,81	18	65,52	+6
9	30,93	6	51,73	69,37	49,86	30	66,32	+4
11	26,21	8	60,59	63,39	31,19	30	59,42	+5
13	22,73	18	46,70	60,64	63,50	34	70,01	+6
15	20,07	15	54,54	65,47	13,87	36	62,16	+3
17	17,96	17	47,43	70,02	117,0	7	50,50	+6
19	16,26	9	40,35	63,23	57,83	6	56,41	+5
21	14,85	9	48,09	61,00	18,19	77	60,30	+4

ηн,% , ηЂ,% ,ηд,% , ηдн,% - дифракционная эффективность методов Ньютона , Дамманна (на основе Ньютона), градиентного и гибридного ( градиентный потом Ньютона) соответственно; Ин , И , Идн- число итераций для методов Ньютона, градиентного и гибридного; число итераций ме- тода Дамманна можно вычислить приближенно по формуле Ин * 2N-1 ;

δ д ,% - ошибка полученного промежуточного распределения интенсивности градиентным методом, для остальных методов ошибка составляет меньше 10 ^{- 6} , что можно принять за точное решение.

7.Заключение                        6.

Из всех методов только смешанный позволяет получить решетку с высокой эффективностью, точным решением и затратив на нахождение малое ко-       ^7.

личество итераций. Что позволяет, надеется на его применение в других расчётных задачах.

Работ частично финансировалась Российским фондом фундаментальных исследований (гранты 9. 98-01-00894, 99-01-39012).