Расчет дифракционных оптических элементов для разделения фокусировки излучения различных длин волн

Расчету дифракционных оптических элементов (ДОЭ) для преобразования волновых фронтов и фокусировки когерентного излучения в заданную область посвящено большое количество работ [1-3]. Как правило, расчет микрорельефа ДОЭ производится для одной определенной длины волны. Для работы с различными спектральными компонентами известны цветоделительные фазовые дифракционные решетки (color separation gratings), позволяющие разделить три различные спектральные компоненты освещающего пучка по -1, 0 и 1

дифракционным порядкам [4-6].

В данной статье предлагается метод расчета * спектральных’ фазовых ДОЭ. обобщающих цветоделительные решетки. Предлагаемые ДОЭ позволяют: 1) сфокусировать три различных спектральных компоненты освещающего пучка в три одинаковые фокальные области, 2) при изменении длины волны изменять конфигурацию области фокусировки для трех различных длин волн.

2. Цветоделительные решетки

Для описания работы ‘спектральных’ ДОЭ предварительно рассмотрим принцип работы цветоделительных фазовых дифракционных решеток.

Решетка, позволяющая разделить три спектральные компоненты, соответствующие длинам волн

ветствуют N-ступенчатой аппроксимации линейных фазовых функций, обеспечивающих фокусировку в порядках -1 и +1 соответственно. Доля энергии данных спектральных компонент, фокусируемая в порядках 1 и -1, соответствует эффективности N-уровневой линейной решетки;

E(N) = 8тсЧл / N\ (5)

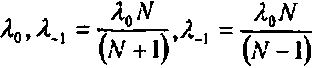
по 0, +1 и -1 дифракционным порядкам имеет на периоде N ступенек равной ширины [3-6]. Высота ступенек определяется по формуле

**^#*Ю     ®

где По- показатель преломления материала решетки для длины волны Хо.

Пренебрегая дисперсией материала решетки [4-6] получим, что решетка (2) для плоских пучков с длинами волн (1) формирует следующие фазовые набеги.

ф₀ = 2л^- • i,

Ф_х = 2л • i = 2л • i - ~ ' ' ,(3)

Ф_ч = 2л • ! -— = 2л • i +-----

A.N

С учетом 2л-периодичности фазы, представим распределения фазы (3) в виде:

,               2;Т - /

Фй = 0,^ --—,

Согласно (4), для длины волны Хо фазовый набег равен нулю и. следовательно, данная спектральная компонента дифрагирует в нулевой порядок. Для длин волн Х+1 и X.; фазовые набеги (4) соот-

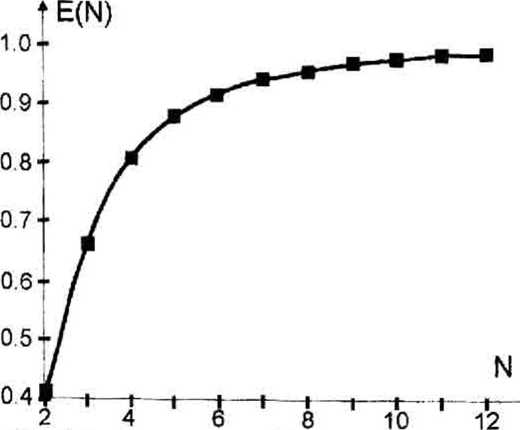
Рис. I. Энергетическая эффективность линейной рететки, квантованной по Nуровням

График функции E(N) приведен на рис.1. Например, при N=4 решетка (2) направляет 100% энергии спектральной компоненты Хц в ну левой порядок и 81% энергии спектральных компонент Хи=0.8Хо и Х.1 =1.33% в порядки +1 и -1.

• 3.    Спектральные ДОЭ для фокусировки в набор одинаковых фокальных областей

Использование комбинации цветоделительная решетка - линза позволяет сфокусировать три спектральных компоненты в три точки в фокальной плоскости линзы. Рассмотрим расчет спектрального ДОЭ - фазового ДОЭ, выполняющего разделение и фокусировку трех спектральных компонент (1) в три одинаковых фокальных области заданной формы, расположенных в одной или различных плоскостях вдоль оптической оси (рис.2). Микрорельеф спектрального ДОЭ предлагается определить в виде:

^(“) = Т—р—л ф(«; Л) = 2л • (н₀ - 1)

-А-^Ни)^^))]

некогерентных между собой плоских пучков с длинами волн (1). Для описания связи распределения интенсивности поля с фазовым набегом Ф(и; Я) будем использовать интеграл Кирхгофа в приближении Френеля:

7(х; z, Я) =

где ф(и) е (0,2л) - фазовая функция, рассчитанная из условия фокусировки плоского монохроматического пучка с длиной волны Хо в область D в плоскости z=f. Дтя удобства дальнейших выкладок выделим из функции 9?(и) фазовую функцию линзы в явном виде

Т" f exp U ^ Ф(«; А») ^х

AZ ^J         Я

х ехр — (х - u) \d и

^(u) = mod2;r

м

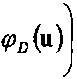
При ^^ фазовый набег, вносимый спектральным ДОЭ, соответствует фазовой функции ф(и), что обеспечивает фокусировку в область D в плоскости z=f.

Для пучков с длинами волн Л+] и X., фазовые набеги, с учетом 2л-периодичности фазы, описываются функциями;

где добавка к линзе pn(u) обеспечивает фокусировку сходящегося сферического пучка с фокусом f в область D пои z=f.

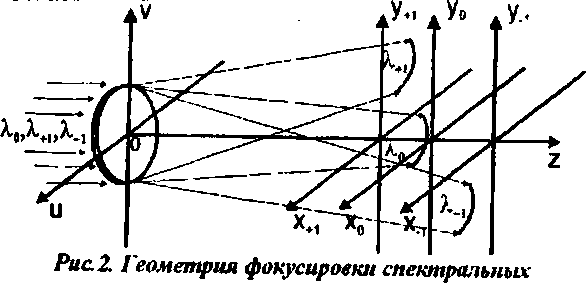
компонент^) в набор областей

у 4. 1

Ф(и; Л^ = — ■-. - (р'ц) + О(^(и))) -

А’ + I                   х

--— ^(и) + ТзД^и)),

Ф(и; Я.,) = — ^   (^(и) + G(p(u))) =

N - 1              X

- --~■ ^(и) - 7v(p(u))

Функция

Функция G в (6) описывает нелинейное преобразование фазы

^Fn^) = — int 7-j

N I 2л )

^(u) = mod2J- р(и) + $%г(и) + ^(и)

по закону фазового набега цветоделительной решетки для длины волны Хо;

G^ = 2л • int

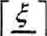
_N.

,^ е [0,2л)

Функции фДи) = -^хои,^и):=--^—и2      (10)

в (8) соответствуют фазовым функциям линзы и призмы и предназначены для разделения областей фокусировки для различных спектральных компонент.

Отметим, что функция Ф(и; Яо) в (6) соответствует фазовому набегу, формируемому спектральным ДОЭ для длины волны ^- При этом для пучка с длиной волны Я * Яо, фазовый набег имеет вид:

ф(ц;Я) = ^ф(и;Я₀)                (11)

Проведем анализ работы спектрального ДОЭ (6)-(10) для освещающего пучка, состоящего из трех

в (13) описывает квантование фазы по N уровням. Нелинейная операция квантования Т^^и)) в (13) приводит к появлению дополнительных дифракционных порядков [7-8]. Проанализируем работу спектрального ДОЭ при длине волны Хц. /Для этого разложим комплексную амплитуду поля w(u; Яи) = ехр(/Ф(и; Я+1)) непосредственно за плоскостью ДОЭ в ряд по дифракционным порядкам [7-11|:

ехр(/ф(и; Я.,))

Ес« ехр^

X + 1 / х

—д— Ru) +

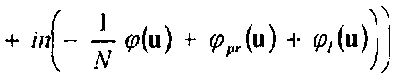
где

с»

/ |Мл-И Д’о ( ЛИ \ ^f - Л (- 1) Smc' — । ехр 1 —— I, \ А > ч А )

/? = ! + рХ,р = 0,±1,±2, . . . -

0,л у 1 + рХ

коэффициенты Фурье в разложении функции ехрО^Й))-

Согласно (15), в первом порядке дифракции (при п=1 в (15)) формируется пучок с фазовой функцией

Фи(«/Л|) = ^(“) + ^(«) + ^/(и). (17)

Для оценки структуры поля, формируемого пучком с фазовым фронтом Ф+1(и; Хи), подставим фазовую функцию (17) в интеграл Кирхгофа-Френеля (12) Проводя несложные преобразования, представим распределение интенсивности, формируемое в первом дифракционном порядке при z = z+l

в виде:

N

(i*)

2,,z

J exp U

D^

- ^(u)) x

x exp

u

где

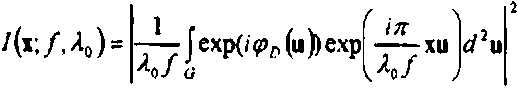
-(20)

- распределение интенсивности при z=f, формируемое при фазовом фронте ^D(u) для пучка с длиной волны Хо. По определению функции ^л(ц), распределение интенсивности (20) соответствует фокусировке в область D. Согласно (19), (20) распределение интенсивности, формируемое спектральным ДОЗ в первом порядке при длине волны Х41, соответствует фокусировке в смещенную на вектор к, область D в плоскости z = z.,. Масштабный множитель

Л, = t + 4 (21)

в (19) описывает изменение физического размера области D. вызванное уменьшением размера дифракционного пятна

Akt^J = Дк,, 2.,)//^ = — к/ / а), (22) Л:

где о - характерный размер апертуры ДОЗ.

Доля энергии Е спектральной компоненты Х.|, фокусируемая в порядке ^1 соответствует квадрат) модуля коэффициента Фурье С| (см.(5)) и при N>3 составляет более 80%

Повторяя приведенные рассуждения для пучка с длиной волны)-! получим. ‘ПО фазовый фронт, формируемый ДОЗ (6НЮ) в основном -1 порядке дифракции соответствует фокусировке при

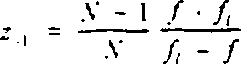
в смещенную на вектор -Хо область D. При этом изменение физического размера области D описывается множителем

Р-, = 1 - X <24>

Jl

Параметр J, в (10), (18), (23) позволяет варьировать положением плоскостей фокусировки. В частности, полагая f_t = NJ в (18), (23), получим что z^ = z₄ = J . В этом случае спектральный ДОЗ фокусирует спектральные компоненты (1) в три, разнесенные на вектор Хо области D в одной плоскости при z=f.

В заключение отметим, что для уменьшения частоты микрорельефа целесообразно рассчитывать спектральный ДОЗ как дополнение к тонкой линзе с фокусом f В этом случае вместо функции ^(и) в (б) следует использовать функцию ^ (и), рассчитанную на фокусировку сходящегося сферического пучка с фокусом f в область D при z=f,

• 4.    Спектральные ДОЭ для фокусировки в различные фокальные области

Рассмотренный в пункте 3 метод расчета позволяет разделить и сфокусировать спектральные компоненты (1) в три области одинаковой формы в одной заданной плоскости или в трех различных плоскостях вдоль оптической оси. Рассмотрим расчет спектральных ДОЭ, позволяющих при изменении длины волны по закону’ (1), изменять конфигурацию фокальной области.

Длины волн в (1) и фазовые набеги (4) для цветоделительной решетки (2) не являются независимыми между собой. Поэтому в общем случае метод расчета (6)-(10) может быть модифицирован на случай фокусировки двух различных длин волн из (1) в две различные области D_o и Д. Обозначим ^(u),^(u) - фазовые функции для фокусировки пучков с длинами волн Хо, Х₄[ в области Do и D]. Переопределим функцию ^(и) в общем выражении для структуры микрорельефа спектрального ДОЭ (6) в виде:

^(u) - ^od2„|^- —^ 1 ^(и) + P](u)j (25)

При ^(и) (25), спектральный ДОЭ для пучков с длинами волн X» и Х4 формирует в 0 и +1 порядках дифракции пучки с фазовыми функциями

Ф0(и; Л) = *),                    (26)

ф4|(ч;^-1) = ^(и),                     (27)

что обеспечивает фокусировку в области Do и D], соответственно.

При использовании длины волны X.] ДОЭ (6), (17), (8) формирует в основном -1 порядке пучок с фазовой функцией

Фч(и; 2.J = 2p(u) - ^(u) (28)

В случае произвольных фазовых функций ^(и) и ^ (и) структура области, формируемой при А=А,|. не определена. Ряд результатов удается получить при использовании в качестве функций р(и), Ф1(^и) фазовых функций фокусаторов - ДОЭ, рассчитанных в приближении геометрической (лучевой) оптики (3]. Предположим для простоты, что спектральный ДОЭ рассчитывается как добавка к тонкой линзе с фокусом f. В этом случае функции Ф₀(и),ф,(и) соответствуют фазовым функциям для фокусировки сходящихся сферических пучков с длинами волн Х_о, Х-н в области D) и Dj при z=f. Фокусаторы обладают интересным свойством; при умножении фазы фокусатора, рассчитанного на фокусировку сходящегося сферического пучка, на константу р, происходит р-кратнос масштабирование области фокусировки [3].

Рассмотрим два примера выбора функции ^(п), <р_х (и), позволяющих работать с тремя длинами волн Хо, Х₊₁, X.).

Пример 1.

Пусть ф(и)- фазовая функция фокусатора, а ^(и) - фазовая функция N-порядковой дифракционной решетки. Тогда при X=X._t фазовая функция 2р(и) в (28), реализует фокусировку в область 2xD, а функция ^(и) - мультипликацию области 2xD по N порядкам. В этом случае элемент, соответствующий суперпозиции ‘спектральный ДОЭ - тонкая линза¹, при Х=Хо реализует фокусировку в область D, при Х=Х₊₁ - в набор из N точек, а при X=X.i - в набор из N областей с размером 2D.

Пример 2.

Пусть ^(и), ф_х (и) - фазовые функций фокусаторов пучков прямоугольного сечения в отрезки |д^ <  d, у = 0 и |у| < d_x, х - 0 . Тогда при Х=Х] распределение фазовая функция (28) соответствует фокусировке в прямоугольник с размерами (4d)x(2di) [9]. При указанном выборе функций р(и), ^(и) спектральный ДОЭ при Х=Хо реализует фокусировку в отрезок оси Ох, при X=X^i - в отрезок оси Оу, а при X=X-i - в прямоугольник.

• 5.    Аспекты расчета квантованных спектрал ьн ых ДОЭ

Технология фотолитографии, традиционно используемая для изготовления ДОЭ, предусматривает квантование дифракционного микрорельефа по М уровням. Микрорельеф спектрального ДОЭ (6) содержит компоненту', соответствующую функции ^(и) и N-уровневую ступенчатую функцию G(p(u)). При квантованной по L уровням функции ^(и) микрорельеф (6) становится квантованным по M=NxL уровням.

Операция квантования приводит к снижению эффективности фокусировки и появлению дополнительных дифракционных порядков, снижающих качество формируемых изображений. Для компенсации погрешностей квантования на этапе расчета спектрального ДОЭ, функцию (р(и) в (6) для фокусировки пучка с длиной волны Хи целесообразно рассчитывать на основе итерационных алгоритмов расчета квантованных фазовых функций [10-12]. Алгоритмы ] 10-12] основаны на оптимизации непрерывной функции, являющейся отрезком ряда разложения по дифракционным порядкам квантованной функции комплексного пропускания.

Спектральный ДОЭ для пучков с длинами волн Л_±, (]юрмирует требуемые изображения только в основных + 1 и -1 дифракционных порядках. Изображения в паразитных’ порядках при п * ±1 в общем случае портят требуемые изображения Спектральные ДОЭ (6), (25). предназначенные для фокусировки двух длин волн Хо, Х.1 в две различные области D₍₎ и D], будем называть двухволновыми ДОЭ. Для двухволновых ДОЭ расчет функции ^(и) в (25) можно также провести с учетом влияния паразитных дифракционных порядков. Действительно, при Х=Х-| ДОЭ (б), (25) формирует в порядках дифракции пучки с фазовыми функциями

Ф„(и; Я.,) = ^-- Н«) +

• Г Л' + 1 , X ,

f --— Ни) + ^ (и)(29) и = (1 + pN),p = 0,±1,±2, . .

При п=1 (р=0) в (29) Ф„(и; 2^) = ^(и), что обеспечивает в основном первом дифракционном порядке фокусировку в область D). Пусть функция Ни) является квантованной по (N+1) уровням. При этом распределения фазы (29) принимают вид

Фя(и; Л,) = «^(и)^ = (1 + рХ\ р = 0,±1,±2, ...

Согласно (30). фазовый набег Ф(и; 2.J нс зависит от фазы Ни)и соответствует квантованной по N уровням функции ^Ди);

Ф(и;Л.,) = Fv(W(u))                  (31)

Таким образом, при квантовании фазы Ни) по N+1 уровням расчет двухволнового ДОЭ сводится к двум независимым задачам расчета квантованных фазовых функций/^..ДНи)) и ГД<р. (и)) из условия фокусировки пучков с длинами волн /^ X-i в области De и D; соответственно. При этом число уровней квантования рельефа двухволнового ДОЭ равно М = V - (.V -^ 1) Интересно отмстить, что рельеф дву хво.лнового ДОЭ (6), (25) можно определить непосредственно через дискретные значения fO = — у - 0,N,

о,0) = ^w = 0,^-1, принимаемые квантованными функциями /7+,(р(и)), ^feW)- Действительно, подставляя в (25) и (6) вместо функций

ф(1, j) = mod₂„

G(i, у) = 2д • modjV(y - /)

Выражения (32), (33) позволяют представить высоту рельефа двухволнового ДОЭ в каждой точке и апертуры через индексы (ij), соответствующие значениям квантованных функций ^^(^(и)), Fw(^(u)), в виде:

^=1^Г

2л-          _           , /. л х ------z + 2д • modv(y - I) N + 1

i = 0, N,j = 0, N - 1

Число уровней М = /V • (А' + 1) микрорельефа (34) можно уменьшить. Пусть d_b d₂ наибольшие делители чисел N, N+1; такие что N=p]db pi>l, N+l=p2d2, Р2>1. В этом случае, из квантованных функций F (^(и)) и /^ (^(и)), рассчитанных из условия фокусировки пучков с длинами волн Хо, Х^ в области D_fJ и D_b можно построить двухволновый ДОЭ с числом уровней рельефа М = р_хр_г по правилу:

^—j + lTrmod^dJ-d^

Pi                                                 (36)

/=от/>2 -1,; = о,л -i

Функция Ф(/, j; Я₊₁) с учетом 2л-периодич-ности имеет вид

ФО,/;^) = — ЛУ = 0,^-1     (37)

Р\ и соответствует отсчетам фазы F (^(u)), что обеспечивает фокусировку пучка с длиной волны Хц в область Dj.

Отметим, что поскольку одно из чисел N, N+l является четным, то число уровней рельефа двухволнового ДОЭ всегда может быть уменьшено, по крайней мере, до N(N-H)/2 значений.

Расчет квантованных двухволновых ДОЭ для фо-кусировки в области Do и D] можно провести не только для длин волн Хо, Хд из (I), а также для двух длин Хо, Х;, связанных существенно более общим соотношением где М и N - взаимнопростые числа.

Формула (34) подсказывает строить двухволновый ДОЭ из квантованных по М и N уровням функций FM(p(u)) и ^(^(и)). Определим рельеф двухволнового ДОЭ через значения квантованных функций ^(^(и)) и /^(^(и)) в виде:

^Н^' ^;^ ⁼ ТТ^ —["ТУ' ^{+ 2?г} • ^Mo^ у Я 2д(и₀ - 1) VM                  J (39)

i = 0, М - 1, j = 0, N - 1

где M^ij) - некоторая неизвестная функция, принимающая целочисленные положительные значения. ДОЭ (39) при Х=Хо формирует фазовый набег х — z + 2л • mod^^y - d^ _Рг i = °, Р: " U = °* Pi ~ 1

ДОЭ (35) при Х=Х₀ формирует фазовый набег, соответствующий отсчетам фазовой функции F^ (^(u)). что обеспечивает фокусировку в область D.

При Х=Хд фазовый набег, формируемый ДОЭ (35). имеет вид

д.,)=

= 2,т

~~ -1-+ mod N\dj-d^ =

Ф{/, j; ^-) = ™ + 2лА/0(/, ») м i = 0, А/ - 1, у = 0, Л’ - 1

соответствующий с учетом 2я-периодичности фазы отсчегам фазовой функции ^(^(ц)). Это обеспечивает при Х=Хо фокусировку в область D. При Х=Х] фазовый набег, формируемый ДОЭ (39), имеет вид

Ф(/,У;А,)= a^r^F-L + M₀(_f, у) i = О, М - \,j = О, N - 1.

Для фокусировки пучка с длиной волны X] в область Di, функция M₀(ij) в (39) долна выбираться из условия равенства по модулю 2л выражения (41)

отсчетам квантованной функции ^лМ))- В результате для расчета функции M^iJ) получим уравнение

. М \ i

1л— —

N [м

+ M_Q(ir У)

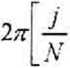
+ Л/,О, у)

Решетка (47) может быть использована при аналитическом расчете спектральных фокусаторов пучков с длинами волн (38) в области D_o и Di. В этом случае достаточно общем выражении (6) переопределить функции G^ и ^(и) в виде:

/ = О, М - V = О, .V - L

б(^) = 1л- mod,_v

(42) где M^iJ) - произвольная функция, принимающая целочисленные значения.

Непосредственной подстановкой можно убедиться, что решение уравнения (42) имеет вид:

pWoO' У) = ±ai0' ~ 0 + Nz

1^1 ( у) = ±«₂0‘ - О + Mz (43)

/ = О, Л/ - 1,у = О, N - 1.

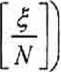
,£е[о,2яг) (48)

где «], «2 - целые числа, определяемые из решения уравнения

М • а, - N • а_г = ±1,

az- наименьшее целое число, выбираемое из условия неотрицательности функции Motij). Отметим, что поскольку числа М и N предполагаются взаимнопростыми, то уравнение (44) всегда имеет решение в целых числах по теореме о наибольшем общем делителе.

Согласно определению z, уравнение (43) может быть записано в виде:

Г ^МЛ1. У) = mod _v(± ОТ) (у - /))

Ь^О, у) = modM(± а2(/ - 0)       (45)

/ = о, м - \,j = о, .v - 1.

При этом формула для микрорельефа двухволнового ДОЗ принимает вид:

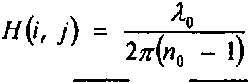
2л-

— \ * 1л • modv(± ax^j о, л;у = о, ^ - 1

Сравнение уравнений (35) и (46) показывает, что использование более общего соотношения (38) для длин Хо, X] не приводит к увеличению высоты микрорельефа ДОЗ (46) по сравнению с ранее рассчитанным ДОЗ (35). Следует также отмстить, что при Л^р;di, pi>l, Л/=р2б₂, р2>1 число уровней L-NM микрорельефа (46) можно уменьшить до рр; значений.

Из формулы (46) несложно получить уравнение для цветоделительной решетки для разделения спектральных компонент (38) по 0 и +1 порядкам. Такая решетка имеет на периоде N ступенек равной ширины с высотой dt = , ^ , modA.(a,/), i = 0, N - 1 (47)

Яи) = mod₂J- ^Н«) + ^(u)j       (49)

V Л             )

Несложно видеть, что спектральный ДОЗ (6), (48), (49) для пучков с длинами волн (38) в 0 и +1 порядках дифракции формирует пучки с фазовыми функциями ^(u), ^(u), *fro обеспечивает фокусировку в области Dn и D] соответственно.

6. Результаты расчетов

Для оценки работоспособности предложенного метода приведем ряд примеров расчета спектральных ДОЗ.

Пример 1. Был рассчитан ДОЗ (6)-(10) как дополнение к тонкой линзе с фокусом f для разделения и фокусировки спектральных компонент (1) в три отрезка длины в плоскости z=f. В качестве функции р(и) в (6)-(10) использовалась фазовая функция фокусатора сходящегося сферического пучка с фокусом f в отрезок

«рии = mod. ------ 7?--- (50)

V 2I 2     12

где R - радиус апертуры ДОЗ, d - длина отрезка фокусировки.

Расчет спектрального ДОЗ (6)-(10), (50) проводился для следующих параметров; длины волн Х()=0.525мкм, Х^1=0.393мкм, 7^! 1=0.656м км (N=4 в (1)), длина отрезков фокусировки d=30A(X), (A(X)=Xf/R), радиус апертуры ДОЗ К=2.5мм, фокус линзы б=500мм, параметры призмы и линзы в (10) хо=(0,10А(Хо)), f,=Nf=2000 мм.

Полутоновое изображение рассчитанного рельефа спектрального ДОЗ приведено на рис. За. Распределение интенсивности, формируемое спектральным ДОЗ (6)-(10), (50) для освещающего пучка, состоящего из трех некогерентных между собой плоских пучков с указанными выше длинами волн, приведено на рис.Зб. Рисунок 36 показывает высокое качество фокусировки в три отрезка. Различные длины и интенсивности отрезков на рис.Зб объясняются различным размером дифракционного пятна Д(Х) дтя различных длин волн. Левый, центральный и правый отрезок на рис.Зб соответствует компонентам X 1 =0.656, Хо=О.525мкм и Х„;=0.393мкм, соответственно.

где aj определяется из решения уравнения (44).

За)

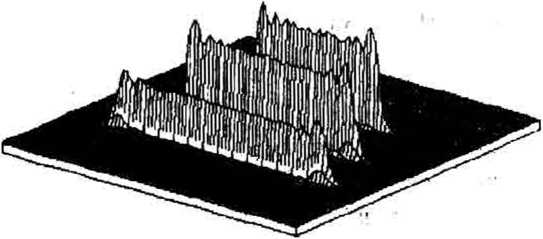
Рис 3. (а) Полутоновой рельеф спектрального ДОЭ для разделения и фокусировки спектральных компонент Xq=0.525mkm, Х_л1=0.393мкм, Л_,=0.656.мкм в три отрезка;

(б) Распределение интенсивности в плоскости фокусировки

Пример 2. Был рассчитан спектральный ДОЭ (6), (25), позволяющий при изменении длины волны по закону (1), изменять конфигурацию фокальной области. ДОЭ (6), (25) был рассчитан как дополнение к линзе для фокусировки компоненты Х_о=О.525мкм в отрезок длины 2ОД(Хо), компоненты Х,,=0.393мкм - в четыре точки и компоненты Х-1=0.656мкм - в четыре отрезка с длиной 40Д(Х.]). В качестве функции р(и)в (6), (25) использовалась фазовая функция (50) фокусатора в отрезок. Для компенсации влияния паразитных дифракционных порядков при фокусировке компонент Х+ь X.] в фазу (50) была дополнительна введена фазовая функция 2# X?

призмы <рДг)

yov при >'о=2Д(Хо). В качест-

ве функции ^(и) в (б), (25) использовалась фазовая функция четырех порядковой дифракционной решетки, имеющей на периоде р (р=0,3571мм) следующий вид.

0, п е [О, р/4)

^W-

л, п^р^р^ л/1 ,п е[ р/2,3 р/А^

Зл/4, ле[3 р/^, р}

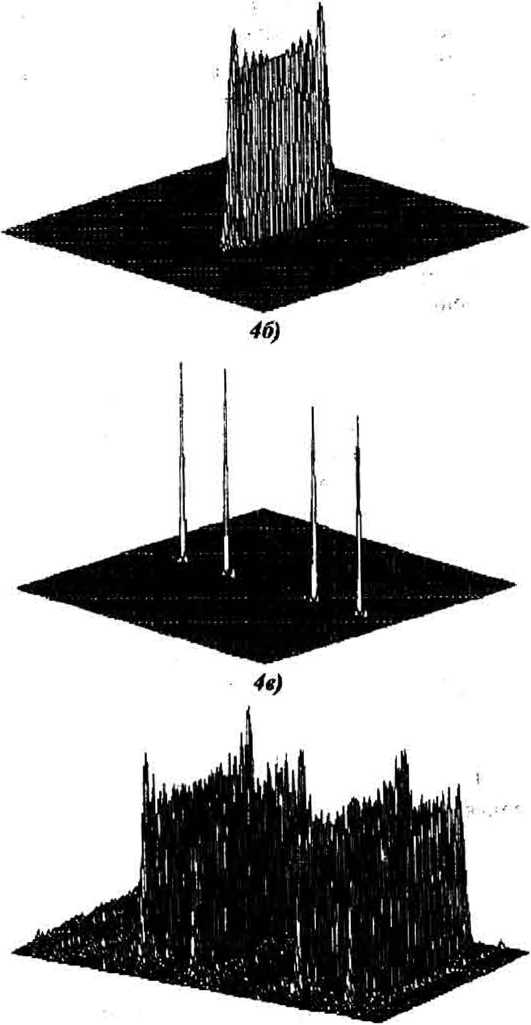
Четырехпорядковая решетка (51) фокусирует 81% энергии освещающего пучка в порядках -2, -1, +1. +2. Полутоновое изображение рассчитанного рельефа спектрального ДОЭ приведено на рис.4а). Распределения интенсивности, формируемое спектральным ДОЭ для плоских пучков с длинами волн Хо=О.525мкм, Хя=0393мкм и Х.1=О.656мкм приведены на рис.46), 4в), 4г) и ясно показывают структуру излучения, сфокусированного в отрезок, четыре точки и четыре отрезка.

4а)

4г)

Рис. 4. (а) Полутоновой рельеф спектрального ДОЭ для фокусировки спектральных компонент (1) в отрезок, четыре точки и четыре отрезка; (б,в,г) Распределения интенсивности в плоскости фокусировки для

Ао=О.525мкм (6), A._+j=0.393mkm (в), 1 j=0.656mkm (г)

Пример 3. Был рассчитан спектральный ДОЭ (6), (25) с квадратной апертурой 2,5x2,5мм для фокусировки компоненты Хо=О.525мкм в квадрат 20Д(Хо)х20Д(Хо) и компонент X+i=0.393mkm, X. ,-0.656mkm - в отрезки с длинами 40Д(^), 4ОД(Х.О осей Ох и Оу, соответственно. В качестве функций р(и) и ^(и) в (6), (25) использовались фазовые функции фокусаторов сходящегося сферического пучка с фокусом f в квадрат размером стороны КД(^)

ф(и) = mod2 f^^2 + v2) I           (52)

и в отрезок оси Ох длины 2КД(Х-0

, х 1лК

                    (53)

а где а - размер стороны апертуры ДОЭ.

ДОЗ (6), (25), (52), (53) при длине волны X.] формирует в основном -1 порядке пучок с фазовой функцией

Ф- ^u; Aj = 2ф(и) - ^(и) = ^- v² (54) а

Фаза (42) соответствует фазовой функции фо-кусатора сходящегося сферического пучка в отрезок оси Оу длины 2КД(Х.]).

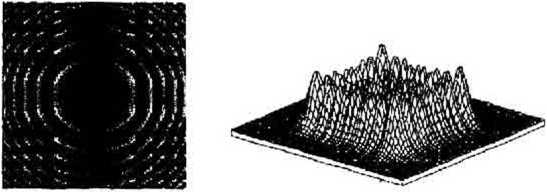
Полутоновое изображение рельефа спектрального ДОЗ (6), (25), (52), (53) приведено на рис.5а). Распределения интенсивности, формируемое спектральным ДОЭ для пучков с длинами волн Хо=О.525мкм, Х„1=0.393мкм и Х_]=0.656мкм приведены на рис.56), 5в), 5г) и ясно показывают структуру излучения, сфокусированного в квадрат и отрезки.

Sa)               56)

5в)                 5г)

Рис. 5. (а) Полутоновой рельеф спектрального ДОЭ для фокусировки спектральных компонент (1) в квадрат, отрезок оси Ох и отрезок оси Оу;

(б,в,г) Распределения интенсивности в плоскости фокусировки для 1(р=0.525мкм (6), Х,1=0.393мкм (в), А._₁=0.656мкм (г)

Пример 4. Были рассчитаны две квантованные спектральные дифракционные решетки для формирования четырех порядков -2, -1, +1. +2 при длине волны Х_о и трех порядков -1,0, +1при длинах волн X-i=3Xo/4 и X₊i=9Xq/4, соотвегственно Расчет квантованных спектральных решеток (период р) проводился по формулам (35) и (46) на основе квантованных фазовых функций четырехпорядковой решетки (51) и трехпорядковой решетки

,       (2л- / 3,и е [0,р / 2)

Ф'М = I О,, е b / 2,,)

Значения интенсивностей порядков, соответствующие квадратам модулей коэффициентов Фурье в разложении функции exp(/^(w)), для решетки (55) равны /.|=0.304. 70=0.25, L] =0,304. Следовательно решетка (55) концентрирует 85% энергии в порядках -I, 0, +1.

Рельеф квантованной спектральной решетки (35), (51), (55) для фокусировки компонент Xq, X+i=3X(/4 представлен на рис. 6а), а рельеф спектральной решетки (46), (51), (55) для фокусировки компонент Х_о, Х_]=9Хо/4 - на рис. 7. Интенсивности дифракционных порядков, формируемых решетками на рис. 6а) и рис.7 при освещении решеток плоскими пучками с длинами волн Хо, Х+|=ЗХ4 и Х_о, Х.]=9Хс/4 совпадают и показаны на рис.66) и 6в).

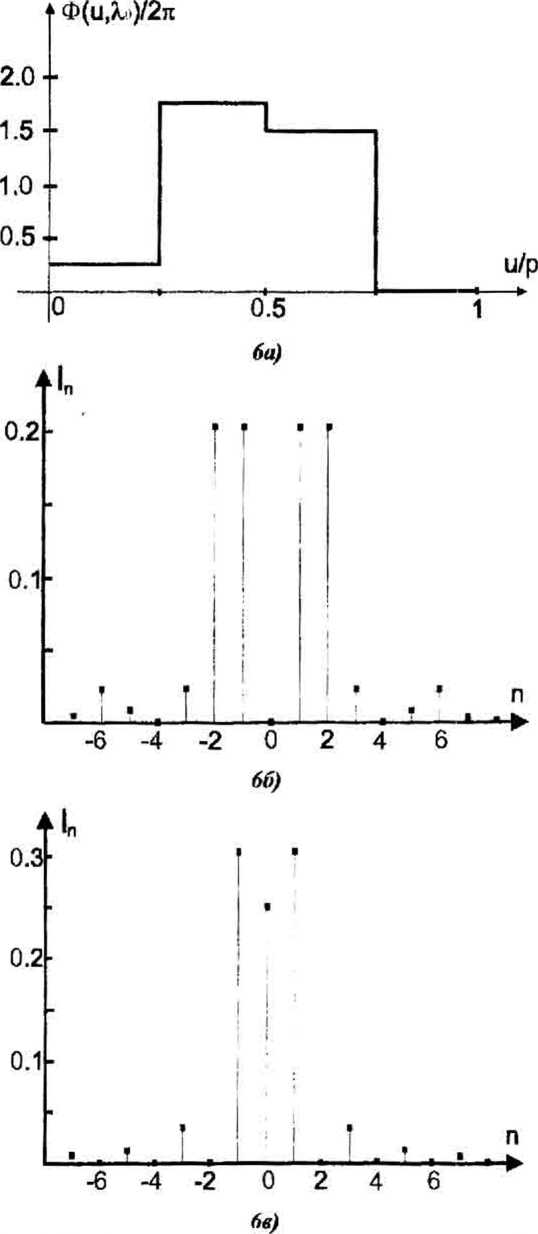
Рис. 6 (и) Фаза ни периоде спектральной решетки для формирования четырех порядков (-2,-1,* 1,*2) для компоненты Лои трех порядков (-1,0,* 1) для X^=3XV4; (б,в) Интенсивности дифракционных порядков решетки для Ао (6), Л+1 (в)

Рис. 7. Фаза на периоде спектральной решетки для формирования четырех порядков (-2,-1 Д1Л2) дчя компоненты Хо и трех порядков (-1,0^1) для X*t=9X(/4

Заключение

В данной работе разработан метод расчета спектральных ДОЭ для разделения и фокусировки различных спектральных компоненты в различные фокальные области. Проведен анализ эффектов квантования спектральных ДОЭ и разработана процедура расчета квантованных спектральных ДОЭ. Результаты проведенных численных расчетов (рис. 3-6) демонстрируют высокую работоспособность разработанного метода расчета спектральных ДОЭ.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 96-15-96026)