Расчет дифракционных структур для фокусировки поверхностных электромагнитных волн

Большое число публикаций, посвященных изучению поверхностных электромагнитных волн (ПЭВ), обусловлено перспективами их применения в нанолитографии, оптических сенсорах, волноводной оптике, микроскопии. Оптическая обработка информации в наномасштабе является одним из основных направлений, где использование ПЭВ является особенно перспективным [1–3].

Для преобразования и фокусировки ПЭВ используются дифракционные ми кро- и наноструктуры, расположенны е непосредственно на поверхности распространения ПЭВ [4–10]. Результаты работ [4– 8] указывают на сходство между распространением и дифракцией ПЭВ и распространением и дифракцией света в обычной диэлектрической среде. В частности, в [11] рассмотрен эксперимент по интерференции ПЭВ, являющийся аналогом знаменитого эксперимента Юнга по дифракции света на двух щелях. В [11] отмечено явное сходство между дифракционной картиной света на двух щелях и соответствующей интерференционной карт иной ПЭВ.

В скалярной теории дифракции широко используется представление дифрагированного поля в виде углового спектра плоских волн и дифракционного интеграла Кирхгофа [12, 13]. По аналогии со скалярной теорией указанные представления также используются для описания дифракции ПЭВ. Единственное отличие состоит в том, что в качестве длины волны излучения используется длина ПЭВ. В частности, в [11] записано интегральное представление электромагнитного поля на поверхности распро- странения через угловой спектр ПЭВ. В [10] указанное представление использовано для расчета линзы ПЭВ и моделирования распространения ПЭВ. В [7] для расчета линзы ПЭВ и описания дифракции ПЭВ использован интеграл Френеля-Кирхгофа.

Для расчета линз ПЭВ в [7, 10] используется подход скалярной теории, основанный на фазовой модуляции ПЭВ по закону тонкой линзы. В [10] для фазовой модуляции ПЭВ используется диэлектрическая структура переменной длины, расположенная на малом расстоянии над поверхностью распространения ПЭВ. Для описания прохождения ПЭВ через указанную структуру решается модельная задача дифракции ПЭВ на «плавающем» над поверхностью диэлектрическом блоке [10]. Модельная задача решается в рамках электромагнитной теории с использованием метода Ф урье-мод [14–16].

В данной работе использован аналогичный подход. Рассмотрено решение модельной задачи на диэлектрической ступеньке, расположенной непосредственно на поверхности распространения ПЭВ. Установлено, что фазовый набег, формируемы й при прохождении ПЭВ через ступеньку, хорошо описывается аналитической формулой, аналогичной формуле для набега фазы плоской волны при прохождении через однородный слой. Предложен новый тип амплитудно-фазовой модуляции ПЭВ, состоящий в изменении высоты ступеньки над поверхностью распространения ПЭВ, а не ее длины. Рассчитаны дифракционные линзы ПЭВ, использующие в качестве механизмов модуляции фазы изменения длины и высоты диэлектрической ступеньки.

Уравнение поверхностной электромагнитной волны и интегральные представления поля

В работах [10,11,7] авторы используют аналоги углового спектра плоских волн и интеграла Кирхгофа для описания распространения ПЭВ со ссылкой на классическую книгу Дж. Гудмена по скалярной теории дифракции [12]. Для корректности изложения приведем краткий вывод указанных интегральных представлений для ПЭВ непосредственно из уравнений Максвелла.

Рассмотрим уравнение ПЭВ на границе раздела металла и диэлектрика с диэлектрическими прони-цаемостями £ m , £ d . Пусть границей раздела является плоскость z = 0 , при этом среды £ m , £ d соответствуют областям z <  0 и z >  0 , соответственно.

Уравнение ПЭВ несложно получить из уравнений Максвелла

E ^{( 1} ) = x

i      f ' ^H

ik0 (£ 1 в2 ) I dz

H x¹ ) =

-

ik0 (e 1 -в2)

E ( ¹ ) = p. H ^{( 1} ) , y ¹ y ’

где

n =

£ 1П

I

rot H = - ik ₀ £ E , rot E = ik ₀ H ,

где k 0 = 2 n / % , % — длина волны в вакууме, и граничных условий непрерывности тангенциальных компонент полей при z = 0. Уравнение ПЭВ с направлением распространения p = ( а ₀ , в ₀ ) , | р| = 1 имеет вид

E ⁽¹) ( x , y , z ) = E ⁽¹) ( z ) exp ( ik 0 ( a x + P y ) ) =

= E⁽¹ ) ( z ) exp ( U^ ( ^a 0 x I P У ) ) ,

H ⁽¹) ( x , y , z ) = H ⁽¹) ( z ) exp ( ik ₀ ( a x + в y ) ) =

= H(1) ( z) exp (U^ (a0x I в y)) ,

где индекс I = m , d обозначает среду, k_SPP = k ₀ ^ £ _m £ _d /( £ _m +£ _d ) — константа распространения ПЭВ. Константы a , в в (2) удовлетворяют дисперсионному соотношению

^k 0² ( ^a 2 ^+в 2 ) = k SPP .

Выберем в качестве оптической оси ось Ox . В этом случае поле удобно описывать компонентой H _y , которая имеет вид

H y^d ) ( ^x , y , ^z ) = exp ( ^ik 0 ( ^{a x + e} y ) ) exp ( ^{- k} 0 Y d z ) ,

H ym ) ( ^x , y , ^z ) = exp ( ^ik 0 ( ^{a x +в} y ) ) exp ( k 0 Y m z ) ,

где

Y ² =a ² +в ² -£ i .                                (5)

Знаки в экспонентах от переменной z в (4) выбраны из условия затухания поля при удалении от границы. О стальные компоненты полей выражаются через H_y в виде

ez1) =

1       ( d H ^{( 1} )

ikrc^r^e1) I

I

+ ik 0 a H y )

J

H ¹ ) = 0,

I

- ik0 авп H(1) J

d H y¹ )

d z

I

+ ik ав H⁽ y ) J

' iав iав ) /f £dYd £mYm ) .£ d -в2 £ m -в2 J/ I £ d -в2 £ m -в2 J

Непосредственной подстановкой легко убедиться, что уравнения (4)–(7) удовлетворяют уравнениям Максвелла (1) и граничным условиям непрерывности тангенциальных компонент полей. В частном случае в = 0 из (4)-(7) следуют уравнения для ПЭВ, распространяющейся вдоль оси O x .

Обычно под ПЭВ понимают волну в виде (2), у которой константы а , в определены через компоненты единичного вектора направления ПЭВ p = ( а 0 , в 0 ) в виде

^k 0 ^{а k}SPP ^а 0 , ^k 0 ^{в k}5iPP ^в 0 . ⁽⁹⁾

При этом а, в — комплексные числа, поскольку диэлектрическая проницаемость металла £m является комплексной и величина kSPP также комплексная. В общем случае константы а, в должны лишь удовлетворять дисперсионному уравнению (3). В дальнейшем б удем использовать ПЭВ (4)–(7) при а = ^k^PP -k02в2/k0, ве R , (10) где R — множество действительных чисел. При действительных значениях в компонента Hy является ограниченной по переменной y и на границе раздела z = 0 имеет вид

H y ( x , y ,0 ) = exp ( ik ₀ в y ) exp I i^k SPP - k ^; p ^; x I .   (11)

Уравнение (11) позволяет получить для функ ции H_y на границе раздела z = 0 интегральные представления, аналогичные представлению поля через угловой спектр плоских волн и интегралу Кирхгофа, которые широко используются в скалярной теории дифракции [12, 13]. Действительно, запишем общее решение при z = 0 в виде суперпозиции ПЭВ

Hy (x, y ) =

= f I ( в ) exp ( ik ₀ в y ) exp I idk2_PP - k ₀2 p ² x I d p .

-^

При этом функция I ( в ) определяется через значения поля при x = 0 в виде

¹ ( ^в ) = Г ^Hy ( 0 , y ) exp ( ^{- ik} 0 ^в y ) dy .         ⁽¹³⁾

2n^J -~

Остальные компоненты поля могут быть получены из (6)–(8). Уравнение (12) полностью идентично интегральному представлению поля через уг ловой спектр плоских волн, используемому в скалярной теории дифракции [12, 13]. Уравнение (12) позволяет записать интеграл Кирхгофа для ПЭВ в виде

+^

H y ( x , y ) = j H_y ( 0 , u ) G ( x , y - u ) du ,          (14)

где

G (x, y ) = ko Г"

= -°-    exp

2n^J "

ikSPP x

2 s] x ² + y ^г

:S_PP - k 32 x j exp ( ik ₀ p y ) d p = (15)

^H 1 [ k SPP^ ^{x + y}

H\ (x) — функция Ханкеля первого рода, первого порядка [17]. Заменяя функцию Ханкеля асимптотическим выражением при больших значениях арг у-мента [17], получим

G (x, У) = ikSPP         x

2пx ² + y ² 4x ² + У ²

exp I ik_SPP^x ² + y у

Уравнения (14), (16) являются аналогами интеграла Кирхгофа в двумерном случае. Разлагая корень в (16), получим ядро интегрального преобразования для параксиального приближения Френ еля

G ( x , y ) =. Iik SPP exp ( ik spp x ) exp I ik SPP y 1 .      (17)

V 2nx     ^v ' I 2 x I

Уравнения (12), (13), (14), (17) использовались в [10, 11, 7] для моделирования электромагнитного поля на поверхности раздела сред. В [10, 11, 7] указанные интегральные представления использовались по аналогии со скалярной теорией [12]. Приведенные выше формулы являются строгим обоснованием указанных интегральных представлений.

Дифракционные оптические элементы для фокусировки ПЭВ

Для выполнения заданны х преобразований волновых полей широко используются фазовые дифракционные оптические элементы (ДОЭ) [18–20]. В скалярной теории дифракции прохождение падающей волны через ДОЭ описывается фазовой модуляцией входного волнового поля [21, 22]. Пусть выходная плоскость ДОЭ совпадает с плоскостью x = 0. При плоской падающей волне на выходе ДОЭ формируется поле с комплексной амплитудой w (0, у ) = A ( у )• exp (i ф( у )), (18) где A(y) — амплитуда падающей волны, φ(y) — фазовая функция ДОЭ. Фазовая функция φ(y) определяется высотой дифракционного микрорельефа h(y). Расчет фазовой модуляции, осуществляемой ДОЭ в каждой точке y, сводится к решению модельной за- дачи прохождения падающей волны через плоскопараллельную пластинку с толщиной h(y).

Наиболее часто эта задача решается в приближении геометрической оптики. В этом случае

ф( У ) =                 ) h ( у ),                    (19)

л где £b, £d — диэлектрические проницаемости материала ДОЭ и окружающей среды. Задача расчета ДОЭ ставится как задача расчета фазовой функци и ф(у) из условия формирования в некоторой области поля с заданными характеристиками, например, с заданной амплитудой или фазой [21, 22]. Для расчета ДОЭ разработано множество эффективных итерационных и аналитических методов [21, 22].

Пред став ленны й инт еграл Кирхгофа для ПЭВ (12)–(17) позволяет впрямую перенести методы расчета ДОЭ, используемые в скалярной теории, на расчет ДОЭ для преобразования и фокусировки ПЭВ. Рассмотрим прохождение ПЭВ, распространяющейся вдоль оси O x , через диэлектрический ДОЭ, расположенный на поверхности распространения (рис. 1). ДОЭ описывается функцией «длины» t ( у ) и изготовлен из материала с диэлектрической проницаемостью £ _b . Высоту ДОЭ в направлении оси z будем считать постоянной. Расчет поля за оптическим элементом в каждой точке y сведем к решению модельной задачи прохожд ения ПЭВ через диэлектрическую ступеньку с длиной t ( у ) . Геометрия модельной задачи прив едена на рис. 2. ПЭВ Н У 1 ) ( x ) = exp ( ik_SPPx ) в среде 1 падает на ступеньку слева, справа в среде 3 формируется выходная ПЭВ

^НУ^ ( ^x ) = T ) • exp ( ^ikSPP ( ^{x -} t ) ) ,

где t — длина ступеньки. Амплит уд у и фазу коэффициента пропускания T ₀ в (20) будем рассматривать как амплитудно-фазовую модуляцию, осуществляемую диэлектрической ступенькой длины t . При прохождении ПЭВ через диэлектрическую ступеньку часть энергии преобразуется в другие отраженные и прошедшие моды в средах 1 и 3.

В работе для решения задачи дифракции ПЭВ на диэлектрической ступеньке использовался метод Фурье мод [14–16]. Общая схема применения метода для решения данной задачи прив едена в [10]. В методе Фурье мод поле в средах 1, 3 представляется в виде суперпозиции мод

H y ^ ( x , z ) = exp ( ik_SPPx ) +

⁺ E R n exp ( ^ik 0 ^a - x ] V n ( z ) , n

H_ y ³⁾ ( x , z ) = T 0 exp ^ ik spp ( x - 1 ) ] +

⁺ E T n exp ( ^ik 0 ^a + ( x ^- t ) ] V n ( z ) .

n ^ 0

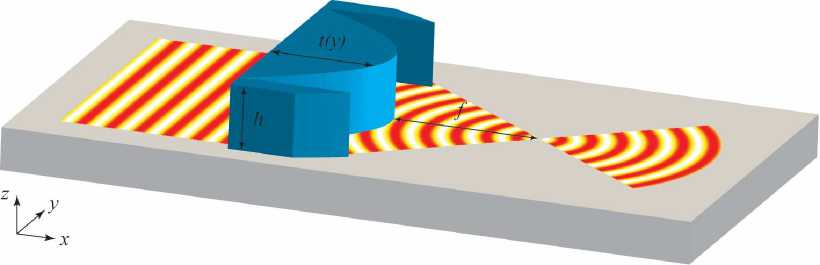
Рис. 1. Диэлектрический ДОЭ, расположенный на поверхности распространения ПЭВ

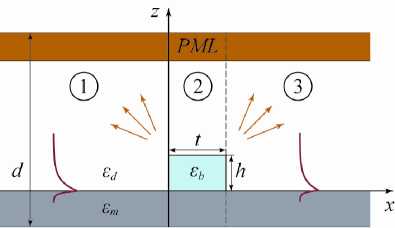
Рис. 2. Геометрия модельной задачи

Индексы ± у констант распространения а ± указывают знак их действительной части и определяют направления распространения мод. При этом знаки ± соответствуют распространению по оси Ox и против оси Ox , соответственно. Поперечные распределения мод в (21) представлены в виде отрезков рядов Фурье:

(2п )

V n ( z ) = S w exP I i , jz I .

• V         7

  
  

Константы распространения а ± и коэффициенты разложения w_nj в (22) определяются из решения задачи на собственные значения. Константы распространения а ± и коэффициенты w j являются собственными значениями и собственными векторами матрицы, состоящей из коэффициентов Фурье функц ии диэлектрической проницаемости [14, 15]. Периодическое представление поля по переменной z в (21), (22) соответствует периодической структуре. При расчетах фун кция диэлектрической проницаемости £ ( z ), | z | <  d /2 предполагалась периодичной с периодом d . Периодичность вводится специально для использования метода Фурье мод [15]. Для устранения в лияния межд у периодами на границах периода использовались согласованные поглощающие слои (PML–perfectly matched layers) [15, 23].

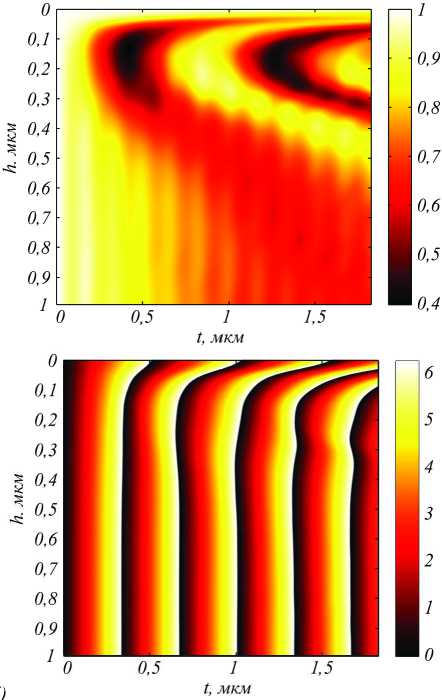
На рис. 3 приведены расчетные зависимости модуля и фазы коэффициента пропускания ПЭВ T ₀ от длины t и высоты h диэлектрической ступеньки.

Расчет производился при следующих параметрах: 1 = 550 нм, £ m =- 13,686 + 0,444 i , £ _d = 1, £ b = 2,25. Значение £ m соответствует диэлектрической проницаемости серебра при указанной длине волны.

а)

• б)

Рис. 3. Модуль |Т ₀ ( h , t )| (а) и фаза ф ( h , t ) = arg ( T₀ ( h , t ) ) (б) коэффициента пропускания диэлектрической ступеньки

Рис. 3 показывает, что зависимость фазы от длины ступеньки становится близкой к линейной при ув еличении высоты ступеньки.

При этом фаза начинает приобретать линейный вид при высоте h = 0,25 мкм. Глубина проникновения ПЭВ в среду 8 _d определяется как расстояние, на котором амплит уд а волны ум еньшается в e раз [24]. При указанных параметрах 8 _d = 0,13 мкм . Таким образом, зависимость становится квазилинейной при h = 2 8 _d , что соответствует уменьшению амплитуды ПЭВ в e ² раз. При h >  4 8 _d фаза хорошо описывается выражением

ф(t,h) = k0 ^m t = kSPPt, (23) Veb+ e m где kSbPP — волновой вектор ПЭВ в области ступеньки. Выражение (23) аналогично формуле геометрической оптики, используемой для набега фазы плоской волны через слой с толщиной t. Максимальное значение толщины ступеньки tmax = 1,67% на рис. 3 выбиралось из условия Аф(h) = (kSPP - kSPP)hmax = 2п . Это условие обеспечивает интервал разности фаз [0,2п] между ПЭВ, прошедшей через ступеньку с диэлектрической проницаемостью eb, и ПЭВ, распространяющейся в исходной среде. Введем функцию А(h, t) = arg(70(h, t)) - kSbPPt, характеризующую ошибку формулы (23) при фиксированном h. Максимальное значение ошибки А(h, t) при h = 1 мкм составляет менее п /17 . При расчете ДОЭ подобная ошибка в фазовой функции в большинстве случаев не является существенной [19, 20]. Модуль коэффициента пропускания при h = 1 мкм составляет более 0,7.

Линейная связь фазового набега с шириной диэлектрической ступеньки позволяет формировать заданные фазовые распределения за счет изменения длины ступеньки. Таким образом, для преобразования и фокусировки ПЭВ мог ут быть использованы дифракционные диэлектрические структуры с изменяющейся длиной и фиксированной высотой. Согласно (23), «длина ДОЭ» для формирования заданной фазовой функции ф ( у ) имеет вид

t ( У ) = Ф ( У )/( k SPP - k sPP ). (24)

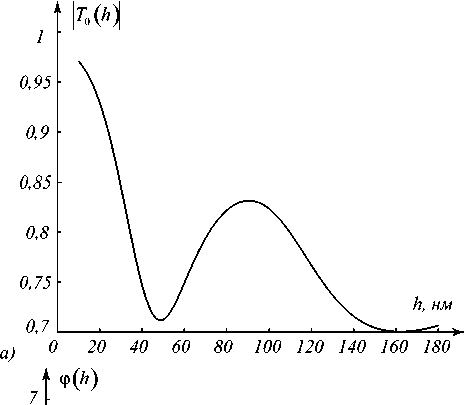
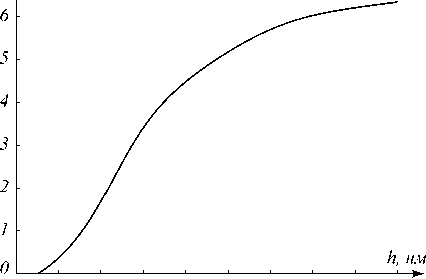
Рис. 3 показывает, что существует возможность изменения фазы прошедшей ПЭВ за счет изменения высоты ступеньки при фиксированной длине. В частности, на рис. 4 представлены зависимости мод уля коэффициента пропускания и фазы прошедшей ПЭВ от высоты ступеньки при фиксированной длине t = 1055 нм .

Рис. 4 показывает возможность фазовой модуляции в интервале [ 0,2 п ) при изменении высоты ступеньки от 0 до 180 нм. При этом модуль коэффициента пропускания составляет более 0,7.

• б)

Рис. 4. Зависимости модуля |7 0 ( h )| (а), и фазы ф ( h ) (б) коэффициента пропускания диэлектрической ступеньки от ее высоты при длине ступеньки t = 1055 нм

Таким образом, для преобразования и фокусировки ПЭВ могут быть также использованы диэлектрические структуры с изменяющейся высотой и фиксированной длиной (рис. 5).

Рассмотрим в качестве примера расчет линз ПЭВ с использованием мод уляции длины и высоты ступеньки. Согласно (14), (16), фазовая функция дифракционной линзы с фокусом f имеет вид

ф ( У ) = ^{- mod} 2 n ( R^e ( ^ksPP ) V У 2 ⁺ f 2 +Ф 0 ) ,     ⁽²⁵⁾

где ф ₀ — произвольная постоянная.

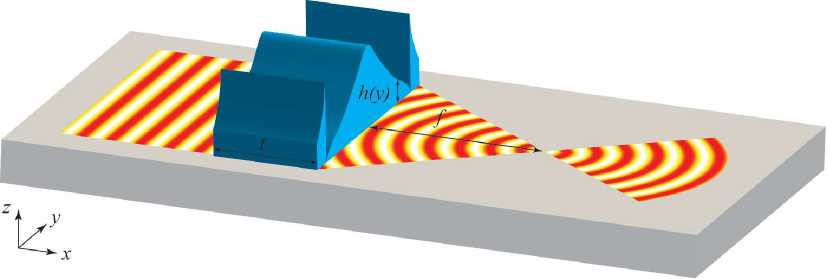
Рис. 5. Диэлектрический ДОЭ с изменяющейся высотой и фиксированной длиной

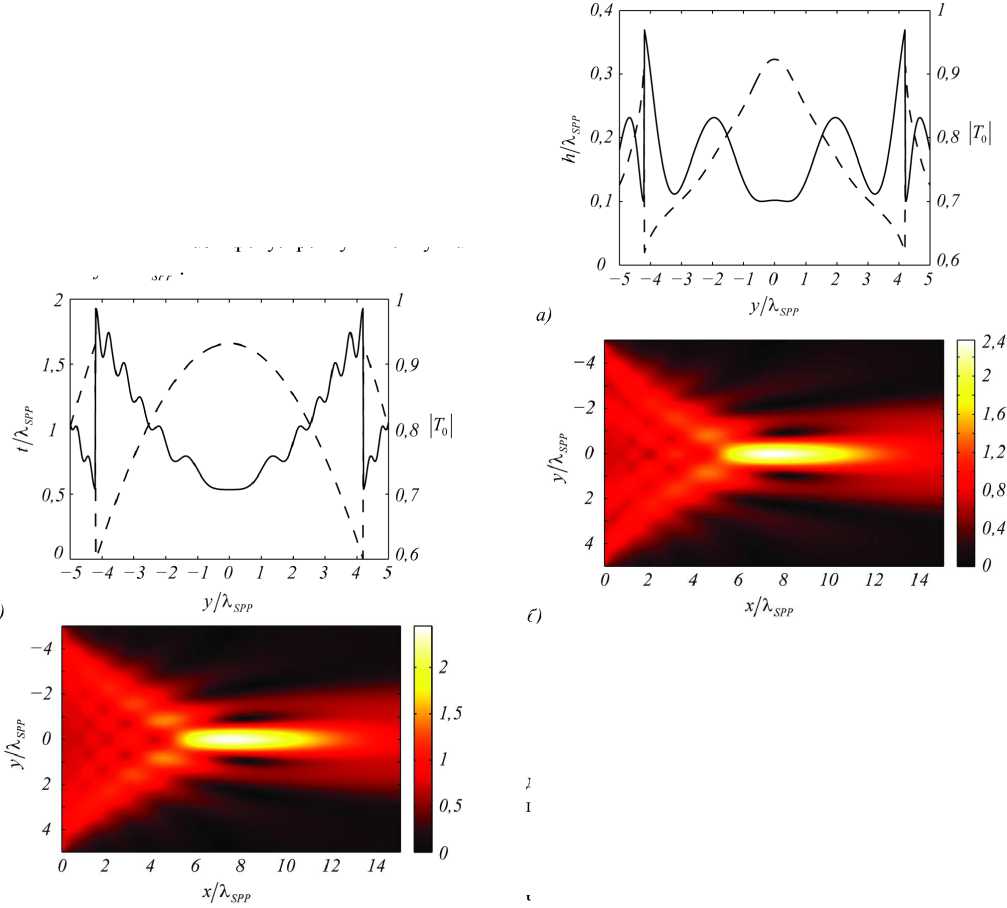
б)

Рис. 7. (а) Функция высоты, нормированная на длину волны ПЭВ (пунктирная линия) и функция амплитудного пропускания (сплошная линия) (а), формируемое распределение |H _y ( x , у )| (б)

На рис. 6а приведены ф ункц ии длины микрорельефа линзы и амплитудного пропус кания, рассчитанные при фокусе f = 8X_SPP и размере апертуры линзы 2 a = 10 Х _SPP . Длина микрорельефа нормирована на длину волны ПЭВ. Расчет длины проводился по формулам (24), (25). На рис. 6 б показано распределение величины \Н _у ( x , у )|, сформированное линзой и рассчитанное по формулам (14), (15). Рис. 6 б показывает фокусировку в точку на прямой x = f = 8Х_SPP .

б)

Рис. 6. Функция длины, нормированная на длину волны ПЭВ (пунктирная линия) и функция амплитудного пропускания (сплошная линия) (а), формируемое распределение |Н_у ( x , у )| (б)

На рис. 7 а приведены функции высоты микрорельефа линзы и амплитудного пропускания для линзы, рассчитанной при фиксированной длине ступеньки t = 1055 нм (рис. 5). Параметры линзы совпадают с предыд ущим примером.

Высота микрорельефа линзы была рассчитана численно из зависимости ф ( h ) , приведенной на рис. 4 б . Формируемо е распределение величины |Н_у ( x , у )| приведено на рис. 7 б и также показывает фокусировку в точку. Графики на рис. 6 б и 7 б близки по структуре.

Дифракционная эффективность линз была оценена по формуле [10]

+^

T e = 100 X

-^

k SPP

^^^^^^^

Re ( k SPP )

k oP 2 )

------d P (%). (26)

Дифракционная эффективность составила 60,5% для линзы, показанной на рис. 1, и 56,5% для линзы, показанной на рис. 5.

Заключение

Непосредственно из уравнений Максвелла получено интегральное представление электромагнитного поля на границе раздела сред через угловой спектр ПЭВ и интеграл Кирхгофа. На основе строгого решения задачи дифракции ПЭВ на диэлектрической ступеньке, расположенной непосредственно на поверхности распространения, показана возможность фазовой модуляции ПЭВ как за счет изменения длины ступеньки при фиксированной высоте, так и за счет изменения высоты ступеньки при фиксированной длине. С использованием указанных типов модуляции проведен расчет дифракционных линз для фокусировки ПЭВ. Дифракционная эффективность линз превышает 56%. Рассмотренные типы модуляции могут быть использованы для расчета дифракционных оптических элементов общего вида, рассчитанных с использованием подходов скалярной теории дифракции из условия выполнения заданных преобразований ПЭВ.

Способ фазовой модуляции ПЭВ мо жет быть обобщен. В ч астности, модуляция ПЭВ может быть о существлена за счет перфорирования по -верхно сти распространения системой прямо -угольных выемок субволнового размера.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE), гранта Президента РФ поддержки вед ущих научных школ (НШ-3086.2008.9), «Фонда содействия отечественной науке», грантов РФФИ № 09-07-92421, 07-0196602, 07-07-91580.