Расчет долговечности упорного шарикового подшипника при перекосе колец

Упорные подшипники работают, как правило, при невысоких скоростях вращения. В связи с этим в практических расчетах подшипников (см. [1]) не учитываются центробежные силы тел качения. Кроме того распределение нагрузки по телам качения принято оценивать в зависимости от эксцентриситета приложения осевой нагрузки. Эта величина условная, поэтому более целесообразно распределение нагрузки определять в зависимости от угла перекоса колец, который может быть установлен при деформациях и неточностях установки деталей подшипникового узла.

В настоящей работе излагается методика расчета однорядного упорного шарикового подшипника (см. рис.1) при перекосе колец.

Рис. 1. Однорядный упорный шариковый подшипник.

РАСЧЕТ ДЕФОРМАЦИЙ И СМЕЩЕНИЙ ПРИ ПЕРЕКОСЕ КОЛЕЦ

При компьютерных расчетах вычисление напряжений и деформаций в контактах шариков с кольцами выполняем по рекомендациям работы [3].

Приведенный модуль упругости в контакте определяется по зависимости:

Е пр = Е / ( 1 - Е² ) ^.

Здесь Е - модуль упругости, Е - коэффициент Пуассона для материала колец и шариков.

Приведенные радиусы кривизны в контакте определяются по формулам:

R y = D w R ! / 22R - D w ) - в направлении качения;

R x = D _WR/ ( 2R - D _w ) – в направлении, перпендикулярном направлению качения.

Здесь: D w – диаметр шарика; R - радиус желоба кольца; R 1 - радиус в контакте кольца в направлении качения.

Как показано на рис. 2, радиус в контакте кольца в направлении качения при угловом контакте шарика с желобом может быть определен по формуле:

R ₁ = D0/2sin a + R .

Здесь: D 0 – диаметр по центрам радиусов желобов колец; a - угол контакта шарика с желобом.

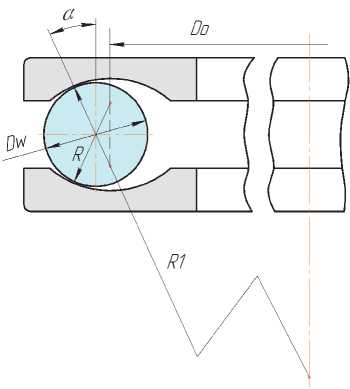
Рис. 2. Схема углового контакта шарика с желобом

При отсутствии углового контакта (при а = 0) радиус R 1 равен бесконечности и принимается R y = D wF .

Вспомогательный коэффициент

Y = 1 - ( 1 - R y R ^ .

Безразмерные коэффициенты для расчета:

k ₆ = 1,0401 • Y⁰² - деформаций;

k p = 0,2295 • Y⁰¹⁸⁹ - напряжений;

k =(146641Y0’0945 YRJr °318 - боль-a           xy шей полуоси площадки контакта;

0 0945          0 318

kb =(7,4184/1 ’   ДRy Rx ) - меньшей полуоси площадки контакта.

Приведенная кривизна в контакте шарика с желобом определяется по формуле:

Р пр = 41 D w - 1^ 1 - 1/R .

При отсутствии углового контакта (при а = 0) радиус R 1 равен бесконечности и принимается Р пр = 4,D „ - 1/R.

С использованием приведенных коэффициентов формулы принимают вид:

6 = k ₆ 3 ( F)E _пр ) ² р _пр - для расчета деформаций;

ст Н = к_р 3 F ( Е_прр_пр ) ² — для расчета напряжений;

а = кa VF/(Eпр Рпр ) и b = kb^F/EEпр рпр ) - для расчета размеров большей и меньшей полуосей площадки контакта.

Смещения колец в упорном подшипнике без перекоса определяется только деформациями в контактах шариков с кольцами. Величину смещения можно определить равенством: S a = 2 6 . При этом при расчете деформации нагрузка в контакте шарика с кольцом может быть принята равной F = F_a/z , где F a - осевая нагрузка на подшипник, z – число шариков.

При перекосе колец смещения в сечениях по каждому шарику будут различными. Схема смещений для минимально нагруженного шарика при перекосе показана на рисунке 3.

Величина смещения будет зависеть от угловой координаты шарика, показанной на рис. 4.

Принимая, что ось поворота кольца проходит через центр желоба в сечении максимально нагруженного шарика, расстояние от оси поворота до центра желоба в сечении любого шарика с координатой ф = 2 ^ ( i - 1)/z определится по формуле:

l = D 0 ( 1 - cos ф)/2 .

Тогда смещение колец в сечении данного ша-

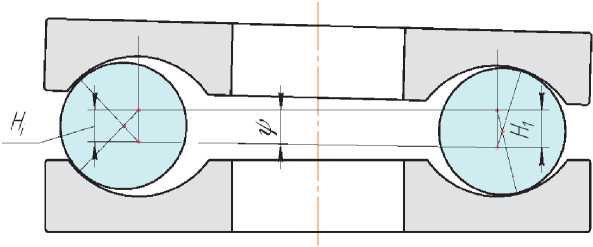
Рис. 3. Схема смещений колец при перекосе

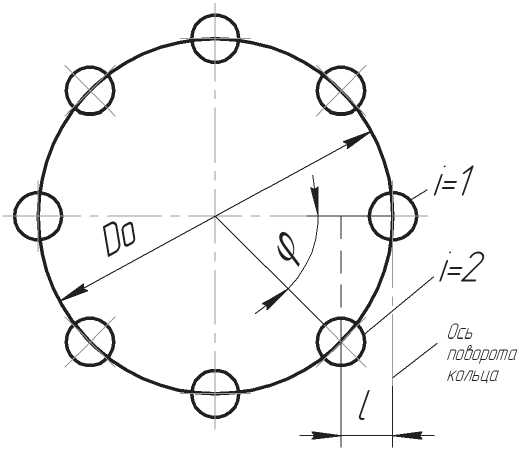
Рис. 4. Угловая координата шарика при перекосе рика будет равно:

S i = S 1 - D 0 ( 1 - cos ф ) sin ^ 2 .

Здесь: S 1 – смещение в сечении максимально нагруженного шарика, ^ - угол перекоса колец.

Величины смещений будут определять нагрузки в контактах шариков в каждом сечении.

РАСПРЕДЕЛЕНИЕ НАГРУЗКИ МЕЖДУ ШАРИКАМИ ПРИ ПЕРЕКОСЕ КОЛЕЦ

Схема сил, действующих на шарик в любом произвольном сечении, показана на рисунке 5.

Условие равновесия шариков без учета сил трения имеет вид:

^2Fi^si n ^a i = Fa .

Здесь F ci – центробежная сила шарика.

Геометрические соотношения в сечении можно записать в виде:

Hi = 2R - Dw + Si =

( 2R - D w + 2 6 i ) cos a i .

Здесь ⁶ i = k ^ 1^ ⁽ F i /^Епр ) ^р прi .

Полученная система уравнений решается численно методом последовательных приближений. В качестве начального приближения принимаем величину деформации 6 0 из условия равномерного распределения нагрузки.

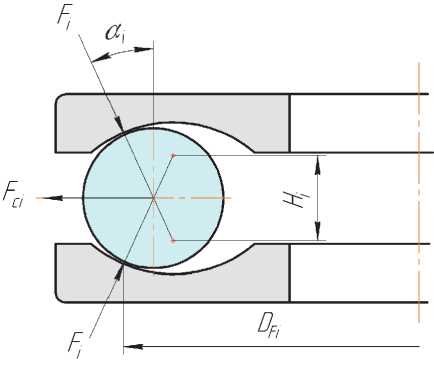
Рис. 5. Схема сил, действующих на шарик

Определяется соответствующее значение угла контакта:

a i = arccosy

2R "  D w + S i 2R - D w + 2 S q

Затем уточняются значения k ^ , P _n pi и F ci , определяются значения усилия в контакте по формуле F i = F ci / 2 sin a i , а также уточняется величина деформации S i .

Если обеспечивается с заданной точностью равенство деформаций S i и S q , расчет закончен. Иначе корректируется величина S q , и расчет повторяется.

Условие равновесия кольца имеет вид:

z

Ф( S1 ) = Fa - Z Ficosai = 0.

i = 1

Для решения этого уравнения задаёмся начальным значением смещения S 1 из условия равномерного распределения нагрузки между шариками. Определяются, как показано выше усилия в контактах всех шариков и проверяется условие равновесия кольца.

При невыполнении этого условия вводится поправка в значение S 1 и расчет повторяется.

При выполнении условия равновесия кольца выполняются проверки условий невыхода шариков на кромки желобов и прижатия шарика центробежной силой к сепаратору. При выполнении указанных условий определяется действующий на кольцо опрокидывающий момент по формуле:

М опр = Z F i D Fi ^{cos a} i ^cos ^ ² . i = 1

Здесь D Fi - диаметр расположения центра площадки контакта данного шарика с желобом, определяемый по формуле:

DFi = Dq + 2 (R - Si) sin ai.

Упорные подшипники, как правило, тихоходные, поэтому при расчетах центробежными силами пренебрегают. Вместе с тем при перекосе колец часть шариков будет разгруженной или мало нагруженной. Тогда центробежные силы вызовут их смещение в радиальном направлении, что приведет к угловому контакту шариков с желобами [5]. Возможно взаимодействие шариков с сепаратором или выход шариков на кромки бортиков желобов.

Для расчета центробежной силы примем, что окружная скорость центра шарика V 0i будет определяться, как показано на рис. 6.

Скорость в контакте шарика с желобом вращающегося кольца определим по формуле:

Vi = ( Dq + 2R sin ai ^)^ 2, где to = nn!30 - угловая скорость вращающегося кольца.

Окружную скорость переносного движения шарика можно определить по формуле:

^V0i = ^D0wi ^to 0i I² .

Здесь: to Qi - угловая скорость переносного движения шарика, D 0wi – диаметр окружности по центру рассматриваемого шарика, который может быть определен по зависимости:

D owi = D q + ( 2R - D w ) sin a i .

Принимая V Qi = V i 1 2 , с учетом выше приведенных соотношений получим:

to    Do + 2R sin a

to0i =---7-------H---

2 D q + ( 2R - D w ) sin a i ^.

Центробежную силу шарика определим по формуле:

Fci = mwDowitooip, где mw – масса шарика.

В зоне разгруженных шариков возможно прижатие шариков центробежными силами к сепаратору, как показано на рис. 7.

Это может вызвать смещение сепаратора, дополнительные нагрузки на его перемычки и скольжение шариков.

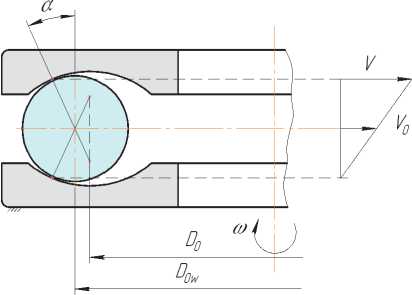
Рис. 6. План скоростей шарика

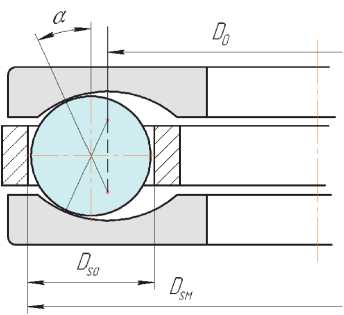
Рис. 7. Схема прижатия шарика к сепаратору

На рис. 7 имеем диаметр окружности, охватывающей шарики в рабочих условиях, определится выражением:

Dsm — Do + (R - DwP + Siz) sin«i-

^{+ (} R ^- D _w[ 2 ⁺ S i ⁾ sin « i ⁺ D w *

Здесь S i и S iz - деформации в контактах а « 1 и a iz - углы контакта максимально нагруженного шарика и противоположного ему соответственно.

Номер шарика, противоположного максимально нагруженному, определится выражением iz — int ( z/2 ) .

Если D_sm >  D o + D so , где D so - диаметр отверстия гнезда сепаратора, следует увеличить диаметр отверстия гнезда.

При отсутствии контакта с гнездом сепаратора возможно выкатывание в разгруженной зоне шарика на кромку бортика желоба, как показано на рис. 8.

Предельное значение угла контакта шарика с желобом определяется выражением:

« пред ^{— arcsin ( Ь}ж 2R ⁾ , где b ж – ширина желоба.

С учетом деформаций в контактах условие невыхода площадки контакта на кромку бортика определится выражением « i + P i <  « пред .

Величина P i в радианах определяется по

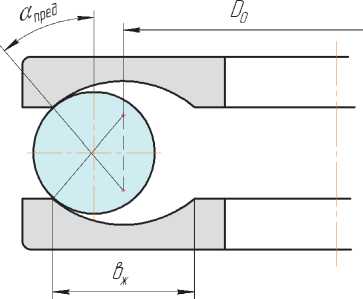
Рис. 8. Выкатывание шарика на кромку бортика желоба формуле Pi- ai/R, где ai - размер большей полуоси площадки контакта шарика с желобом.

Для определения запаса невыхода вычисляется расстояние от кромки бортика до площадки контакта по формуле: