Расчет двумерной вероятности снижения трудоемкости со сжатием цикла изготовления сложных изделий в условиях роста производительности труда

При запуске в серийное производство прогнозируемая трудоемкость (Tj ) изготовления головного изделия может быть определена по формуле

Т, = К^ \/ ³6+d₇ + d₈>k₉, (1) где: ^К^Л^Лз^ - коэффициенты группы уравнений, моделируемых на ЭВМ; (G^ -масса пустого самолета; ^N₅ - количество условно изготовленных изделий от начала серийного производства; (^) - некорректируемая доля трудоемкости; \d₇i - доля машинного времени заводского оборудования; (dg^j - доля трудоемкости изготовления обшивки самолета; (к₉ - коэффициент, учитывающий прирост производительности труда по формуле

_        100 _______

9 "" 100 + 0,4-к10 -1П ’        (2)

где: (к₁₀^ -среднегодовой темп прироста производительности труда; Qu - количество лет, истекших от базового года запуска головного изделия в серийное производство; (О,4^ -доля, относящаяся к трудовой деятельности основных производственных рабочих.

В выражении (1) трудоемкость (1) ) прямо пропорциональна величине показателя (к₉ } при постоянстве прочих переменных. Данная величина имеет смысл коэффициента снижения трудоемкости изготовления изделия. Она зависит от величины (N₃ ), которая не входит в состав формулы (2). Время QjQ) течет для всех одинаково. Поэтому доля Q),4^ подрезает показатель (к ₁₀ . В условиях стагнации предприя-

тия при отрицательном значении \к₁₀) показатель (к^ в формуле (1) увеличивает трудоемкость производства, что приводит к абсурду статистическую отчетность предприятия.

Уравнение (1) определяет величину единственного ресурса ^7^. В математическом отношении данное уравнение является аналогом так называемой производственной функции Кобба - Дугласа, где множество условных переменных неявно влияют на величины других ресурсов предприятия. Например, при дефиците рабочей силы объем производства продукции прямо пропорционален дефитному ресурсу. Функция Кобба - Дугласа теряет связь с сопряженными ресурсами предприятия. Роль ее неявных переменных величин сводится к нивелированию иных ресурсов, избыточных по отношению к данному дефициту, что способствует утечке невостребованного капитала.

Запишем Q1 — к₁₀^ в форме десятичной дроби и приведем подобные члены в выражении (2)

к g

1 + a-tu '

зателя

Представим часть выражения (1) без пока- Qk^ в форме параметра ((/ .

Ф = КГ G12 • N< 3 (d6 + d7 + d8)

Соотношение (1) принимает вид потенциальной функции

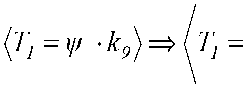
V \ l + a.t

Известные в прошлом процессы производства и распространения изделий в стихии рыночной экономики могут быть представлены случайными для будущего развития предприятия ордина- тами (Z7 (х2), Z2 (х2),..., Zm Дт ^, аппроксимиро ванными графиком кривой уравнения Перла

ДУДу'/Дх^

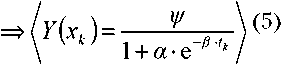
где: («,Д^ ) - параметрыаппроксимации кривой; (/) -время, приуроченное к оси Д^ абсцисс графика; /_у (^ ) -функция плотности вероятности;

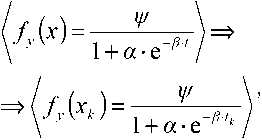
где: (/^у и \Хь) индексы времени и вероятности fy\x_k); (к = 1,2,3,„,тУ

Таким образом, в моменты времени Upt^,... дД случайные значения ^2; (х_; ), Z₂ (х₂ ),... , Z_m (x_m )) коррелируются величинами функции:

^УД; )=V • Л-fo)., Y(х₂) = у . / (х₂), ...ЛДтЛУ-ЛК)

Статистическая гипотеза относительно уравнения (5) в единстве его аппроксимирующих параметр в Др, у у, заключается в том, что значения непрерывной функции У (х ) в моменты времени Д, t,,... , t_m ) признаются математи-че-скими ожиданиями случайных величин Д1 Д1 X ² 2 (^2 X ••• - ^Zm Д_т )) при (а >  0 , 0 и к = 1,2,..., ту . При этом формула (5) есть уравнение регрессии, а ординаты У (х_; X Y^Xi X - ^ Дт ) являются независимыми случайными величинами в соответствии с теоремой об умножении вероятностей

т

Из тождественности выражений (4) и (5) следует

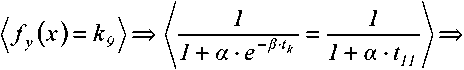
^^е-^ =1_к^Д P-e = lnty (7)

Находим первую и вторую производные от первообразной (7)

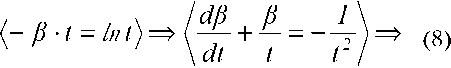
Id² р 1 dp Р _ 1 \ ^V^l'd! Г "21=]^ Воспользуемся разложением в ряд ^ при условии, что ( bi t < «о у             '

int , bit bP tbi"

7/    21ml

Исходя из выражения Д р -t = 1шу находим соотношение t = 1 - р ■ t +

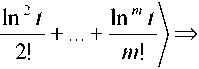
In² 1

В t = 1 - 1 +

In³ 1

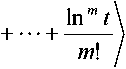
Запишем производную первого и второго порядка от данной первообразной

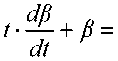
In /

11-1.

In2/ In”'"1/

-I---1-----H -.-------------?;

2/ • t pn -1)/ • t d2 p dp / 1 Int \ dr2     dt \ll-t- 11-Pj

/ In /     In² 1 \

+ (------^---— ) -I---- w*f2 ibt- lnm~4 In""2/

Дт- 2)/ -P (m - 2)/ • P

In"'"²/        In™"¹ 1 \

(т-2ур Уп-Д.-Р]

После приведения подобных членов производная второго порядка имеет вид d2 р 2 d р _ 1 d t2 t d t t"

Вычтем из выражения (10) выражение (9)

dfl р^_£__1_ dt t t² 2t²'

Запишем интеграл в форме решения задачи Коши для линейного неодно-родного уравнения первого порядка

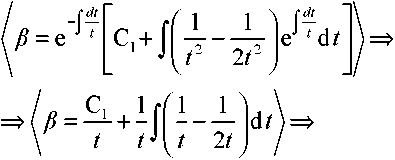
Определим потенциал (Z7 предприятия, достаточный для изготовления головного изделия

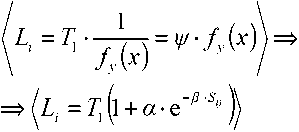
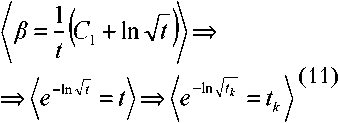
Функция (12) относится к экспоненциальному виду распределения случайных величин, ограниченных С ОДНОЙ стороны (О < f_y (х ) < оо У Функции данного вида называются Марковеки-

При (t_k = 1^ из соотнощения (И) следует, что постоянная интегрирования (Cf = 0^ . Функция J_y (х ) принимает вид

ми, т.к. они характеризуются отсутствием последействия. Т.е. будующее состояние f_y \X_k+I)

в момент времени состояния f_v U, )

зависит только от ее

в настоящий момент

и

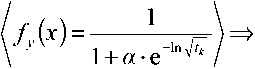
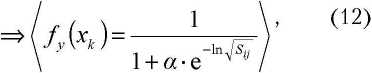
где: \8у) - спефицированный индекс серийно-госчета; (i = 1,2,.... S) - индекс серии однородных в конструктивном отношении изделий; (S) - количество серий; О — 1,2,...N^ - индекс изделия i-mой серии; \Nj - количество изделий в г-той серии. Таким образом, содержащийся в исходном выражении (5) индекс (t^ замещен специфицированным индексом J* J), которому соответствует вероятность f_y ^Хъ ) из области распределения вероятности f_y (^) в моменты времени (t₁, t₂,..., t_m ) относящиеся к планируемому периоду.

Исходя из выражения (5), определяем (у/ = ty где <^Д - внутренний потенциал предприятия, т.к. его способность изготовить и реализовать (8^ серию изделий требуемого качества и в заданный срок, определяемый темпом роста производительности труда и количеством заказанных изделий.

не зависит от ее состоянии fy (^ )’ fy Iх 2 \- fy Jk-i ) в прошлом.

Наличие у марковских функций двумерной вероятности показывает на то, что функция fy (х ) является проекцией вектора / (х ) на ось ординат. Следовательно, существует проекция /^(х) вектора f (х) на ось абсцисс. Данные проекции связывает угол (у) наклона гипотенузы, который зависит от серийного счета изделий у = у0 + arcctg

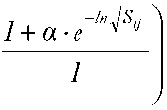
Для головного изделия

(S_n -t^^ lyy₁ = arcetgQ + oc^ . Из этого условия находим начальный угол уу₀ = К/4^ наклона вектора f\X) и величину его модуля l/wv?

7Г (₇ —/nJsJ

+ ^cct^l + а • е

Таким образом получается, что в зависимости от серийного счета изделий функция (14) имеет смысл коэффициента снижения трудоемкости изделия

Г =

— /nJ Sj •

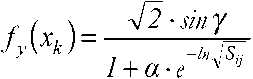
На основании предшествующего опыта, потенциал (L _t ^ может быть формально представлен внутренними ресурсами фондов рабочей силы требуемой квалификации и машинного времени заводского оборудования. Стало быть, потенциал (ly не включают внешние ресурсы кооперированных поставок узлов, агрегатов и готовых изделий сторонних производителей, т.к. затраты на их поставку переносят сборочным процессом из состава оборотных средств предприятия на себестоимость готовой продукции.

Функция (15) имеет смысл коэффициента сжатия производственного цикла изготовления изделия

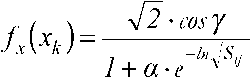
На рис. 1 приведены результаты расчета коэффициентов (k_3>k_6ik₁₀^ снижения трудоемкости изделия и коэффициентов сжатия

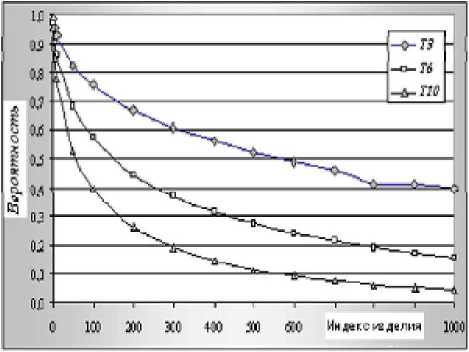
Рис. 1. Вероятность снижения трудоемкости от в зависимости от темпа роста производительности труда

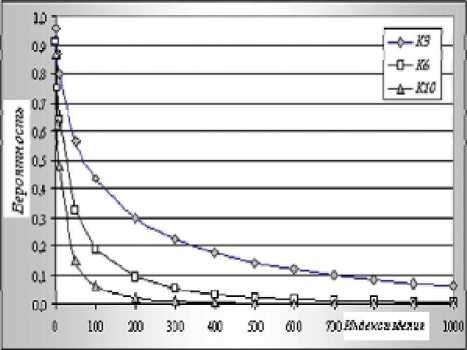
Рис. 2. Вероятность сжатия цикла изготовления изделия в зависимости от темпа роста производительности труда

^₃,^_б,^_]0 производственного цикла изготовления изделий при темпах роста производительности труда (а₃ = 3%,а₆ = 6%,а₁₀ = Ю^/о) , соответственно. В данном примере все изделия включены в одну серию

Таким образом, разработана двумерная функция для расчета вероятности снижения трудоемкости и сжатия цикла изготовления изделий применительно к серийному производству Данная функция является исходным пунктом для развертывания цепей условных вероятностей в составе САПР технологического планирования и технической подготовки производства.