Расчет фрагильности стекол с помощью уравнения Вильямса-Ландела-Ферри

Автор: Машанов А.А., Сандитов Д.С., Мантатов В.В., Сандитов Б.Д., Викулина Л.С.

Журнал: Вестник Бурятского государственного университета. Философия @vestnik-bsu

Статья в выпуске: 6, 2007 года.

Бесплатный доступ

Получена формула, связывающая фрагильность стекол с параметрами уравнения Вильямса-Ландела-Ферри. Она находится в согласии с данными фрагильности свинцовосиликатных и натриевоборатных стекол. Для этих стекол установлена зависимость фрагильности от решеточного параметра Грюнайзена - меры энгармонизма колебаний квазирешетки.

Короткий адрес: https://sciup.org/148178160

IDR: 148178160

Текст научной статьи Расчет фрагильности стекол с помощью уравнения Вильямса-Ландела-Ферри

получена формула, связывающая фрагильность стекол с параметрами уравнения Вильямса-Ландела-Ферри. Она находится в согласии с данными фрагильности свинцовосиликатных и натриевоборатных стекол. Для этих стекол установлена зависимость фрагильности от решеточного параметра Грюнайзена - меры ангармонизма колебаний квазирешетки.

Calculation fragility glasses by means of the equationWilliams- Landel-Ferry1

In this paper we discuss the relationship between fragility and coefficient of transverse deformation of glass and present a method to calculate fragility of glasses with Williams-Landel-Ferry equation.

Обобщение данных по вязкости различных стекол в координатах \^-\т{т^ приводит к выводу о том, что “прочные” (“strong”) стекла, например SiO?, в этих координатах имеют меньшую вогнутость кривых, чем “хрупкие” (“fragile”) стекла, в частности молекулярные солеподобные [1]. Различным аспектам такой классификации стекол посвящена серия работ (см., например, [1-3]).

В данном сообщении рассматривается взаимосвязь между фрагильностью и ангармонизмом колебаний квазирешетки стекол.

Фрагильность определяется тангенсом угла наклона кривой ^-(г/г) вблизи температуры стеклования т^ [1]

(О

Температурная зависимость вязкости 7(/Л вблизи температуры стеклования удовлетворительно описывается уравнением Вильямса-Ландела-Ферри [4]

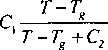
где _Дг=₇(7^,)/>7(Г_е), С} и С₂ - эмпирические постоянные, которые в рамках модели возбужденного состояния [5, 6] имеют следующий физический смысл

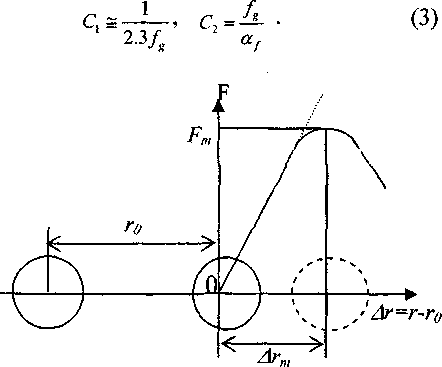
Рис. 1, Схема возбуждения атома. г₉ - среднее межатомное расстояние, Дг_т - критическое смещение атома, соответствующее максимуму силы притяжения F_m.

Здесь f_g - объемная доля флуктуационного объема, замороженная при температуре стеклования

(УД

/ = ~ % const * 0.02 - 0.03 .

X /?<7, af- температурный коэффициент доли флуктуационного объема f(T) при Т8.

В модели возбужденного состояния [5, 6] предполагается, что в жидкостях и аморфных средах существуют возбужденные кинетические единицы (атомы, группы атомов), способные сместиться на критическое расстояние дг„, соответствующее максимуму силы межатомного (межмолекулярного) притяжения Fm (рис. 1). В качестве «возбужденного атома» в силикатных стеклах выступает мостиковый атом кислорода в фрагменте кремнекислородной сетки Si-O-Si, а в линейных аморфных полимерах - небольшой участок основной цепи макромолекулы (группа атомов в повторяющемся звене). Данная модель основана на обобщении концепции свободного объема [4, 7, 8].

Флуктуационный объем стеклообразующей системы обусловлен критическими смещениями возбужденных атомов из равновесных положений [5, 6]:

vf где Ne - число возбужденных атомов, птг-площадь эффективного сечения атома. В свою очередь, критическое смещение атома, или предельная деформация межатомной связи Дгт, оказывается функцией па раметра Грюнайзена у - меры ангармонизма [9]

= —. (4)

^ бу

Следовательно, вследствие проявления нелинейности силы межатомного взаимодействия при значительном смещении кинетической единицы из положения равновесия (рисЛ) флуктуационный объем v_f и его доля f_g зависят от ангармонизма колебаний межатомных связей [10]. Величина f для многокомпонентных силикатных стекол и ряда аморфных полимеров линейно растет с увеличением ангармонизма (у). Для халькогенидных стекол наблюдается, наоборот, уменьшение^ сростом у [11]. Так что нет общей закономерности изменения функции ^,(у) для различных стекол. Важно то, что доля флуктуационного объема f_g определенным образом зависит от ангармонизма колебаний межатомных (межмолекулярных) связей.

Легко убедиться, что применение в соотношении (1) уравнения Вильямса-Ландела-Ферри (2) для зависимости р(Т) позволяет связать фрагильность pt с эмпирическими параметрами данного уравнения

СТ т = (5)

Таблица. Расчет фрагильности свинцовосили-катных, натриевоборатных стекол по формуле (5) из данных о температуре стеклования и параметрах уравнения Вильямся-Ландела-Ферри С, и С₂.

Содержаний окисло, мол. %	Т„, К	с,	С₂.К	m=£5L с.	т (1)	fs
РЬО	РЬО - SiO₂
20	808	19	543	28.4	30	0 023
30	765	21	501	32.9	33.3	0.02
33.3	749	22	490	34.4	34.4	0.019
35	746	30	688	32.8	34.4	0.014
40.1	728	27	562	35.2	35.7	0.015
42.1	702	34	660	35.9	-	0.012
45	697	18	333	38.8	38.8	0.023
48	675	33	552	40.9	42	0.013
49.6	675	22	301	50.2	46.6	0.019
50	673	50	856	39.7	43	0.008
55	646	81	1272	40.9	43.4	0.005
60	640	188	2780	43.1	43.4	0.002
63	632	93	1180	49.6	51.8	0.004
66	618	26	262	60.5	53	0.017
66.6	619	26	263	62.1	-	0.016
68	627	49	559	55	55	0.009
70	627	16	499	58.1	57	0.026
73	606	-208	-244	51.6	56	-0.09
Na₂O	Na₂O - В₂О₃
2.8	565	18	269	37.5	37.5	0.024
5.4	571	22	367	33.9	376 4	0.019
8	573	24	394	34.7	41.2 5	0.018
10.7	616	20	335	37.5	38.4 6	0.021
13.5	642	20	309	42.3	42.8 6	0.021
15.3	663	29	456	42 4	46	0.015
17.5	663	20	265	49	48	0.022
19.5	717	77	1174	46.9	53.4	0.005
20.2	717	38	549	50	54.1	0.0 Н
213	727	40	574	51.2	56.4	ООН
23.2	733	21	256	60.2	57.5 8	0.021
24.3	733	21	253	60.2	59.3 7	0.021
25.9	734	26	346	55.9	57.5	0.016
27.4	739	22	261	64.1	62.5	0.019
29.8	737	20	229	65.3	64	0.021
32.6	739	20	216	69.9	68.4	0.021
35.4	739	21	228	67.6	69.1	0.021
38.5	733	23	24]	70.9	70.5 8	0.019

Расчет т по этой формуле из данных о величинах С/, Су и T_g находится в удовлетворительном согласии с непосредствен-

102 ным определением фрагильности по формуле (1) (табл.)

При подстановке в данное равенство С-и С2 из соотношений (3) и при использовании приближенного выражения «^^111(1/.^) [7] фрагильность оказывается функцией доли флуктуационного объема при температуре стеклования msWA>. (6)

Таким образом, из модели возбужденного состояния следует, что фрагильность m через функцию^/) зависит от ангармонизма - параметра Грюнайзена у.

Величину у можно рассчитать из данных о коэффициенте Пуассона ц [9, 12]

* - 2^ J

Как и следовало ожидать, у свинцовоси-ликатных и натриевоборатных стекол наблюдается вполне определенная зависимость фрагильности от параметра Грюнайзена (рис. 2 и 3). Экспериментальные данные о вязкости и коэффициенте Пуассона брали из справочника [13]. При росте содержания окиси свинца РЬО с 20 до 70 мол.% увеличивается примерно в 2 раза фрагильность (с 30 до 60) и параметр Грюнайзена (с 1.2 до 2.3). У этих стекол т в первом приближении линейно возрастает в зависимости от роста ангармонизма (рис. 2).

У натриевоборатных стекол наблюдается своеобразная зависимость фрагильности от параметра Грюнайзена (рис. 3) При росте содержания NaiO с 2,7 до 22,8 мол.% ангармонизм падает с у = 2.1 до y = L9, а фрагильность растет с 35 до 55. При дальнейшем росте содержания Nc^O с 24,2 до 37 мол.% фрагильность натриевоборатных стекол линейно растет с увеличением параметра Грюнайзена, как у свинцовосили-катных стекол.

Таким образом, между фрагильностью и ангармонизмом стекол существует определенная взаимосвязь, что может быть качественно обоснована в рамках модели возбужденного состояния.

Список литературы Расчет фрагильности стекол с помощью уравнения Вильямса-Ландела-Ферри

Angell C.A. Perspective on the glass transition//J. Phys. Chetn.. Solids. -1988. -V. 49. -N 8. -P. 836-871.
Sokolov A.P., Rossler E., Kisliuk A, Quitman D. Dynamics of strong and fragile glassformers: differences//Phys. Rev. Lett. -1993. -V. 71. -P. 2062-2065.
Novikov V.N., Sokolov A.P. Poisson's ratio and the fragility of glass-forming liquids//Nature. 2004.-V.431.-P.961-963.
Ферри Дж. Вязкоупругие свойства полимеров. -М.: ИЛ, 1963.-535 с.
Сандитов Д.С. Условие стеклования жидкостей и критерий плавления Линдемана в модели возбужденного состояния//Докл. РАН. -2003. Т. 390.-№2.-С. 209-213.
Сандитов Д.С. Модель возбужденного состояния и вязкоупругие свойства аморфных полимеров и стекол//Высокомолек. соед. А. -2005. _ Т. 47. -№3. -С. 478-489.
Сандитов Д.С., Бартенев Г.М. Физические свойства неупорядоченных структур. -Новосибирск: Наука, 1982. -259 с.
Френкель Я.И. Кинетическая теория жидкостей. -М.,Л.: Изд-во АН СССР, 1945. -424 с.
Сандитов Д.С., Козлов Г.В., Ангармонизм межатомных и межмолекулярных связей и физико-механические свойства полимерных стекол//Физика и химия стекла. -1995. -Т. 21. -№ 6. -С. 549-578.
Сандитов Д.С., Сангадиев С.Ш. Новый подход к интерпретации флуктуационного свободного объема аморфных полимеров и стекол//Высокомолек. соед. А. 1999. Т. 41. № 6. С. 9771000.
Мельниченко Т.Д., Ризак В.М., Мельниченко Т.Н., Феделиш В.И. Параметры теории флуктуационного свободного объема в стеклах системы Ge-As-Se II Физика и химия стекла. -2004. -Т. 30. -№ 5. -С. 553-564.
Сандитов Д.С., Дармаев М.В., Сандитов Д.С., Мантатов В.В. Коэффициент поперечной деформации и ангармонизм колебаний решетки квазиизотропных твердых тел//Высокомолек. соед. А. -2007. -Т. 49. -№ 6. -С. 213 -219.
Мазурин О.В., Стрельцина М.В., ШвайкоШвайковская Т.Н. Свойства стекол и стеклообразующих расплавов. Справочник. -Т. 1. -Л.: Наука, 1973.-444 с.

Еще

Статья научная