Расчет гидродинамических параметров рабочей решетки центробежного насоса

Входные кромки лопаток рабочего колеса (РК) центробежного насоса (ЦБН) оказывают подтормаживающее действие на поток, а, следовательно, его формирование. Пограничные слои, образующиеся на поверхностях входной кромки, не только управляются потоком, но и оказывают на него обратное влияние через толщину вытеснения δ^* и потери импульса δ^** (рис. 1). Для определения этого влияния рассмотрим составляющие сил, действующих на входную кромку лопатки и их удельный вклад в баланс потерь энергии при течении вязкой жидкости в рабочей решетке ЦБН.

Выражение для касательного напряжения τ на ограничивающих поверхностях рабочей решетки РК определим, воспользовавшись табличной функцией f ₂ ( x ) работы [1]:

f 2 ( x ) =

**

δz ⋅τ0

.

νρ W _{( x )}

Согласно [1] скорость потенциального течения в ядре потока в решетке профилей можно записать в виде

W ( j ) = Cj^m , (2) где С и m – постоянные величины, здесь

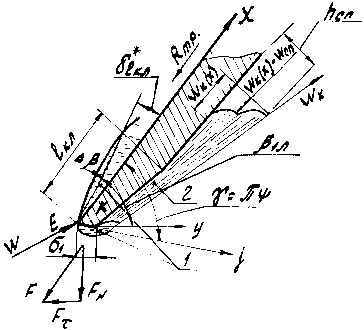
Рис. 1. Расчетная схема обтекания входной кромки лопатки потоком вязкой жидкости:

1 – ламинарный пограничный слой; 2 – спутное течение

Ψγ m==  .

2- Ψ 2π-γ

При формировании входной кромки лопатки, совместимой с осью Y (γ = β 1л ),

m=

^β 1л 2 π-β 1л .

Для лопатки на расстоянии, равном σ 1 , от входной кромки, при j = σ 1 ; W ( j ) ≈ W к имеем

w

C = ^{W к} , σ 1 ^m

и выражение (2) получим в виде

w

W ( j ) = ^W _m ^к j ^m .                  (6)

σ 1 ^m

Величина касательных напряжений при обтекании решетки профилей входной кромки, согласно выражению (1), с учетом (6) будет составлять

Решив уравнение для напорной стороны лопатки, получим значение силы трения:

_ Р^{V f} 2 ( $ )

^T 01 ^_      **

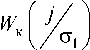
² Р ^f 2 ( $ ) W 3v ml f x f _ т dx _----^7. ----- —

^T x 0 ^{01 (} x )       ( 3 m + 1)\ $ V l

3 m + 1

или

где 5 ** - толщина потери импульса, которую выразим в виде [1]:

(5 *'f _ $ V djL .             (8)

⁽ 1 )     dW ( j )                   ' '

F t l

_ 2 p f 2 ( $ ) W 3 V ml

( 3 m + 1 ) V $

.

Тогда выражение (7) получим в виде

2 m

С ^j )

или

^Т 01 ^_

æ dj

W 3 v m j ^т 01 =Р f 2 ( $ )J 1 7 $ с 1 V/

Интегрированием выражения (9) получим значение силы трения по кромке лопатки рабочей решетки:

j

^F t ( . j )=Ь 1 (. j ) ^dj =

² Р f 2 ( $ ) W 3 v m C ( 3 m + 1 ) V     $

^{f j}/ 1 (10) vc )

Величина силы трения, определяемая вязкостью жидкости по входной кромке лопатки длиной σ1, бу-

Следует отметить, что конечная толщина лопатки и параметры ее входной кромки не только формируют поток на входе рабочей решетки профилей, но и оказывают на него подтормаживающее действие за счет силы реакции F и стесняющее действие за счет конечной толщины 5 _л с суммарной площадью лопаток на входе, соизмеримой с проходным сечением решетки.

Полную силу F , действующую на поток со стороны кромки, можно разложить на две составляющие: F_N – нормальную к входной кромке и F _τ – касательную, которая представляет собой силу трения, определяемую вязкостью жидкости. Сила F N вычисляется согласно закону распределения давления вдоль входной кромки лопатки величиной σ₁:

^с 1

F n _ J Pdj .                   (14)

дет иметь вид

F

TC 1

² Р f 2 ( $ ) W^ v m C i ( 3 m + 1 ) V    $

При различной кинематической вязкости от 0,7·10–6 м2/с до 1·10–4 м2/с и плотности сила трения вдоль входной кромки лопатки возрастает и тем больше, чем выше вязкость рабочей жидкости (рис. 2).

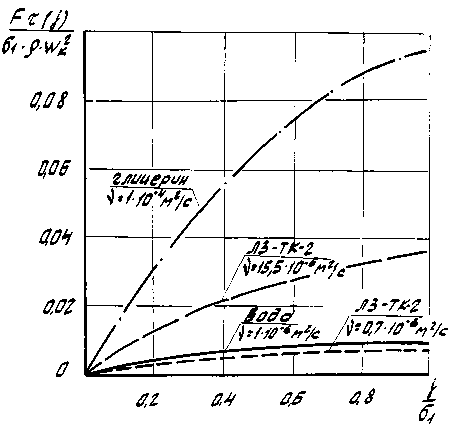
Рис. 2. Изменение параметров пограничного слоя рабочей решетки профилей вдоль входной кромки лопатки

Для определения силы F_N (рис. 1), нормальной к входной кромке лопатки, согласно выражению (14) имеем:

^с 1           ^с 1

F n _ J Pdj _ J ( P 1 - Р к ) dj + Р к C 1 .        (15)

Запишем уравнение энергии потока в рабочей решет-

ке в виде

Р 1 - Р к _Р

(Wк2 - W2)

тогда

Р

² к

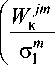
F  1 PW

F N ^_ J 0 2

P W ?-J

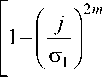
Р W ^

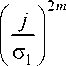
^{dj + Р} к ^C 1 ^_

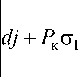
Р W к² _   2 m

C1            .

2    1 2 m + 1

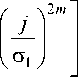
Ламинарный пограничный слой, образовавшийся на входной кромке лопатки величиной δ1, затем стекает к тыльной поверхности и распространяется по длине канала аналогично плоскому спутному потоку (рис. 1). Ламинарное спутное течение, как правило, неустойчиво, так как в нем профили скоростей имеют точку перегиба и поэтому оно переходит в турбулентное [1; 2].

Экспериментальные данные по изучению картины течения в РК [3] показывают, что даже в высокоэффективных РК имеется зона отрыва, которая к выходу из РК распространяется на 15–30 % по шагу канала. Спутная струя вдоль тыльной стороны лопатки характеризуется в [4] постоянным значением скорости Wсп по шагу с величиной 20–30 % от среднерасходной скорости основного потока.

Анализ фотографий и визуализация течений по тыльной стороне лопатки РК ЦБН позволили уточ- нить картину течения и создать расчетную модель, позволяющую оценить границы спутного потока и учесть его влияние в общем балансе потерь энергии [3].

При течении вязкой жидкости за входной кромкой лопатки образовавшийся ламинарный пограничный слой при обтекании уступа величиной ст1 =

V / sin Р 1л

срывается с поверхности профиля (точка К на рис. 1). За точкой отрыва распространяется зона спутного потока вдоль тыльной стороны лопатки. Согласно [1], граница расширяющейся спутной струи и толщина зоны смешения двух плоских струй несжимаемой жидкости принимается изменяющейся пропорционально расстоянию l ( x ) от начальной точки К:

dh сп = ± C1 - Wk dl (x)      1 + Wk , где

- W

Wk = — к сп

.

По опытным данным Б. А. Жесткова и др. [5], значение константы С для начального участка плоской струи рекомендуется принимать равным 0,27, что хорошо согласуется с нашими опытами по визуализации [3].

Опытами О. В. Яковлевского, Б. А. Жесткова и др. показано в [1], что при Wк ≥ 0,4 течение спутного потока характеризуется независимостью угла раскрытия зоны спутного потока от отношения скоростей. При этом расчеты основного участка спутного течения, исключающего образование циркуляционной зоны, ограничиваются значением Wок ≤ 3, что соот- ветствует условию постоянства статического давления по длине струи.

Следует отметить, что при существенно больших

W значениях W = — линии тока в спутном потоке к Wсп существенно искривляются, отражаясь на характере течения канала. Возникает картина течения с обратным током [3]. Это связано с тем, что вследствие смешения струй, имеющих скорости Wk >> W,п, образуется положительный градиент давления, приводящий к особенно сильному торможению струи меньшей скорости. Возможно полное ее торможение с образованием замкнутой циркуляционной зоны [3].

Для основного участка спутного потока принимаем, что профиль скорости состоит из отрезков профилей струйного пограничного слоя и пограничного слоя на стенке, причем сопряжение этих профилей осуществляется на границе пристеночного слоя при у = 5 ( ^ 1 ) . Для турбулентного на стенке пограничного слоя принятое распределение скоростей подчиняется закону «одной седьмой»

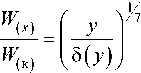
где W _к – скорость на границе пристеночного пограничного слоя с толщиной 5 ( у ) .

Значения параметров l ( x ) н и h сп.н соизмеримы с толщиной пограничного слоя S ( c 1 ) потока, обтекающего клин, и основной вклад в характеристики спутного потока вносит основной участок, длина которого не менее чем на два порядка больше начального и переходного участков.

Рассмотрим влияние изменения давления в потоке на основные свойства зоны турбулентного смешения. Г. Н. Абрамовичем [5] показано, что в случае малости толщины зоны смешения h сп l ( x ), ей присущи все особенности пограничного слоя, в частности, можно пренебрегать изменением давления по толщине зоны смешения спутного потока. Таким образом, в зоне смешения струй профили скорости не зависят от радиального градиента давления, так как на границах струйного пограничного слоя конечной толщины полученные градиенты скорости равны нулю и профиль скорости соответствует безградиентному течению.

С учетом градиентного течения основного потока параметр утолщения зоны спутного потока запишем, согласно решению [5], в виде dhсп dl (x)

= C

1 - ^сп

1 + W осп

W осп

^^^^^B

^{l (} x )

dP

dl ( x )

2P где P =---— - приведенное давление, величина ко

Р Wo2k торого определяется в зависимости от градиента давления по длине канала, P = f(l(x)).

Интегрированием уравнения (20) при граничном условии на носике лопатки, в точке К l ( x ) = 0 и h сп = 0 получим выражение для расчета толщины спутного потока.

Радиальному градиенту давления будет сопутствовать обязательное от центра РК радиальное движение жидкости на обеих границах зоны смешения ( W _сп ^ 0

и W _K * 0). При этом величина

dP

dl (x)

в рабочей ре-

чение, при котором происходит полное торможение потока ( W _сп = 0) на границе зоны смешения:

шетке РК не должна превышать определенного значения, приводящего к полному торможению спутной струи и образованию вихревого обратного течения в решетке профилей РК по тыльной стороне лопатки.

Из уравнений Бернулли, связывающих местную скорость и давление в потенциальной части потока для струй одинаковой несжимаемой жидкости (ρ = const),

dP

dl (x)

l ( x ) = W оСп -

Скорость спутного потока для течения вдоль входной кромки лопатки длиной σ1, совпадающей с осью Y (см. рис. 1), аналогично выражению (6):

получим

W in - W 2n = W k² - W 2 ,          (21)

w

Woc n =  "K ym - осп jm

или

² к

² ок

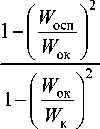
1 — Ween сп

При обтекании лопатки с клинообразной входной кромкой, совпадающей с осью Y , с учетом выражений (3) и (4), для потока, стекающего с входной кромки лопатки длиной σ 1 на ее тыльную поверхность (точка К на рис. 1), отношение скоростей спутного и основного потоков выразим формулой

Для образования вихревого обратного течения в спутном потоке достаточно условие W _сп = 0. Тогда (22) будет иметь вид

w

осп

w осп

w ок

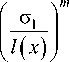
m

= C j .

или

W к       2

2   1 Wосп, ок

Величина повышения давления в зоне смешения

2 ( P - P o ) P W o2

осп .

потоков будет

2 ( P - P o ) P W k²

2 m

G i .

Откуда наибольшая величина повышения давления

в зоне смешения потоков определяется по выражению

2 ( P — P o ) P W o2K

осп .

Величина давления по тыльной стороне лопатки, при котором в канале РК формируется вихревой поток, составит

^P ' ⁽ x ) = W - P o-^ - P o - ⁽²6)

Например, при W _осп = 1 прирост давления в зоне смешения не может превышать скоростного напора струи основного потока, имеющего большую скорость [2; 5].

Зависимость местного отношения скорости W _сп на границах зоны смешения от градиента давления по длине рабочей решетки РК, используя [5], выразим

Из указанных зависимостей вытекает, что при работе РК с лопатками конечной толщины на вязкой и невязкой жидкостях характеристики зоны спутного потока зависят от соотношения величин входной кромки и длины лопатки, заданного градиента давления по длине зоны смешения, максимальная величина которого определяется уравнением (31).

Величину относительной скорости спутного потока из уравнения (27) выразим

2 m

^C i

dP

осп

dP

сп

сп

dl (x)

l(x)

dP

-----/ . l ( x ) dl ( x )

.

Откуда следует, что при положительном градиенте

dP давления > 0 имеет место его предельное зна-dl (x)

dl (x)

l ( x )

dP

----l ( x ) dl (x)

.

dP

При = 0 полученное выражение соответст- dl ( x )

вует безградиентному обтеканию профиля лопатки и согласуется с известными зависимостями [5].

Решение полученных уравнений позволяет определить изменение относительной скорости спутного потока ( W _сп ) при градиентном обтекании тыльной стороны рабочей решетки лопатки, границы зоны спутного потока h сп в зависимости от относительной скорости набегающего потока W _осп при различных значениях как угла натекания потока (β 1 ), так и относительной длины входной кромки лопатки ( C 1 ). В результате найдены границы и оптимизированы условия, при которых в решетке РК реализуется спут-

ное безвихревое течение, что обеспечивает наилучшие энергетические характеристики. На рис. 3 приведены зависимости наибольшего значения dP

W _сп = f      без образования вихревых и обратных

dl (x)

зон в рабочей решетке с тыльной стороны лопатки при изменении величины ( ^ т ) от 0 до 1, что соответствует изменению угла натекания потока от 0 до 90°.

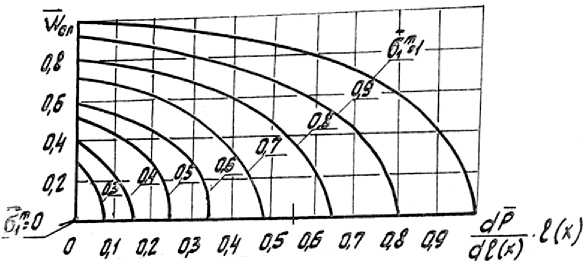
Рис. 3. Зависимость относительной скорости спутного потока в рабочей решетке РК от относительного перепада давления при различных углах натекания потока

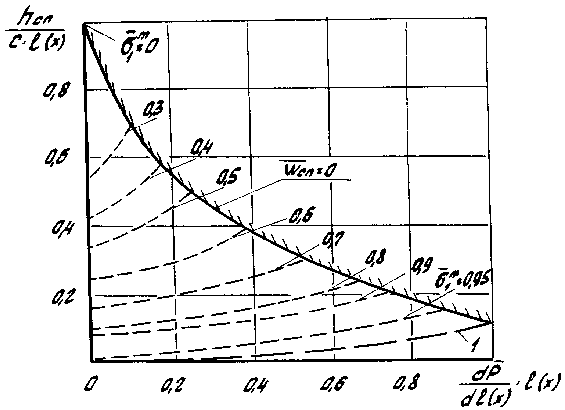
Рис. 4. Расчетное значение границы спутного потока при W _сп = 0

При предельных значениях угла β_1л в первом случае (β 1л = 0°) поток касателен к окружности канала лопаток (^ = 1), а во тором - перпендикулярен (^ = 0), что соответствует течению на кромках лопаток как при обтекании уступов и впадин. Показательно, что с ростом угла установки профиля рабочей решетки относительная величина наибольшего значения перепада давления уменьшается. В противном случае в решетке лопаток РК реализуется вихревое течение с отрывом потока по тыльной стороне лопатки .

Расчетное значение параметров спутного потока во всем диапазоне изменения угла установки, соотношения входной кромки и длины лопатки приведены на рис. 4 (пунктирные линии).

Полученные зависимости ограничены кривой, соответствующей критическому соотношению скоростей основного и спутного потоков: W _сп = 0. При этом режиме за счет нарастания давления в основном потоке спутная струя тормозится до нуля и дальнейшее нарастание давления в рабочей решетке центробежного насоса приведет к вихревому течению с отрывом потока по тыльной стороне лопатки.