Расчет гофрированной стенки на прочность и жесткость аналитическим и численным методами

Гофрированные стенки используются в трансформаторах для компенсации избыточного давления масла при нагреве. Гофрированная стенка под давлением имеет ограничения в условиях эксплуатации. Деформации ее гофр в общем случае должны быть упругими и не допускающими схлопывания.

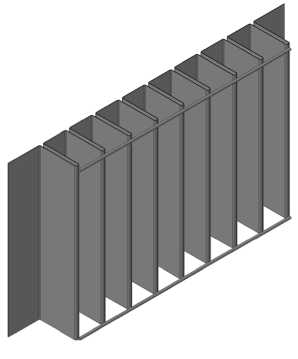
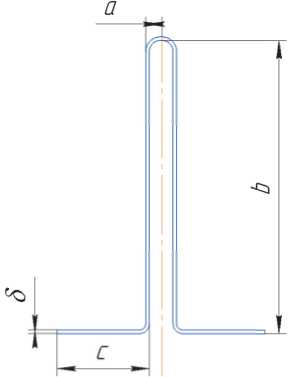
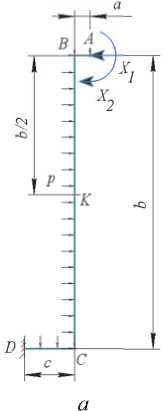
Гофр представляет собой тонкостенную конструкцию, полученную гибкой листа (рисунок 1, а). Геометрические параметры гофра, необходимые для расчета, приведены на рисунке 1, б.

В качестве расчетной схемы гофра используем конструкцию в виде рамы с прямоугольным сечением ^ ^х 1- Учитываем симметрию гофра относительно вертикальной оси (рисунок 2, а). Имеем статически неопределимую систему. Определяем неизвестные реакции в скользящей заделке X ₁ и X ₂ методом сил [1]. Расчет напряжений и перемещений гофра проводим в упругой линейной постановке. Схемы, используемые в этих расчетах, приведены на рисунках 2, б-д.

Записываем систему канонических уравнений метода сил:

'5_U X + 5 12 X ₂ +Д 1 p = 0 ;

5 ₂₁ X + 5 22 X 2 + Д ₂ p = 0 ,

³ M ¹ M ^{1              3} M ¹ M ²

где 5ii = ZJ —— dxi, 512 = 52i = ZJ       dxi, i=1 li EI                         i=1 li EI

3 M 2 M 2        3 M p M 1

522 = Z J        dxi, Д1 p = Z J _ dxi , i=1 li EI                   i=1 li EI

³ M^pM ²

Д^р = Z J------“xi - определяются с помощью p м li EI i интеграла Мора.

Выражения изгибающих моментов от заданных внешних нагрузок и от единичных нагрузок по 3-м участкам рамы представлены в таблице1.

На основе интеграла Мора

М ¹ " ¹ ,1      1 l2 /b

⁵'цХ 1 !■ Ы ^dx Ы^Ь ( s ⁺ 4

5i2 = 52i = Zf^iJ, ""^x^—Z(^+bc), l Ы           Ы 2 J

" ² " ² ,      1

^ 22 = X l-1 X -ЦТ" ^dxi =77 ( ^ + b + c ) , l Ы1             Ы1

^ _1T = f "r"dx = -^-(0,25a ² b ² + 0,125b ⁴ + Ы Ы

+0,5b(a² + b²)c + 0,5ac ² b + ^ c³b),

^ 2p = f "г" ^x ^^- C^a ³ + 0,5a ² b + ¹b ³ +

Ы Ы о         о

+0,5(a² + b²)c + 0,5ac² + ^ c³) .

Складывая оба уравнения канонической системы метода сил, предварительно умножив первое уравнение системы на Д₂ 1 , а второе на

-5 11 , получим неизвестную реакцию X 2 5 12 ^ 21 ^ 2 ⁺ ^ 1р⁵21 ^{— 5}22⁵11 ^ 2 ^— ^ 2р⁵11 = ⁰ ,

У _ ^2р⁵11 ^— А 1р⁵21

Д2 = Т ё ё ё ■

512521   511522

Складывая оба уравнения канонической системы метода сил,предварительно умножив

a

б

Рис. 1. Гофрированная стенка: а - общий вид; б - сечение рассчитываемой части гофра

Таблица 1. Выражения изгибающих моментов от заданных внешних нагрузок и от единичных нагрузок по 3-ем участкам рамы

Участок	Mp	M1	M 2
AB	M 1 p = — 0 , 5 px 2	M ] 1 = 0	M 2 = 0
BC	M 2 = — 0 , 5 pa 2 — 0 , 5 px 2	M 2 = 1 • x = x	m 2 = — i
CD	M з =— 0 , 5 p ( a 2 + b 2 ) — pax — 0 , 5 px 2	M ] = 1 • b = b	M ] = — 1

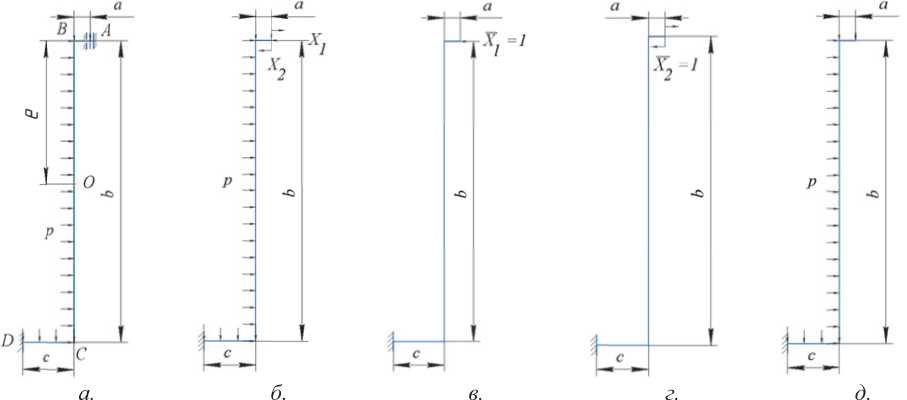
Рис. 2. Расчетная схема гофра, представленного в виде рамы:

а – статически неопределимая рама; б – эквивалентная система метода сил;

в – основная система, нагруженная единичной силой; г – основная система, нагруженная единичным моментом; д – основная система, нагруженная заданной распределенной нагрузкой

первое уравнение системы на б ₂₂ , а второе на —5₁₂ , получим неизвестную реакцию X 1

^ 11 ^ 22 ^ 1 + ^ 1р ^ 22 ^— ^ 21 ^ 12 ^ 1 ^— ^ 2р ^ 12 ^— О,

В точке А: M A = - X 2 , a A =

6 M A

^ _ ^ 2р ^ 12 ^— ^ 1р ^ 22 ¹   ^ 11 ^ 22 ^— ^ 12 ^ 21

■

где 5 - толщина гофра.

В точке B: M B = - X 2 - 0,5 pa ² , a B

6 M B

5 ² .

Определяем изгибающие моменты и напряжения в точках A, B, C, D (рисунок 2, а).

В точке C: M C = X 1b - X 2 - 0,5 p ( а^г + b ² ) ,

6 M

° - = ^2 -

исходит в середине BC стенки гофра (точка K). Определяем прогиб с помощью интеграла Мора:

В точке D:

M D = X 1 b - X ₂ - 0,5 p ( a 2 + 2 ac + b 2 + c 2 ) ,

6=ij MM i=1 li     EI

dx ,

6 M D

°D

Определяем экстремальное значение изгибающего момента на участке рамы BC в точке O:

M (x) = X1 x - X2 - 0,5p (a2 + x2), dM (x)

—-— = 0, X. - px = 0, x = —, dxp где x – расстояние от начала участка BC до сечения, где действует экстремальный изгибающий момент на этом участке.

Определяем экстремальный изгибающий момент:

MO = X1 x-X2 -0,5p(a2 + x2), где Mi – аналитическое выражение изгибающего момента от заданных нагрузок в произвольном сечении на каждом i-ом участке рамы;

Mi – аналитическое выражение изгибающего момента от единичной нагрузки P = 1 в том же т 63

сечении, 1 = — - момент инерции, E1 - жест- кость сечения балки при изгибе.

Расчетная схема определения перемещения точки K_п редставлена на рисунке 3.

Выражения изгибающих моментов от заданных внешних нагрузок и от единичных нагрузок по 4-м участкам рамы представлены в таблице 2.

Подставляем выражения изгибающих моментов в формулу интеграла Мора:

° o =

6 M O

6 k =

Наибольший прогиб стенки BC гофра про-

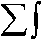
i = 1 i

M • M л

— --ddx = -

EI

5 X ₁ b ³ X ₂ b ²

48     8

EI

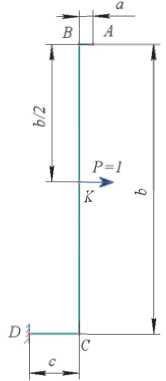
Рис. 3. Расчетная схема для определения перемещения точки К гофра

Таблица 2. Выражения изгибающих моментов от заданных внешних нагрузок и от единичных нагрузок по 4-ем участкам рамы

Участок Mi Mi AB M = -X2 - 0,5px2 M = 0 BK M = X,x-X2 -0,5pa2 -0,5px2 M = 0 KC M = X, (x + 0,5b)-X2 -0,5pa2 --0,5 pb (0,25b + x) - 0,5 px2 M = -1 • x = - x CD M = X!b - X2 - pa (0,5a + x) --0,5pb2 - 0,5px2 M = -1 • 0,5 b = -0,5 b pa2b2 17pb4   X1b2c X2bc pa2bc

----1-------

16     384     2      2      4

pabc ²   pb ³ c pbc ³

.

4      4     12

Наряду с аналитическим расчетом выполняется численное моделирование рамы методом конечных элементов для одного расчетного случая. Исходные данные, выбранные для расчета: p = 1 кг/см² – внешнее давление, а = 44 см, b = 10 см, с = 3,06 см – геометрические параметры гофра, указанные на схеме (рисунок 1, б), Е = 2 ^. 10⁶ кг/см²– модуль продольной упругости материала гофра, v = 0,3 - коэффициент Пуассона, 5 = 0,12 см – толщина стенки.

Результаты численного расчета приведены на рисунках 4, а-б.

Результаты аналитического и численного расчетов сведены в таблицу 3. Приведенные результаты показывают хорошее совпадение зна- чений напряжений и перемещений, полученных предложенными методами.

Максимальный прогиб стенки гофра в рассмотренном расчетном случае не превышает половину расстояния между его стенками 0,38 см, следовательно, соприкосновение стенок гофра не происходит.

Задача решается как физически линейная с учетом только упругих свойств материала гофра. В случае допустимости пластических деформаций расчет должен производитьсяс учетом геометрической и физической нелинейностей численными методами.