Расчет границ радиационного и теплопроводного режимов дугового разряда

При постановке и выполнении исследовательских задач, практическом использовании дуговых разрядов может быть полезна информация о параметрах газоразрядной плазмы и степени воздействия различных физических факторов на ее состояние. На параметры плазмы наибольшее влияние оказывают энергетические механизмы, от вклада которых зависят распределения температуры и электропроводности, другие характеристики разряда. В свою очередь, соотношение мощности энергетических механизмов определяется параметрами процесса: силой тока, давлением, геометрическими размерами, транспортными и радиационными свойствами рабочего газа. Для случая стационарной дуги, ограниченной цилиндрической стенкой, определенного газа и заданного давления характеристики разряда зависят прежде всего от силы тока I и радиуса стенки R 0 . В данной статье по результатам расчетов структуры разряда и характеристик энергетического баланса в широком диапазоне значений силы тока и радиуса стенки определены на плоскости I – R 0 границы радиационного и теплопроводного режимов и соответствующие им значения максимальной температуры для дугового разряда в воздухе, аргоне и углекислом газе. Работа является развитием исследований [1, 2], в которых рассмотрены особенности формирования структуры дугового разряда в воздухе и определены границы радиационного режима.

Постановка задачи

Рассмотрим электродуговую плазму, находящуюся в состоянии локального термодинамического равновесия, при атмосферном давлении данное приближение применимо при силе тока I ≥ 10 А [3]. Тепловыделение в электропроводном газе обеспечивается за счет джоулевой

Распределение температуры в разряде, горящем в цилиндрическом объеме и имеющем осевую симметрию, описано уравнением Эленбааса-Хеллера следующего вида:

+ qJ - qR = °, где r – радиус, T – температура, qJ = σE2 – мощность джоулевой диссипации, qR – объемная мощность радиационных энергопотерь, X и а - коэффициенты теплопроводности и электропроводности газа, E – напряженность электрического поля.

Уравнение (1) дополняется граничными условиями в центре разрядной области

-= О

- r = 0

и на внешней границе

[T ] r=R 0 = T0.

Напряженность электрического поля зависит от силы тока и распределения электропроводности по радиусу

R ₀

E=12. 0-■ -(4)

Электрические дуги, как правило, имеют поперечный размер, не превышающий нескольких сантиметров, и малую оптическую толщину В этом случае излучение имеет преимущественно объемный характер. Так, в работе [5] было показано, что учет переноса излучения в виде лучистой теплопроводности начинает оказывать какое-либо заметное влияние на характеристики разряда в аргоне при атмосферном давлении только при температурах свыше 15 000 К. С учетом этого в данной математической модели для расчета радиационных энергопотерь было использовано приближение объемного излучателя [1].

Реальные газы имеют сложные нелинейные температурные зависимости теплофизических свойств, что обусловливает необходимость применения численных методов. Решение краевой задачи (1)-(4) проводилось с помощью конечноразностного алгоритма, величина пространствен -ного шага в расчетах принималась равной 0.5 мм. Коэффициенты черноты воздуха взяты в [6], [7], аргона в [5], углекислого газа в [7], транспортные свойства воздуха в [8], аргона в [9], углекислого газа в [10]. Температурные зависимости свойств газов вводились в программу в виде таблиц для степеней черноты ε( T ), коэффициентов электропроводности σ( T ) и теплопроводности λ( T) с максимальным значением температуры T = 20 кК (для аргона 17 кК) и шагом Δ T = 1 кК.

Результаты расчетов

Вычислительная модель позволяет рассчитать структуру разряда для разных газов при различных значениях силы тока I и радиуса расчетной области R 0 . Из решения уравнений – 184 –

(1) - (4) определялось распределение температуры и рассчитывались напряженность электрического поля E , удельные и интегральные энергетические характеристики дугового столба. Напряженность электрического поля является важным параметром, характеризующим энергобаланс в разряде, поскольку она определяет величину мощности джоулевой диссипации, компенсирующей теплопроводные и радиационные энергопотери. На рис. 1 и 2 приведено сопоставление вольтамперных характеристик (ВАХ), полученных из экспериментов и с помощью данной математической модели. На рис.1 представлены расчетные и экспериментальные [11] значения E при атмосферном давлении в воздухе (свободно горящая дуга) и углекислом газе (радиус канала 2 см). На рис. 2 для аргона при атмосферном давлении и двух значений радиуса канала (2.5 и 3 мм) сопоставлены данные измерений [12] и расчетов, которые в этом случае были проведены при величине разностного шага 0.1 мм. И эксперимен-

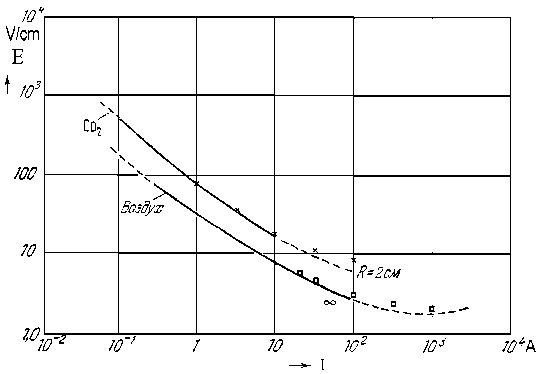
Рис. 1. Экспериментальные ВАХ и расчетные значения E (квадратики для воздуха, крестики для СО₂)

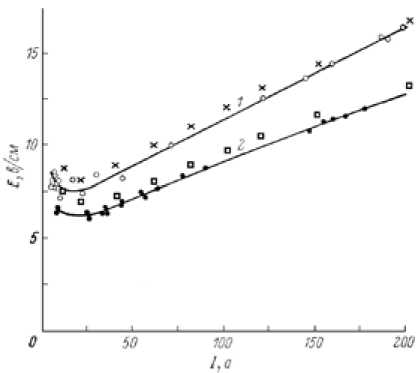
Рис. 2. Экспериментальные ВАХ и расчетные значения E для аргона (кривая 1 и крестики для R₀ = 2,5 мм, кривая 2 и квадратики для R₀ = 3 мм)

тальные и расчетные данные свидетельствуют о достаточно сильной зависимости величины E от рода газа и параметров разряда.

Для определения границ режимов дугового разряда рассчитывался энергетический баланс разряда в локальных и интегральных величинах. В первом случае сравнивалось соотношение удельных мощностей механизмов излучения q_R , теплопроводности q_T и джоулевой диссипации q J в центре разряда. Во втором - определялись суммарные по всему объему разряда мощности лучистых энергопотерь Q_R и джоулева тепловыделения Q_J , а также тепловая мощность Q T , уходящая из разряда за счет механизма теплопроводности через площадь боковой стенки. Следует отметить, что в расчетах с высокой точностью выполнялись балансовые соотношения как интегральные Q J = Q R + Q T , так и локальные q J = q R + q_T во всех расчетных точках. По удельным и интегральным энергетическим характеристикам рассчитывались отношения k_L = q_R/q_J и k I = Q R /Q J , в качестве критериев при определении границ приняты значения к = 0,1, 0,5 и 0,9. При значении k < 0,1 влияние излучения в энергобалансе пренебрежимо мало, при k > 0,9, наоборот, доминируют радиационные энергопотери. Значение k = 0,5 соответствует равенству вкладов теплопроводности и излучения. Из решения уравнений (1)-(4) для указанных значений к определены величины силы тока Г и максимальной температуры в центре разряда T max .

Результаты расчетов для воздуха при атмосферном давлении приведены на рис. 3 и 4. На рис. 3 для значений k = 0,1, 0,5 и 0,9 отображены зависимости I^*(R 0 ) , каждая из которых является геометрическим местом точек, соответствующих режимам с силой тока Г в диапазоне значений R 0 = 5 ÷ 50 мм. Сплошные линии 1, 2 и 3 на рис. 3–10 соответствуют значениям k I = 0,9, 0,5 и 0,1, штриховые линии 4, 5 и 6 относятся к аналогичным значениям k_L . Кривые 2 и 5, для которых выполняются равенства Q R = Q T и q_R = q_T , делят плоскость R 0 - 1 на две области, выше кривых находятся режимы, в энергобалансе которых вклад излучения больше, ниже – режимы с более сильным влиянием теплопроводности. Выше границ 1 и 4 расположены режимы, в энергобалансе которых доминирует излучение Q R >> Q T и q_R >> q_T , соответственно, теплопро-

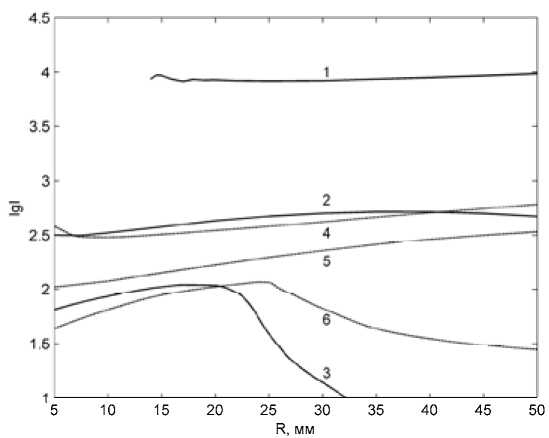
Рис. 3. Зависимости lgI^*(R 0 ) для воздуха при p = 0,1 МПа

R, мм

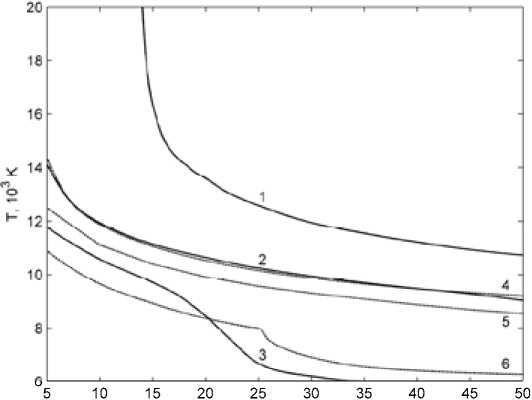
Рис. 4. Зависимости T_max(R₀) для воздуха при p = 0,1 МПа

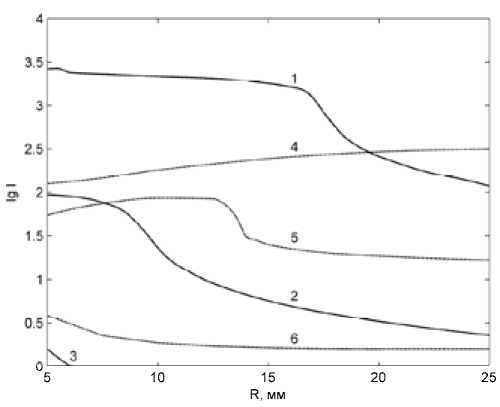
Рис. 5. Зависимости lgI*(R0) для воздуха при p = 1 МПа водные режимы, когда QT >> QR и qT >> qR, находятся ниже кривых 3 и 6. Графики значений максимальной температуры Tmax(R0) в центре разряда, соответствующие полученным зависимостям I*(R0), приведены на рис. 4. Зависимости Tmax(R0) для всех значений k имеют монотонно падающий характер. Явно выраженный излом кривых 6 на рис. 3 и 4 связан с наличием в зависимости X(T) для воздуха локального максимума Xmax = 4,2 Вт/(м*К) при T = 7 кК (при T = 6 кК и 8 кК величина X = 2,4 Вт/(м*К)).

На рис. 5 и 6 приведены зависимости I^*(R 0 ) и T max (R 0 ) для воздуха при давлении p = 1 МПа. Кривые на графиках построены в диапазоне значений R₀ = 5 ÷ 25 мм, при расчете структуры было установлено, что увеличение давления с 0,1 МПа до 1 МПа приводит к уменьшению по-

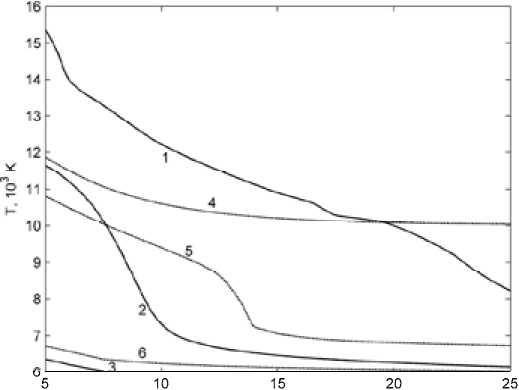
R, мм

Рис. 6. Зависимости T_max(R₀) для воздуха при p = 1 МПа

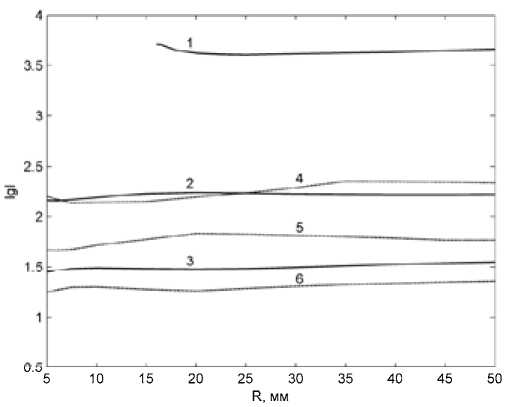
Рис. 7. Зависимости lgI*(R0) для аргона перечного размера разрядного столба примерно в 2 раза. Изменение давления в наибольшей степени влияет на излучательную способность газа, при повышении давления пропорционально растет мощность радиационных энергопотерь, по этой причине переход к радиационному режиму наблюдается при существенно меньших значениях тока и температуры. Изломы на кривых 1 и 5 также являются следствием локальных максимума (Xmax = 3,9 Вт/(м*К) при T = 8 кК) и минимума (Xmin = 1,7 Вт/(м*К) T = 10 кК) в зависимости X(T) для воздуха при давлении p = 1 МПа.

В отличие от молекулярных газов аргон имеет сравнительно невысокую излучательную способность, коэффициент теплопроводности также существенно ниже (особенно для темпе- – 188 –

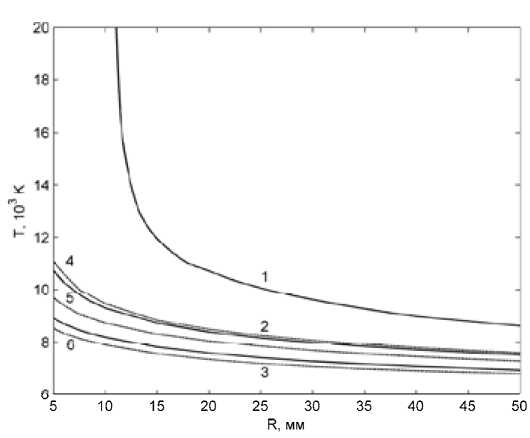
Рис. 8. Зависимости T_max(R 0 ) для аргона

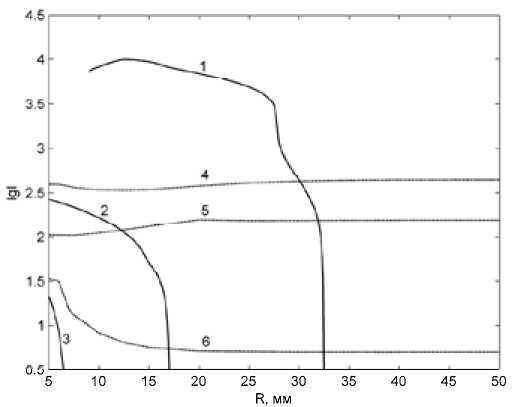
Рис. 9. Зависимости lgI (R0) для углекислого газа ратур T < 10 кК) и зависимость Х(T) имеет более ровный характер. Границы режимов для аргона при атмосферном давлении приведены на рис. 7 и 8. Отличительной особенностью графиков (за исключением кривой 1 на рис. 8) является достаточно слабая зависимость от радиуса.

Для углекислого газа следует отметить близкую с воздухом по характеру и значениям зависимость Х( T) и существенно более высокие значения коэффициента черноты, коэффициент электропроводности у СО₂ выше при температурах T <  11 кК, далее соотношение становится обратным. Зависимости Г (R₀) и T_max(R₀) для углекислого газа при давлении p = 0,1 МПа отображены на рис. 9 и 10. К особенностям интегрального энергобаланса для СО₂ можно отнести то, что значениям R 0 > 32 мм соответствуют только радиационные режимы.

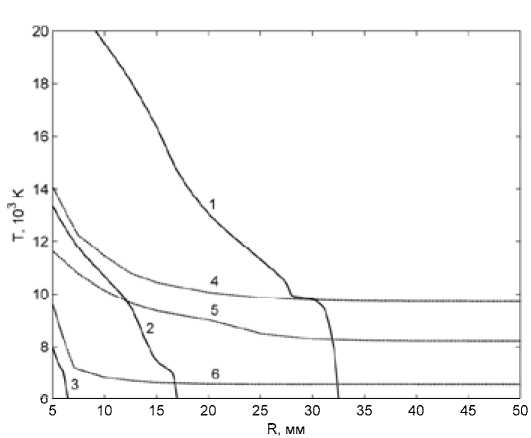
Рис. 10. Зависимости T_max(R₀) для углекислого газа

Заключение

Таким образом, рассчитанные зависимости дают возможность оценивать степень влияния энергетических механизмов и величину максимальной температуры в дуговом разряде при различных условиях. В статье приведены два варианта расчета границ радиационного и теплопроводного режимов: в удельных и интегральных величинах. Сложно однозначно определить, какой из них является более предпочтительным для анализа энергобаланса. С одной стороны, соотношение интегральных мощностей наиболее полно отражает энергобаланс всего разряда в целом. С другой – именно соотношение удельной мощности энергетических механизмов в центре разряда устанавливает масштаб температуры, от которого в значительной степени зависят многие, в том числе и интегральные характеристики разряда. По-видимому, в каждом конкретном случае при анализе энергетического баланса следует исходить из цели исследования и специфики поставленной задачи.