Расчет характеристик незамкнутого осевого гидростатического подшипника с учетом шероховатости опорных поверхностей

Качество конечного изделия зависит от качества проектирования, в частности, от точности и достоверности расчетов основных параметров изделия. Особенно это актуально при проектировании гидростати- ческих опор (подшипников и направляющих). Традиционные методики расчета гидростатических опор основаны на использовании в качестве исходных параметров их номинальных значений. Однако откло- нения этих параметров бывают соизмеримы с толщиной несущего слоя смазки, разделяющего опорные поверхности гидростатической опоры, и существенно влияют на выходные характеристики [1–3]. В работе [4] рассмотрено влияние круговой шероховатости поверхностей незамкнутого осевого гидростатического подшипника (ГСП) на характеристики слоя смазки. Данные результаты приемлемы для питания гидростатической опоры смазкой по схеме «насос-карман». Однако в большинстве случаев ГСП работают с дросселями постоянного сопротивления либо с регуляторами расхода смазки.

В данной работе на примере незамкнутого осевого ГСП с центральной несущей камерой при дроссельной компенсации расхода смазки (рис. 1) исследовано влияние круговой шероховатости опорной поверхности на характеристики подшипника. Входное сопротивление дросселя R др при этом изначально рассчитывается по номинальному значениям параметров подшипника.

При нагнетании давления p н в подшипник подвижная часть 2 поднимается на величину толщины несущего слоя h ₀. Сопротивление дросселя R _др как правило рассчитывается исходя из условия Р _к0 / р н = 0,5. Здесь P _к0 - давление в несущей камере, соответствующее расчетной толщине слоя h 0 при гладких опорных поверхностях, P н – давление нагнетания смазки.

С учетом шероховатости усредненная толщина несущего слоя будет иметь вид h = h0 + 0,5Rz(1 - sin x),               (1)

2 n- m ( r - r )

где x =------------, здесь m = (rn - rK)/ Sm - количе- r — r пк ство волн шероховатости на опорной перемычке подшипника; Sm – средний шаг шероховатости; Rz – высота шероховатости.

Для большей общности результатов и для сокращения вычислений сравнительное исследование про-

водили в безразмерной форме. В математической модели размерные величины заменяли безразмерными: P i = p i / p _н - безразмерный параметр давления; H i = h i / h 0 - безразмерный параметр толщены несущего слоя; R i = r i / r_n - безразмерный параметр радиальных размеров; RZ = Rz/ h ₀- безразмерный параметр высоты шероховатости; W = w /( п - r „ ² - p_H )-безразмерный параметр несущей способности; Q = q - ц /( n- h 0 - p_H ) - безразмерный параметр расхода смазки.

Для дальнейших исследований использовали основные характеристики слоя смазки, полученные в [4]:

– толщинау несущего слоя смазки:

H i = 1 + 0,5 - RZ - I 1 - sin -

2 n- m ( R i - R _к) i - R K .

– расход смазки в слое подшипника

Q = -hX

- 3 P k + 4 P - P 2 A R

– несущую способность гидростатического подшипника, полученную решением с использованием численного метода Симпсона:

W = P_K - R _K2 + 1— R L _x кк 3 n

x[ P k + P n + 2 ( P 2 + P 4 + ... + P n - 2 ) + 4( P 1 + P 3 + ... + P n - 1 )] ,

– уравнение Рейнольдса в конечно-разностном виде:

+ R i

H i

H i

P i + 1

2 A R

P i + 1 - 2 P i + P i - 1 A R ²

+ 3 H i

P i + 1 - P - 1

2 A R

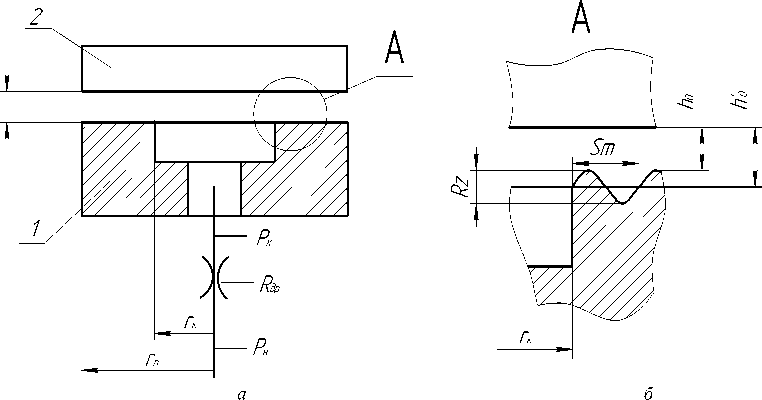
Рис. 1. Гидростатический подшипник: а – схема подшипника; б – форма опорной поверхности

Особенность решения данной задачи заключается в том, что в гидростатическом подшипнике давление в несущем кармане зависит от величины и направления внешней нагрузки. Текущее значение давления в несущем кармане определяется балансом расходов смазки через слой гидростатического подшипника и через дроссель постоянного сопротивления: Q _др= Q _п.

Расход через дроссель равен

Решив (9) совместно с (5) для 1-й точки, определим формулы для нахождения первых прогоночных коэффициентов F 1 , и V 1 :

F = b 2 ■ ^c 1 ^{- b} 1 ■ c 2

^a 1 ■ c 2 ^{- a} 2 ■ ^c 1 ’

c 2 ■ ^d 1

^a 1 ■ c 2 ^{- a} 2 ■ ^c 1

Q др

1 - Р к

R др ,

где а1 =-3Ащ + ^; b1 = 4Ащ ; C1 =-Ащ ; d1 = ;

R др                             R др

R ■ H H 3 ■ H' ■ R ,    2 R ■ H аг = —i-----; Ьг =--1-;

²   A R ² 2 A R    2 A R     ²     A R ²

(1 - Рк 0) ■ ln R где R =-----0------ - сопротивление дросселя,

H 03 ■ Р .0

которое рассчитывается при проектировании гидростатического подшипника и определяется номинальными параметрами опоры.

Решение системы (5) будет иметь вид

P i - 1 = F i P i + V i ,                  (7)

где F i +1 , V i +1 – рекуррентные формулы для вычисления прогоночных коэффициентов; здесь

F ,=       V ,= BVL.

i 1 - BFi i1 - BFi где

A =f—₊ 3(H i + 1 - H i - 1 ) ₊ 1 1

( 4 Ri        8 Hi2 v    3(Hi+1 - Hi-1)11

B =

( 4 Ri       8 Hi2

Учитывая выражения (3) и (6), получим

1 - P . , ,

~--= ^А щ ■ ^{( - 3} ■ ^Р к ^{+ 4} ■ ^P 1 - ^P 2 ) ,

R _др

Л    H 33 ■ R_x

где A^ = — 1

2 ■A R

.

R i ■ H\	H 3 ■ H ■ R
C2 = —  1 A R 2	■ + — +----1---1 2 A R    2 A R

Воспользовавшись вторым граничным условием ( P\_R = 1 = 0) и известными прогоночными коэффициентами F _i , V _i , обратным ходом при i = n , n –1, …, 2, 1 найдем недостающие неизвестные значения функции P n –1 , P n –2 , … , P 1 .

Зная функцию распределения давлений P i в несущем слое смазки рассматриваемого подшипника, определили несущую способность (4) и расход смазки (3).

Дальнейшее исследование проводили с использованием программной реализации, составленной на языке Object Pascal в среде Delphi.

Для корректного сравнения полученных результатов несущей способности и расхода смазки при различной шероховатости и установления рекомендаций по допустимой шероховатости была определена относительная погрешность расчетов, равная 10–6.

На величину и форму распределения давления в большей степени влияет количество шагов шероховатости. Это объясняется тем, что чем больше количество шагов шероховатости в пределах граничных условий (от P к до 0), тем меньше перепад давления на каждом шаге (рис. 2). Однако величина шероховатости приводит к снижению давления в несущей камере, а это в свое время приведет к снижению несущей способности подшипника.

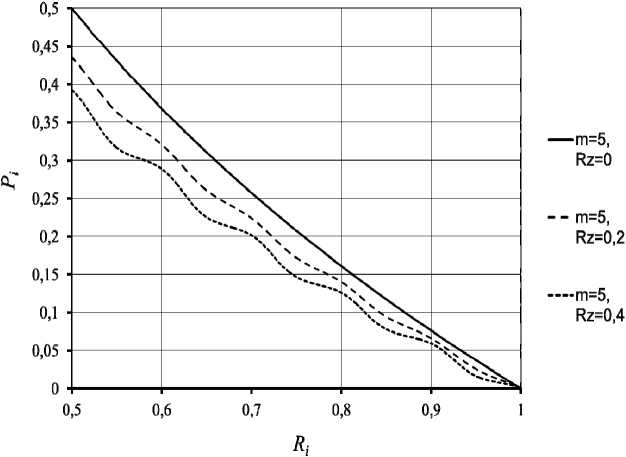
Рис. 2. Графики распределения давления по ширине опорной перемычки

а                                        б

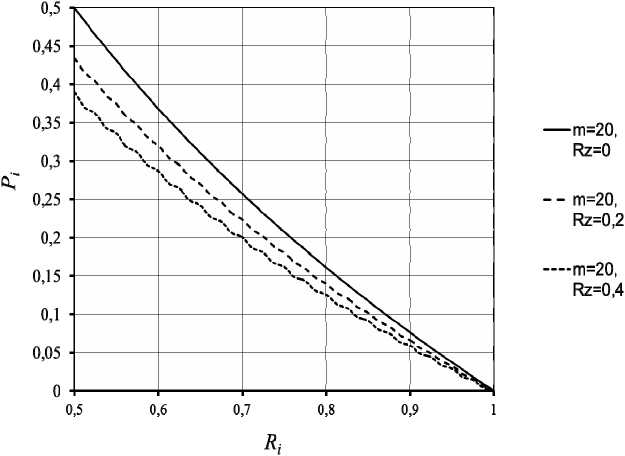
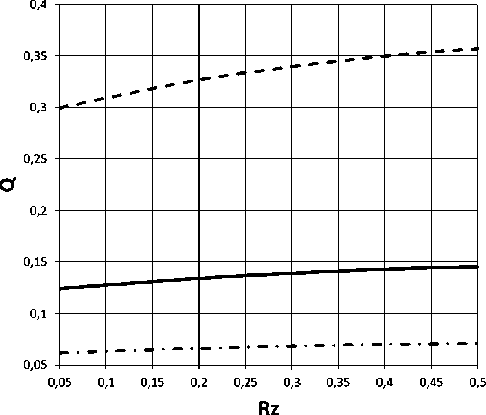
Рис. 3. Влияние шероховатости поверхности на несущую способность ( а ); расход смазки ( б )

б

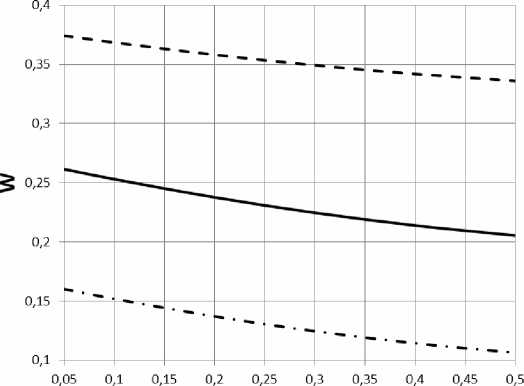
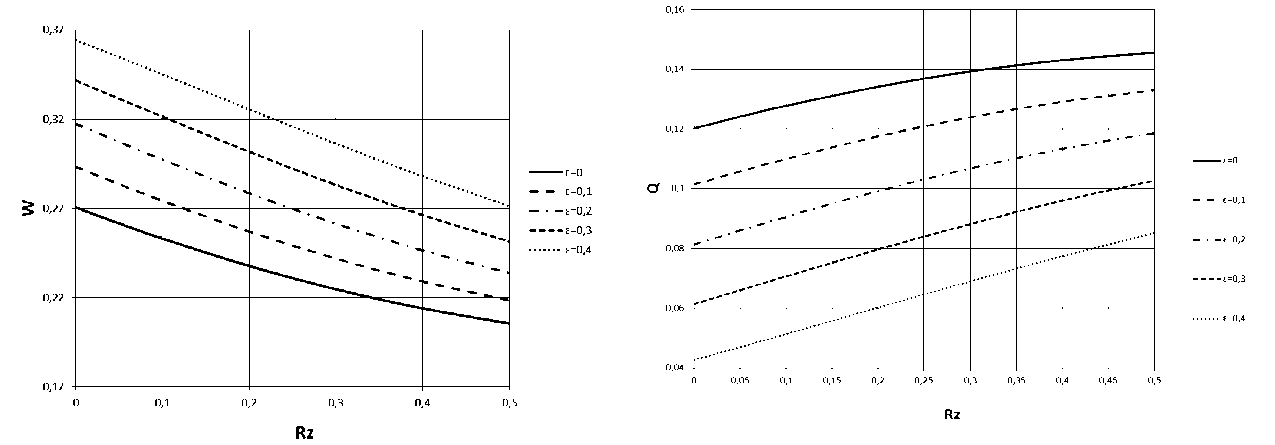
Рис. 4. Влияние шероховатости поверхности на нагрузочные ( а ) и расходные ( б ) характеристики подшипника

Расчеты показывают, что при величине шероховатости, равной половине толщины несущего слоя (при h ₀ = 20 мкм значение шероховатости составит Ra = 0,25), несущая способность может отличаться от расчетного значения на 10–13 % в подшипниках с узкими перемычками ( R 1 ≥ 0,75) и на 35–40 % в подшипнике с широкими перемычками ( R 1 ≥ 0,25). Расход смазки при этом увеличивается (рис. 3).

При воздействии на подвижную часть подшипника нагрузки действительная величина зазора изменяется на величину ε :

Н 0 = 1 – ε, (11) где ε – смещение подвижной части подшипника под действием нагрузки.

В нагруженных подшипниках влияние шероховатости на нагрузочные и расходные характеристики подшипника аналогично не нагруженным подшипникам (рис. 4).

Полученные зависимости позволяют проводить корректировку несущей способности и расхода смазки в зависимости от шероховатости опорных поверхностей на стадии проектирования гидростатических подшипников.