Расчет характеристик пирамидального перехода ТЕМ-камеры

Для проведения испытаний электронных компонентов и систем на электромагнитную совместимость при воздействии на них электромагнитных полей большой амплитуды используются ТЕМ-камеры [1], состоящие из регулярной части и двух пирамидальных переходов (рис. 1).

Регулярная часть ТЕМ-камеры представляет собой полосковую линию передачи с центральным проводником 1 и наружным экраном прямоугольного сечения 2 . Для согласования геометрических размеров регулярной части ТЕМ-камеры с разъемами генератора и нагрузки 3 на ее входе и выходе включены согласующие пирамидальные переходы 4 , обеспечивающие постоянство волнового сопротивления по всей длине ТЕМ-камеры.

Объект испытаний 5 помещается в середину регулярной части ТЕМ-камеры, где электромагнитное поле имеет минимальную неравномерность и не содержит продольных составляющих. Генератор, пирамидальные переходы 4 и согласованная нагрузка обес- печивают в регулярной части ТЕМ-камеры режим бегущей волны, которая имитирует электромагнитную волну в открытом пространстве.

Требование высокой однородности поля в месте расположения испытуемого объекта при его больших габаритах вынуждает применять ТЕМ-камеры с большими размерами поперечного сечения регулярной части. Однако при больших поперечных размерах ТЕМ-камеры в ее регулярной части на некоторых частотах могут распространяться кроме основного и высшие типы волн [2], которые могут стать причиной возникновения резонансных явлений в ТЕМ-камере [3]. В этом случае равномерность поля в регулярной части в месте расположения испытуемого объекта нарушается, и результаты проведения испытаний становятся недостоверными.

Целью работы является расчет электрических характеристик пирамидального перехода ТЕМ-камеры. Результаты расчета электрических характеристик актуальны для исследования частотных параметров

Рис. 1. Конструкция ТЕМ-камеры

ТЕМ-камеры, установленной в Дирекции по техническому развитию ОАО “АВТОВАЗ”, имеющей габариты 18 х 8 х 27 м ³ и предназначенной для проведения испытаний транспортных средств на электромагнитную совместимость на частотах свыше 10 КГц.

Для расчета электрических характеристик нерегулярных линий передач применялся метод с использованием многомодовых матриц рассеяния [4]. В соответствии с этим методом пирамидальный переход, который является нерегулярной линией передачи, представлялся в виде каскадного соединения регулярных отрезков линии передачи и неоднородностей в виде скачков геометрических размеров поперечного сечения линии передачи.

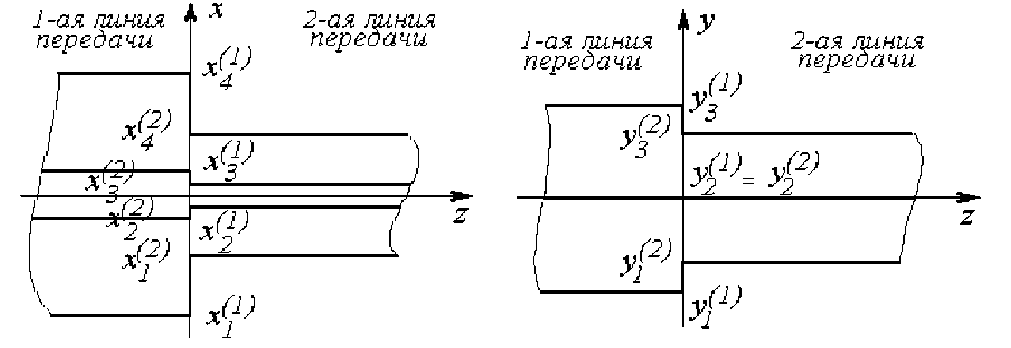
Расчет многомодовой матрицы рассеяния неоднородности в виде скачка параметров линии передачи Рассмотрим неоднородность в полосковой линии передачи в виде скачка геометрических размеров (рис. 2).

При падении электромагнитной волны на неоднородность вблизи нее возбуждается весь спектр собственных волн линии передачи, по которым можно определить многомодовую матрицу рассеяния.

В [5] описан метод расчета многомодовой матрицы рассеяния неоднородности в виде скачка геометрических размеров в полосковой линии на основе строгого решения задачи дифракции электромагнитной волны методом частичных областей. В соответствии с этим методом рассмотрим две линии пере- дачи 1 и 2 с разными геометрическими размерами и электродинамическими параметрами заполняющих сред (рис. 2).

При падении на неоднородность слева электромагнитную волну в 1-ой линии передачи можно представить в виде суперпозиции ее собственных N волн.

N

E = L A n " e 1n ^(x,y) • e^XP⁽ - i Y ln z),

n = 1

. N _

H = L A n " ^h 1n ^(x,y) • e^XP⁽ - i Y ln z).

n = 1

где A _n , Y 1 _n , e 1 _n , h_{1 n} — соответственно комплексная амплитуда, продольное волновое число и составляющие электрического и магнитного полей n -го собственного типа волны в 1-ой линии передачи.

Такая волна на неоднородности частично отражается и частично проходит во вторую линию передачи. Выражения для сост а вляющих полей в первой линии передачи E ₁ , H ₁ можно записать в виде суперпозиции падающих и отраженных волн, а во второй линии передачи – в виде прошедших волн E ₂ , H ₂ .

Nw

*                 *•

E l = L A n e in ^(x-y) ■ ^exP( ^- i Y ln z) + L B n e in (^x-y) • ^exP⁽i Y ln z).

n=ln

Nw

***

Hl = L AnhlnCx.y) ■ eXP( — iYlnz) — LBnhln (X,y) ■ eXP( iYlnz). n=ln

E 2

w

*

= L Cne2n(X,y) ^ eXP( — iYlnz), n=l

w

*          *

^H 2 = L C n h 2n (^X,y⁾ • ^eXP⁽ — i Y ln z). n = l

- б -

- а -

Рис. 2. Скачок геометрических размеров в полосковой линии передачи

В этих выражениях B _n , C _n - комплексные амплитуды соответственно отраженных и прошедших n -ых собственных типов волн в 1-ой и 2-ой линиях передачи.

В плоскости скачка параметров линии передачи при z = 0 должны выполняться гра-

X b kn = § kn - E b ni c ki ,

c kn

i = 1

X

= 5 kn ⁺ E b ik c in ,

ничные условия для составляющих электри-

ческого и магнитного полей, касательных

^δ kn

i = 1

d kn = ² ‘ ^C kn .

– единичная дельта-функция,

плоскости скачка

——         ——

E 1 т = E 2 т при

——

^H 1 т = H 2 т при

< x е ^[ x^y ,x 4 ²⁾ ] , ' У е [ У^У ² ] , _< x е ^[ x⁽₁¹⁾ .x^ ^] , _ У ^{е [} У? .У^{( 1 ]} ,

8 kn =

' 1

при k ^ n при k = n , k = 1,2,3,'"’X,

——

E 1 т = E 2т = 0 при

b _nk

c nk

*

1 _Г -               -                —

= —J e l n ^{( x} , У ) h 2 k ^{( x} , У ) 1 z dS , N

2 k

S 1

*

1 Г            *           —

_V J e 1 n ⁽ x , У ) h 2 k ⁽ x , У ) ¹ z d^S , N

1 k S ₂

*

k^LIV ²) V ¹)]    k (^i;

x ^е [ x i ,x i J ^ [ x ,x 4 J ,^y   L ^y 1 ,^y 3 J ,

(2)   (2)             (2)   (1)       (1)   (2)     (5)

L ^{x е} L x i ,x 4 J , ^y = L ^y 3 ,^y 3 J^ У ,^y i J •

N jn

= J e jn ⁽ x , У ) h — jk ⁽ x , У ) — z ^dS S , L                           _

, j = 1,2 .

Подставляя соотношения (1), (2) в (3), (4), получим систему уравнений для касательных составляющих полей

NXX

E A nein(x,y) + E BneU(x,y) = E Cn^2n(x,y)’ n=1                       n=1n

N                 x                 x

~—                           ~—                            ~—x^

^A n h 1n ^(x,y) - E ^B n h 1n ^(x,y) = E ^C n h 2n ^(x,y)^V

_ n=1                       n=1n

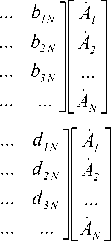
Применяя условие ортогональности собственных типов волн к уравнениям системы (6) и используя граничное условие (5), получим систему линейных алгебраических уравнений, связывающую амплитуды отраженных ( B ₁, B ₂,..., B _n ,...) и прошедших ( C ₁, C ₂,..., C _n ,...) волн с падающими ( A ₁, A ₂ ,..., A _N ), которую в матричной форме

можно записать в виде

a11   a12

a21   a22

a31   a23

c 11    c 12    c 13

c 21    c 22    c 23

c 31    c 23    c 33

" в 1 B ^ 2 B 3

_ ■■■

C 1 C2 C 3

b 1 b₂ b

...

d1 d d

...

'22

d1 d d b1 b2 b

...

...

, (7)

, (8)

Система уравнений (7) и (8) связывает амплитуды N собственных типов волн в 1ой линии передачи A ₁, A ₂,..., A _N , падающих на неоднородность, с бесконечным числом собственных типов волн, отраженных от неоднородности с амплитудами B ₁, B ₂, B ₃,..., и прошедших во вторую линию передачи волн с амплитудами C ₁, C ₂ , C ₃ ,....

При этом амплитуды собственных типов волн A ₁, A ₂,..., A _N , падающих на неоднородность, считаются заданными, а амплитуды отраженных B ₁, B ₂ , B ₃ ,... и прошедших C ₁, C ₂, C ₃,... волн – неизвестными.

Бесконечную систему линейных алгебраических уравнений (7) и (8) можно решить методом редукции. Из решения этой системы уравнений можно найти элементы многомодовой матрицы рассеяния [4]. Для вычисления j -го столбца многомодовой матрицы рассеяния в соотношения (7) и (8) следует подставлять следующие значения

амплитуд волн, падающих на неоднородность: A j = 1, A l = 0, l = 1 , 2 ,..., x , l ^ j .

Элементы матрицы рассеяния будут оп-

ределяться отношением амплитуд отраженной B _i и прошедшей C _i волн к амплитуде падающей волны A _j

( ij )

S 11 =

где                    « akn = 5kn +E bnicki ,            (9)

i = 1

B i

A _j

S (ij ) = ^C i

21 A _j

где i = 1,2,..., x , j = 1,2,...,N .

Применяя эту процедуру для значе-

ний j = 1,2,...,N , можно найти элементы матрицы рассеяния S ₁ ⁽ ₁ ^{ij )} , S ₂ ⁽ ₁ ^{ij )} .

Для определения элементов многомодовой матрицы рассеяния S ₁ ⁽ ₂ ^{ij )} , S ₂ ⁽ ₂ ^{ij )} необходимо решить аналогичную изложенной выше задачу о возбуждении волн неоднородностью для случая, когда волна на нее падает справа.

Результаты расчета многомодовой матрицы рассеяния неоднородности в виде скачка геометрических размеров в полосковой линии Ниже в качестве примера приведены результаты расчета многомодовой матрицы рассеяния для неоднородности в виде скачка геометрических размеров в полосковой линии (рис. 2) с параметрами х^ = -Х;1) = 9000мм, х31) = - х21) = 5 600 мм, у^ = у 22) = 0, у31) =-у<1 = 4 000 мм, х42) = -х(2) = 8 500 мм, х(32) = -х(22) = 5150 мм, у<2 =-yW = 3 750 мм , ^ 1 = ^2 = 1 , ^1 = ^2 = 1 .

При таких геометрических размерах линий передач в них на частотах менее 7 МГц распространяющимся является только один собственный тип волны, на частотах менее 30 МГц – 7 собственных типов волн [2].

При суммировании рядов в соотношениях (9) – (11) число членов ряда ограничивалось условием, что дальнейшее увеличение числа членов ряда не изменяло все элементы матрицы рассеяния на величину, превышающую значение 0,0001.

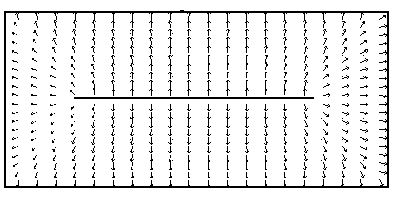
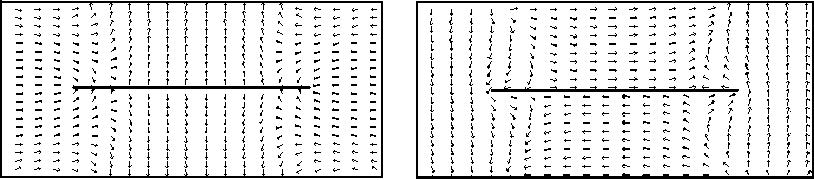
Из анализа рассчитанных матриц рассеяния следует, что с наибольшей амплитудой основной тип волны в линии передачи возбуждает пятый тип волны. Это обусловлено тем, что структура поля пятого типа волны в наибольшей степени подобна структуре основного типа волны [6]. На рис.3 приведены структуры электрического (а, в) и магнитного (б, г) полей первого (а, б) и пятого (в, г) собственных типов волн линии передачи.

Из представленных структур полей видно, что в центральной области линии передачи направления силовых линий электрического и магнитного полей совпадают.

При изменении частоты и геометрических размеров линий передачи значения элементов многомодовой матрицы рассеяния изменяются. На рис. 4 приведены частотные зависимости элементов матрицы рассеяния.

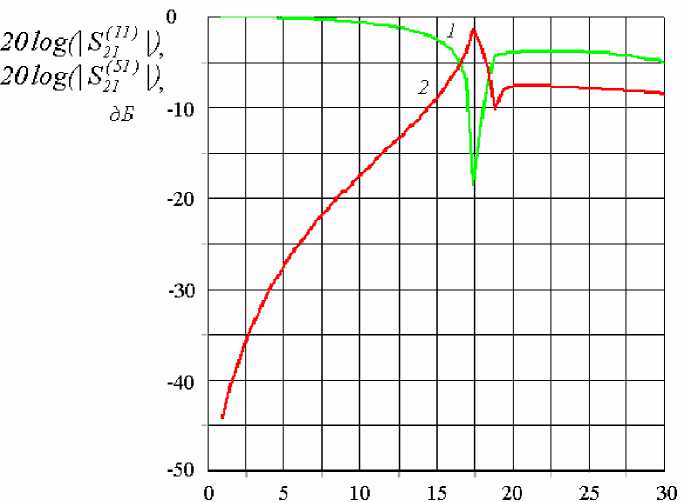
Из представленных частотных зависимостей модулей элементов матрицы рассеяния следует, что в диапазоне частот до 17,5 МГц модуль коэффициента передачи для основного типа волны S ₂ ⁽ ₁ ¹¹⁾ монотонно уменьшается. На частоте 17,5 МГц возникают условия распространения для 5-го собственного типа

- а -

- б -

- в -                                                    - г -

Рис. 3. Структуры электрического (а, в) и магнитного (б, г) полей первого (а, б) и пятого (в, г) собственных типов волн

X МГу.

Рис. 4. Частотные зависимости элементов матрицы рассеяния

20log(| S ₂ ⁽ ₁ ¹¹⁾ |) (кривая 1) и 20log(| S ₂ ⁽ ₁ ⁵¹⁾ |) (кривая 2)

волны, имеющего большую амплитуду, и на графике зависимости коэффициента передачи для основного типа волны S ₂ ⁽ ₁ ¹¹⁾ появляются изломы. Возбуждающиеся на других частотах остальные собственные типы волн на частотную зависимость коэффициента передачи по основной моде S ₂ ⁽ ₁ ¹¹⁾ не влияют из-за их малой амплитуды.

Результаты расчета пирамидального перехода для ТЕМ-камеры

С использованием полученных численных результатов расчета многомодовых матриц рассеяния неоднородностей в виде скачков геометрических размеров полосковой линии и выражения для матрицы рассеяния регулярных отрезков линии передачи [4] были рассчитаны частотные зависимости элементов матрицы рассеяния пирамидального перехода, изображенного на рис. 5 и имеющего геометрические размеры x41 = -х(1 = 9000 мм, x^ = -x21) = 5600 мм, yV* = -y((1) = 4000 мм, x^ = -x((2) = 490 мм, x(32) = -x22) = 350 мм, y22> =-y!2) = 292 мм, z0 = 10360 мм .

Для этого использовался метод расчета нерегулярных линий передачи на основе многомодовой матрицы рассеяния [4]. Переход моделировался N регулярными линиями одинаковой длины и N + 1 неоднородностями в виде скачков геометрических размеров.

Для определения необходимого числа регулярных линий N , аппроксимирующих пирамидальный переход, рассчитывались модули элементов многомодовой матрицы рассеяния S ₁ ⁽ ₁ ¹¹⁾ , S ₁ ⁽ ₁ ⁵¹⁾ на частотах 5 МГц и 20 МГц , при которых в участке пирамидального перехода с наибольшими геометрическими размерами обеспечивались соответственно одномодовый и многомодовый режимы.

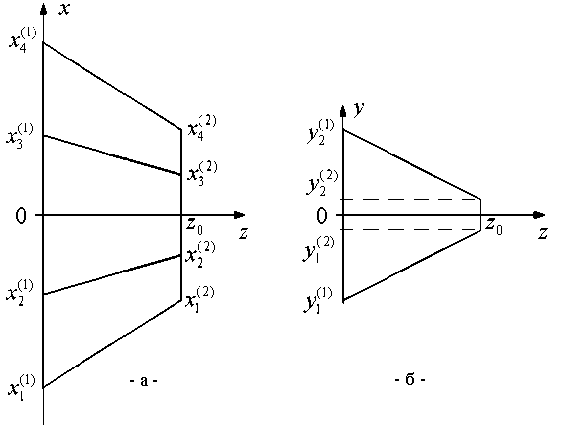
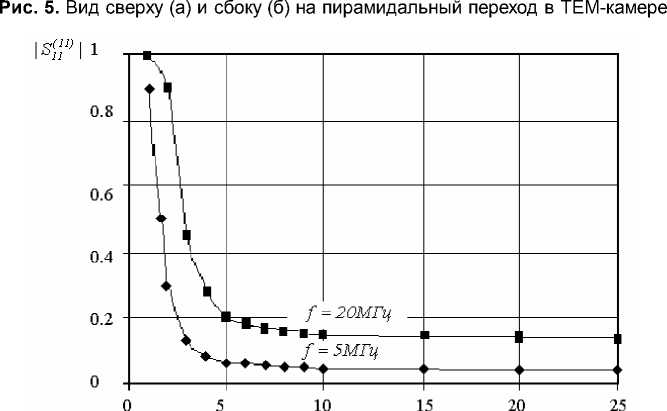
На рис. 6 представлены рассчитанные зависимости модулей коэффициента отражения _{S 1}(₁11) _{и S1}(₁51) от числа регулярных отрезков N .

Из представленных результатов следует, что увеличение числа регулярных отрезков N свыше 10 мало влияет на элементы многомодовой матрицы рассеяния. Аналогичные зависимости от числа разбиений имеют и другие модули элементов многомодовой матрицы рассеяния. С наибольшей амплитудой основной первый тип волны возбуждает в пирамидальном переходе 5-ый собственный тип волны.

N

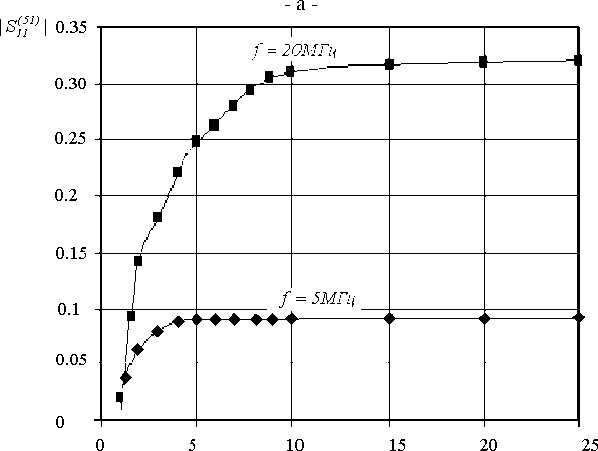
- б -

N

Рис. 6. Зависимость модулей элементов многомодовой матрицы рассеяния | S1(111) | и | S1(151) | от числа регулярных отрезков N

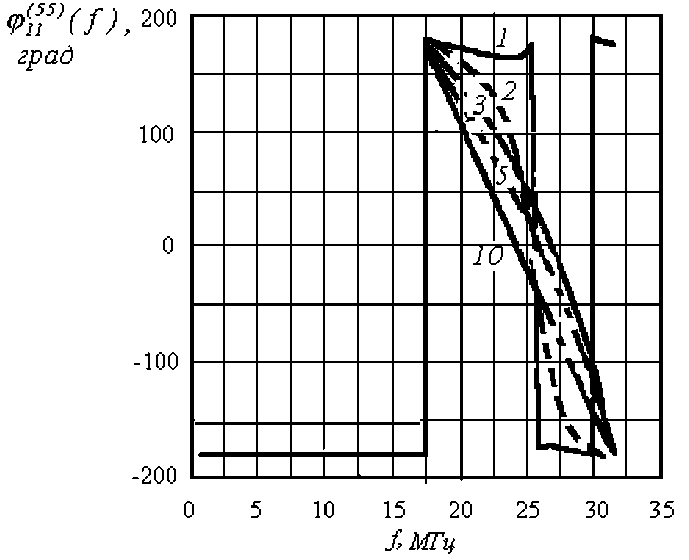
Рис. 7. Частотная зависимость фазы коэффициента отражения 5-го типа волны ϕ ₁ ⁽ ₁ ⁵⁵⁾ ( f ) .

Цифры у кривых – число регулярных отрезков линий передач N

Частотная зависимость фазы коэффициента отражения для пятого типа волны ϕ ₁ ⁽ ₁ ⁵⁵⁾ при различном числе разбиений N представлена на рис. 7.

Из представленных зависимостей видно, что в диапазоне частот 5-17.5 МГц фаза коэффициента отражения 5-го высшего типа волны постоянна и равна _- 180 ⁰ . Это обусловлено тем, что анализируемая структура в этом диапазоне частот не допускает распространение данного типа волны. По мере увеличения частоты свыше 17.5 МГц в пирамидальном переходе критическое сечение [8], которое разделяет область с распространяющимися и затухающими волнами, смещается внутрь перехода, и вносимый фазовый сдвиг изменяется.

Закон изменения фазового сдвига от частоты также зависит от числа разбиений N . По мере увеличения числа разбиений частотная зависимость фазы коэффициента отражения стабилизируется, и при увеличении числа разбиений N свыше 10 не приводит к изменению частотной зависимости фазы коэффициента отражения 5-го собственного типа волны.

Заключение

Рассчитана и проанализирована многомодовая матрица рассеяния пирамидального перехода ТЕМ-камеры. Определены условия, обеспечивающие заданную точность вычисления элементов многомодовой матрицы рассеяния. Полученные результаты использованы для расчета частотной характеристики ТЕМ-камеры [7].

Работа выполнена при финансовой поддержке Российско-американской программы “Фундаментальные исследования и высшее образование” (“BRHE”, CRDF Project RUX0-014-SA-06) и Российского фонда фундаментальных исследований (гранты №№ 07-07-97601-р_офи, 06-07-08074-офи).