Расчет характеристик теплообмена оребренной стенки

Введение. Система терморегулирования (СТР) космических аппаратов выполняет важнейшую функцию по обеспечению оптимальных температурных режимов всех блоков и узлов в реальных условиях эксплуатации [1–5]. В СТР для интенсификации теплопередачи и уменьшения габаритов в теплообменниках широко используются оребренные поверхности, которые находятся в контакте с жидким или газообразным теплоносителем. Характеристики СТР зависят от параметров оребренных поверхностей и теплофизических свойств теплоносителя, поэтому разработка СТР требует решения ряда задач, таких как определение локального коэффициента теплоотдачи на поверхности контакта стенки и теплоносителя, расчет характеристик теплопередачи оребренной стенки и оптимизация ее параметров.

Характеристики теплопередачи рассчитываются по температурному полю в объеме оребренной стенки, полученному из решения задачи теплопроводности. При решении задачи теплопроводности, как правило, делаются различные упрощающие допущения: пренебрегают температурными градиентами по толщине ребра (приближение тонкого ребра), принимают однородное распределение температуры в основании оребренной стенки, задают постоянную величину коэффициента теплоотдачи по оребренной поверхности и др. [6]. Чтобы такие упрощающие допущения не приводили к существенным погрешностям вычислений, необходима проверка правомерности их применения для каждой задачи.

Характеристики процесса теплообмена оребренной стенки и теплоносителя зависят, с одной стороны, от коэффициента теплоотдачи теплоносителя на поверхности теплообменника, с другой стороны, от условий теплопередачи в объеме стенки механизмом теплопроводности. В настоящей работе представлены результаты расчетов характеристик теплопередачи стенки, основанные на определении зависимости коэффициента теплоотдачи теплоносителя ЛЗ-ТК-2 от температуры оребренной поверхности, и моделирования процесса теплопередачи в ребристом теплообменнике с помощью численного решения двумерного уравнения теплопроводности без использования указанных выше упрощающих допущений.

Коэффициент теплоотдачи теплоносителя ЛЗ-ТК-2. По требованиям работы СТР, теплоноситель должен иметь температуру замерзания не выше –80 °С, коррозионную инертность к материалам СТР, пожаробезопасность и обладать рядом других специфических свойств [7; 8]. В качестве рабочего вещества для контура рассмотрим теплоноситель ЛЗ-ТК-2, основой которого является изооктан, имеющий температуру замерзания –107 °С и включающий в себя противоизносные присадки для снижения износа подшипников электронасосных агрегатов. Описание и температурные зависимости физических свойств теплоносителя ЛЗ-ТК-2 приведены в [8].

Расчет коэффициента теплоотдачи проводился с учетом режима движения и физических свойств теплоносителя, геометрических параметров оребренной поверхности. В зависимости от значения числа Рейнольдса Re = uD /ν различают устойчивый ламинарный (Re < 2·10³), переходной (2·10³< Re < 10⁴) и развитый турбулентный (Re > 10⁴) режимы, здесь u – скорость движения теплоносителя, ν – коэффициент кинематической вязкости. Для канала прямоугольного сечения, имеющего высоту a и ширину b , в качестве характерного размера обычно используется величина эквивалентного гидравлического диаметра D = 2 ab /( a + b ). Величина локального коэффициента теплоотдачи α на границе «теплоноситель – оребренная поверхность» определялась с помощью критериальных уравнений, которые базируются на результатах опытных исследований и теории подобия [9]. Для развитого турбулентного режима использовано уравнение, определяющее значение числа Нуссельта,

Nu = 0.021Re °'8 Pr_h ⁰'⁴³ (Pr h / Pr_s) °^.25 f .

Число Прандтля Pr = ν с ρ/λ определяется по значениям коэффициента кинематической вязкости ν, теплоемкости с , плотности ρ и коэффициента теплопроводности λ, соответствующим средней температуре теплоносителя (Pr h ) и температуре поверхности стенки (Pr s ). При длине канала более 50 D значение коэффициента ε = 1. По величине числа Нуссельта рассчитывается значение локального коэффициента теплоотдачи ЛЗ-ТК-2 по формуле

a =

Nu z

D

Расчеты проведены для a = 2,5 мм, b = 1,3 мм и скорости теплоносителя u = 2,9 м/с, получена величина Re = 1,1·104 при характерном значении ν = 0,45 мм2/с. Полученные зависимости коэффициента теплоотдачи α от температуры поверхности стенки Ts приведены на рис. 1 для значений температуры теплоносителя 20, 40 и 60 °С. Из рис. 1 видно, что величина α растет с увеличением как температуры поверхности стенки, так и температуры теплоносителя. Зависимости α(Ts) являются исходными данными для расчетов температурного поля оребренной стенки.

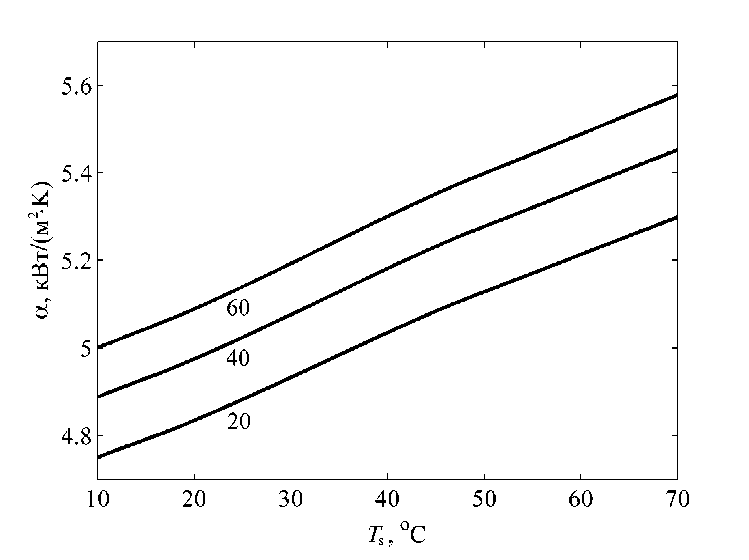
Рис. 1. Зависимости локального коэффициента теплоотдачи ЛЗ-ТК-2 от температуры стенки Fig. 1. Dependence of the local heat transfer coefficient LZ-TK-2 on the wall temperature

Расчет температурного поля в оребренной стенке. Задачей теплового расчета является определение температурного поля и коэффициента теплопередачи, отражающего отношение передаваемой тепловой мощности к разности температур теплоносителя и стенки. Рассмотрим процесс теплообмена теплоносителя ЛЗ-ТК-2 с оребренной стенкой, поперечное сечение которой приведено на рис. 2.

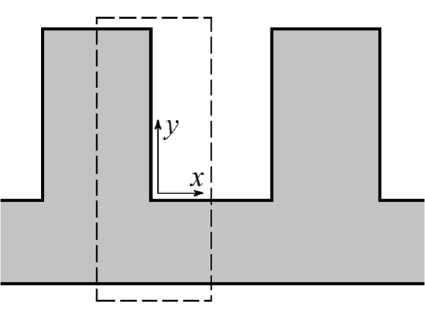
Рис. 2. Схема оребренной стенки и границы расчетной области

Fig. 1. Diagram of the finned wall and the boundary of the calculation area

Расчет температурного поля в стенке теплообменника проводился на основе решения нестационарной задачи теплопроводности. В случае толстого ребра, в котором градиенты температуры сопоставимы по ширине и высоте, численно решается двумерное уравнение теплопроводности вида дТ  3

cp— = Я д

(а ² т   д ² т )

_v д х ²    д '² у

.

Расчетная область задачи, которая представляет собой половину периодически повторяющегося фрагмента оребренной стенки, выделена на рис. 2 штриховым контуром. На внутренних границах стенки задаются условия симметрии по тепловому потоку ∂ q /∂ x = 0, а на поверхностях контакта с теплоносителем (включая торцевую поверхность ребра) – граничные условия третьего рода

1 дТ . т

Я --+ а Т д

= qi=0,L , (2) l=0, L здесь T – температура; x, y – пространственные координаты; l = x, y и L – размер, соответствующий этим координатам; q – плотность теплового потока. При этом полагалось, что температура теплоносителя, контактирующего с оребренной поверхностью, имеет постоянное значение.

Для решения уравнений (1) и (2) применялся метод суммарной аппроксимации с расщеплением задачи по пространственным координатам [10–15]. Температурное поле в объеме стенки Δ T ( x , y ) и с распределение α( T s ) имеет взаимное влияние друг на друга, поскольку α( T s ) определяет величину теплового потока на границе оребренной поверхности с теплоносителем. Согласование этих распределений происходит в процессе получения установившегося решения нестационарной задачи.

В качестве материала стенки рассматривалась сталь 12Х18Н10Т, имеющая коэффициент теплопроводности λ = 19 Вт/(м·К). Температура теплоносителя, контактирующего с верхней оребренной поверхностью, задавалась постоянной и равной 50 °С, на нижней поверхности основания ее значение составляло 60 °С. Значение локального коэффициента теплообмена α определялось в соответствии с величинами температур на поверхности стенки и теплоносителя. На рис. 3 приведено температурное поле для следующих геометрических параметров оребренной стенки: толщина ребра 1,5 мм; высота ребра 2,5 мм; толщина стенки 1,6 мм; расстояние между ребрами b = 1,3 мм. Расчёт проводился для половины периодически повторяющегося фрагмента оребренной стенки, поэтому на рисунке размер основания в направлении x составляет 1,4 мм. Значения температуры на соответствующих изолиниях приведены в градусах Цельсия. В основании стенки градиент температуры наблюдается в направлении y , в направлении x температурные градиенты практически отсутствуют. В ребре градиент температуры есть в обоих направлениях. В данном случае распределения температуры нижних поверхностей основания и ребра близки к однородным, поэтому будет правомерным использование упрощенных расчетных моделей, предполагающих однородность температуры.

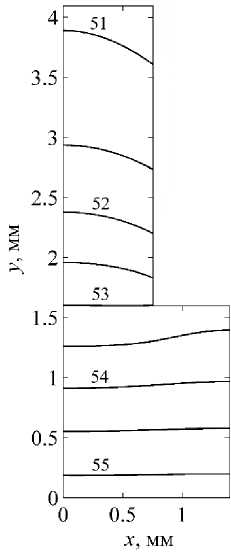
Рис. 3. Температурное поле оребренной стенки при толщинах ребра 1,5 мм и стенки 1,6 мм

Fig. 3. Temperature field of the finned wall at the thickness of the edge 1.5 mm and the wall 1.6 mm

Изменение геометрических параметров отражается на характере температурного поля. На рис. 4 приведены результаты расчета при уменьшении толщин ребра (0,7 мм) и стенки (0,5 мм), при этом высота ребра и ширина основания не менялись. В основании стенки температурное поле существенно неоднородно уже в обоих направлениях, в более тонком ребре увеличение температурного перепада по высоте сопровождается его уменьшением в поперечном направлении.

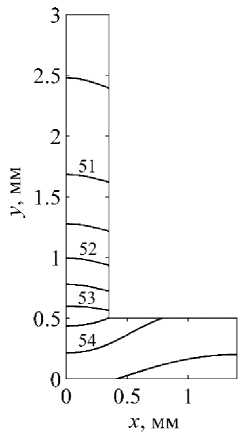
Рис. 4. Температурное поле оребренной стенки при толщинах ребра 0,7 мм и стенки 0,5 мм

Fig. 4. Temperature field of the finned wall at the thickness of the edge 0.7 mm and the wall 0.5 mm

Коэффициент теплопередачи оребренной стенки. Коэффициент теплопередачи k является важной интегральной характеристикой процесса теплообмена оребренной стенки с теплоносителем. Наибольший интерес представляют характеристики теплообмена в объеме стенки и на верхней оребренной поверхности, поэтому величину k определим, как отношение передаваемой тепловой мощности к разности температур теплоносителя T h и нижней гладкой поверхности стенки, а также к площади этой поверхности. Суммарная величина теплового потока, передаваемого стенкой теплоносителю, рассчитывалась на основе решения задачи теплопроводности по распределениям температуры верхней оребренной поверхности T s и локального коэффициента теплоотдачи α по формуле q = α(Расчеты T s – T h ). величины теплового потока проводились в двух модельных приближениях. В первом случае локальный коэффициент теплоотдачи определялся с учетом его зависимостей от T s и T h , которые приведены на рис. 1, во втором – величина α имела постоянное значение, соответствующее температуре поверхности, т. е. задавалась величина α при T s = T h . Сравнение результатов расчетов позволяет оценить погрешность применения упрощенной математической модели, в которой не учитывается неоднородность распределения коэффициента теплоотдачи α по оребренной поверхности.

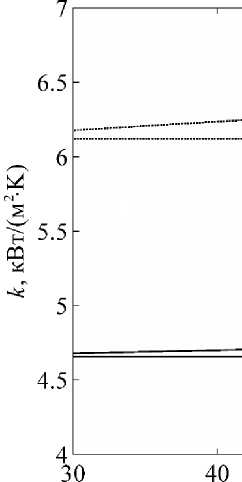
При решении задачи теплопроводности на нижней поверхности основания стенки предполагался идеальный теплоподвод, поэтому здесь температура задавалась с однородным распределением и значением T 0 . В расчетах величина T 0 варьировалась в диапазоне 30–70 °С, температура теплоносителя, контактирующего с верхней оребренной поверхностью, задавалась фиксированной и равной T h = 20°С. На рис. 5 приведены зависимости k ( T 0 ), полученные с помощью обоих рассмотренных модельных приближений. Линии 1 соответствуют конфигурации стенки, приведенной на рис. 3, линии 2 относятся к стенке, приведенной на рис. 4. Горизонтальные прямые получены в результате расчетов с фиксированным локальным коэффициентом теплоотдачи α, что обуславливает постоянство значений k . Растущие графики получены в расчетах с учетом температурной зависимости α( T s , T h ).

60          70

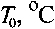
Рис. 5. Зависимости коэффициента теплопередачи от температуры основания стенки Fig. 5. Dependence of the heat transfer coefficient on the wall base temperature

Из расчетов по двум модельным приближениям получены зависимости k ( T 0 ), разность между которыми увеличивается с ростом T 0 (рис. 5). Относительная величина этой разницы приведена на рис. 6. Наибольшее расхождение ожидаемо соответствует конфигурации 2, поскольку в ребре меньшей толщины устанавливаются более высокие перепады температуры, что приводит в итоге к большей неоднородности величины локального коэффициента теплоотдачи α по поверхности ребра. В целом для рассмотренных конфигураций стенки максимальная величина отклонения, которая является погрешностью упрощенной модели, не превышает 5 %. Такая величина погрешности для многих практических расчетов является вполне допустимой, а применение упрощенной модели для рассмотренных конфигураций оребренных стенок оправданным. Однако при других параметрах стенки и свойствах теплоносителя величина расхождения может быть выше, поэтому в каждом случае допустимость применения упрощенной модели требует обоснования и подтверждения путем оценки погрешности расчетов.

Рис. 6. Относительная погрешность расчета коэффициента теплопередачи в упрощенном приближении

Fig. 6. Relative error in calculating the heat transfer coefficient in a simplified approximation

Заключение. Таким образом, в работе проведен анализ процесса теплоопередачи в оребренной стенке теплообменника. На основе критериальных соотношений получены температурные зависимости локального коэффициента теплоотдачи α на оребренной поверхности. Выполнены расчеты температурного поля для двух конфигураций оребренной стенки, оценено влияние геометрических параметров стенки на неоднородность температурного распределения. Получены температурные зависимости коэффициента теплопередачи при использовании двух модельных приближений, отличающихся учетом величины α, определена относительная погрешность упрощенного приближения, не учитывающего температурную зависимость локального коэффициента теплоотдачи.

Acknowledgments. The reported study was funded by Russian Foundation for Basic Research, Government of Krasnoyarsk Territory, Krasnoyarsk Regional Fund of Science, to the research project: “Theoretical and experimental investigation of heat and mass transfer processes in the two-phase system of thermal control” (project № 18-41-242005).