Расчет химических потенциалов компонентов наночастиц

Точное определение химических потенциалов компонентов наночастиц очень важно для нанотехнологий, особенно для изучения роста наночастиц сложного состава. Для расчета химического потенциала обычно применяется метод [1–5]. Энергия Гиббса GNano наночастицы определяется как

G

Nano

_ GBuUk + G$urface

где GBulk – энергия Гиббса объемной фазы с тем же составом и GSurface – дополнительная энергия Гиббса, связанная с поверхностным натяжением. Для расчета GBulk применяется метод CALPHAD с учетом дополнительного поверхностного давления. Стандартная энергия Гиббса наночастицы чистого i-го компо- нента определяется как

G0Nano _ G0 + CV i               ir

где c i - коэффициент поверхностной энергии, V_i – молярный объем, r – радиус частицы, С – поправочный коэффициент, связанный с формой частицы и поверхностной деформацией.

В этой статье предлагается более общий и более удобный подход к расчету химических потенциалов.

Обычно выражение для химического потенциала i-го компонента системы записыва- ют в виде

^_И 0 (T, P) + RT In a., (3) где T – температура, P – давление, ai – активность i-го компонента и ц0 (T, P) - некоторое произвольно выбранное эталонное значение химического потенциала (стандартный химический потенциал). Обычно мы не знаем истинного значения ц0 (T, P), но это не ме- шает использовать его для изучения химических реакций. Если каждый компонент рассматривать при одинаковой температуре и давлении, то определенная комбинация членов ц0 (T, P) компонентов частицы равна RT lnK (T, P), где R - универсальная газовая постоянная и K – константа равновесия, которая известна для многих реакций в макросистемах.

Однако, если мы изучаем химические реакции в системе различных микро- и наночастиц, мы не можем поступить таким обра- зом. Из-за поверхностных эффектов давление в частице и некоторые другие свойства зависят от размера частицы. Мы не можем комбинировать члены ц0 (T, P) компонентов для получения RT ln K (T, P) и использования химических потенциалов для изучения химических реакций среди малых частиц. Это ограничивает наши возможности изучать образование и рост наночастиц во многих областях науки и техники. В этой статье мы выведем выражение для химического потенциала с общим стандартным условием для всех частиц.

Термодинамические соотношения

Рассмотрим наночастицу, состоящую из m компонентов, как термодинамическую систему при температуре T и давлении P^e , оказываемом окружающей средой на систему. Запишем для нее фундаментальное уравнение Гиббса в виде

TdS _ dU + PdV -c ds - ^ ц i dn i ,      (4)

i = 1

где S – энтропия, U – внутренняя энергия, P - давление в частице ( P ^ P^e ), V - объем, c - коэффициент поверхностного (или межфазного) натяжения, который, в общем случае, зависит от размера частицы, s – площадь поверхности частицы, m – количество компонентов и n _i – количество молей i -го компонента.

Используя (4), мы можем записать полный дифференциал свободной энергии Гиббса

G _ U + PV - TS                  (5)

в виде dG _ -SdT + VdP + cds + ]m цdin..      (6)

i _ 1

Рассмотрим свободную энергию Гиббса как математическую функцию интенсивных переменных (T, P) и экстенсивных переменных (s, n1,...,nm). Химический потенциал цi зависит от этих же аргументов:

цi _цi (T,P, s, ni,..., nm), и его полный дифференциал может быть за- писан в виде d цРц dT +  dP +

' dT      dP m d^ +L ^d~dnj.

j ■ _i ^{d n}j

Так как из (6)

^ =4^1 дs дs l дni J

д дni

1^ 1 l дs J

ас д ni

и

= -S,,      = V,

д T     1  дP

где S_i и V_i – парциальная молярная энтропия и парциальный молярный объем i -го компо нента в системе. Используя (9) и (10), мы м ожем переписать (8) в виде

кой ( Р^е , 0 ) . Зададим линию интегрирования в виде ломаной (см. рисунок) с вершинами B ( P ^ф , s ^ф) , C ( P ^ф ,0 ) , D ( Р^е ,0 ) и получим

М D ) -н i ( B ) =

= J —(P, s) ds + V( P, s) dP

BCD i или

Mi( Pe ,0 )-н,( Pф, s ф) =

дс

d н i = VdP +—ds + (d н i )P ., д n-               P,s

где ( d н i ) _Ps — оставшаяся часть частных

дифференциалов d н i выражения (8), выраж ение ( d н i ) Ps равно 0 в процессах с постоя н-

ными T , n ₁ , ..., n_m .

Рассмотрим химический потенциал н i как математическую функцию интенсивных переменных ( T , P ) и экстенсивных переме нных ( s , n 1 ,..., n m ). Найдем приращение н i , когда давление P и площадь поверхности s изменяются от начального состояния ( P = P ^ф , s = s ^ф) к состоянию ( P = Р^е , s = 0 ) ,

= J дС (Pф, s ) ds + J V( P, s ) dP ,

s ф ‘ni              Pф ф e sф ‘С ф

н i =н i +        ( P , s ) ds +

⁰ д n i

+ J P V i ( P ,0 ) dP .                    (12)

при котором постоянными.

н i ( p e ,0 ) =_и е .

другие аргументы остаются Обозначим н i ( P ^ф , s ^ф) = н ^ф ,

Разность их равна кривол и-

нейному интегралу от d нi (P, s) вдоль линии фф с начальной точкой IP , s ) и конечной точ-

Зависимость поверхностного натяжения от размера частицы

Исследуем коэффициент поверхностного натяжения как математическую функцию интенсивных свойств ( T , P ) и экстенсивных свойств ( s , n ₁ , ..., n_m ) рассматриваемой системы. Поверхностное натяжение – интенсивное свойство системы; следовательно, с - однородная функция (степени 0) экстенсивных переменных s , n ₁ ,..., n_m , и мы можем записать [6]

с ( T , P , X s , X n i ,..., X n m ) =

= с ( T , P , s , n i ,..., n_m ) ,                     (13)

где X - произвольная постоянная. Положив

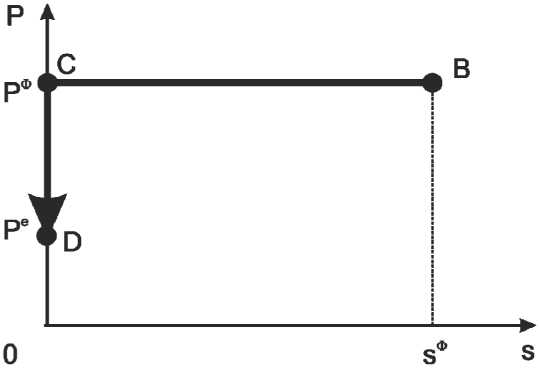
Линия интегрирования для криволинейного интеграла от дифференциала (11)

The path for line integral of the differential (11)

m

X = 1 n , где n = ^ n i - общее число молей в i = 1

частице, получаем

6 ( T , P , s , П 1 ,..., П т ) =

= 6 [ T , P , -, n ¹ ,..., n m ] .                (14)

к n n n J

Отметим, что ni- = Xi,                                 (15)

n где Xi – мольная доля i-го компонента. Учтя, что

где 5 - расстояние между поверхностью натяжения и эквимолекулярной поверхностью, 6 - поверхностное натяжение для плоской поверхности (в отличие от 6). Приведем это выражение к соответствию с (17). Так как r = 3 nv/s, (22) из (21) получим

6=

s ^,

1 + а

где а = — . Будем считать а постоянной ве-3 v

m

Z X i = 1,

i = 1

мы можем сделать вывод, что поверхностное натяжение может быть представлено в виде функции

6 = 6 I t , p , -, x 1 ,..., x_m - 1 1 . (17) к n J

Чтобы избежать путаницы, сразу отметим, что для сферической частицы радиуса R мы имеем

V = 4 n r 3 , s = 4 n r 2 , (18)

P ^ф _ p^ = 22. (19) r

В таком случае P и s становятся взаимно зависимыми; 6 не остается однородной функцией переменных состояния, и использование теории однородных функций некорректно. Поэтому, если мы используем теорию однородных функций, мы должны рассматривать P и s как независимые переменные и

личиной. Заметим, что по определению 6 не может зависеть от кривизны. Поэтому мы можем использовать (17) для 6 в виде

6 = 6 ( T , P , X 1 ,..., X m - 1 ) .                (24)

Теперь мы можем оценить первый интеграл в (12). Из (23) находим

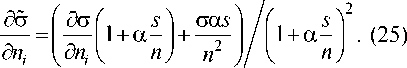
Принимая во внимание независимость 6

от s , получаем

г ^{s ф}д<7/ _ф \ n \ — I P , s ) ds =— J 0 5 ni ' а

, а 6

+ .

,    s ^ф    а

1 + а — n

г

учитывать различные зависимости только после получения конечных выражений.

Выражение (17) показывает, что площадь

поверхности s входит в наши уравнения только в составе комплекса s n . Заметим, что

выражение s n связано с кривизной поверх-

ности. В частности, для сферической частицы

s sv 3v n V r,

где v – средний молярный объем.

Найдем зависимость поверхностного на тяжения отs / n . Р.Ч. Толман [7] получил вы-

ражение

6 =

1 + ²⁵¹

r

, ф А

n ^56 6    ,

- —+- | ln 1 + а— +

s

a^d n i

n

к

ⁿ J

s ^ф

Так как а— очень мало ( 5 « r ) , мы можем n

использовать приближения

ln 1 + а—

к

1 s ^ф

1 + а— n

ⁿ J

s ^ф а—, n

1 s ^ф

1 -а— n

и получить гsф д6 / ф \56

Jo Г(P ,s)ds = zs .

J 0 5ni v '5

В соответствии с (15), (24) имеем d6 = m-1 d6 dXj = m-1 d6 5 ij - Xj=

5n, дX, dn      дX,n i J 1 j       iJ i m-1

=-Z6 ":гX)

ⁿ J = 1

и

Ф .              „Ф m -1

£ Н P * , * ) d ^S = “- '■^<’ f X j ) (30)

⁰ d п ,                n ~ ~ 1^y

, d' e    [0, если i ^ j где 'j =       и 5ij = 11        ■   • dXj          [1, если i = j

5 -функ-

ция Кронекера.

Химический потенциал компонента

частицы

Вернемся к формуле (12). Рассмотрим второй интеграл. В первом приближении для конденсированной фазы можно предположить, что молярный объем не зависит от давления, тогда

PФ fpe Vi(P,0)dP = Vi(PФ-Pe).         (31)

Используя (30) и (31), мы можем переписать (12) в виде

и ^: ,. e + v ( p ^ф - P ) +

Ф m - 1

+—E' ( ⁵ .j - j            (32)

ⁿ j = 1

Теперь определим физический смысл члена p. e . Химический потенциал является интенсивным свойством системы, следовательно, он является однородной функцией (степени 0) экстенсивных переменных. Точно так же, как мы получили выражение (17) для ст ,

lim p Ф =и i ( Т , P^e ,0, X 1 ,..., X m - 1 ) . (36) n ^W

Сравнивая (35) и (36), можно заключить, что pe - это химический потенциал объемной фазы того же состава и температуры, что и наночастица, но под давлением Pe . Используя (3), мы можем записать и e = и 0 (Т, Pe) + RT ln a„ (37) где ai – активность i-го компонента и и0 (T, P) - некоторое произвольно выбранное

эталонное значение химического потенциала (стандартный химический потенциал).

Основная идея определения физического смысла члена иe основана на следующем

рассуждении: площадь поверхности s входит в выражение химического потенциала (33)

ss только как —. Если n ^ » , то--> 0 ; тот же nn

для химического потенциала можно получить

и i = и i I t , p ,-, x 1

£ n

., ^л m - 1

В частности,

ф и i

, Ф

= и i t , P ^Ф , —, X 1

£ ⁿ

,..

., X m - 1

J

.

Член pe в (12) был определен как химический потенциал в гипотетическом состоянии с фиксированными значениями P = Pe и - = 0. Следовательно, мы можем заключить, что иe =pi (Т,Pe,0,X1,...,Xm-1). (35) С другой стороны, пусть общее число молей в (33) стремится к бесконечности при постоянных температуре и составе. В этом случае частица становится обычной объемной фазой; дополнительное поверхностное давление исчезает, PФ становится равным давлению Pe, оказываемому окружающей средой. Соотношение s n будет стремиться к нулю. Мы получаем из (34)

результат мы получим, если предположить - = 0. Таким образом, гипотетическое состояние с - = 0 без физического смысла эквивалентно реальному термодинамическому состоянию объемной фазы того же состава и температуры.

Подставляя (37) в (32), получим и Ф = и 0 (Т, Pe) + V-( p Ф- Pe) +

Ф m - 1

+—E' j ( 5 ij - X j ) + RT ln a_{ .       (38)

n j = 1

Отметим, что в нашем рассмотрении мы учли зависимость поверхностного натяжения от размера частицы. Однако конечное выражение (38) содержит не реальное поверхностное натяжение ст , а поверхностное натяжение для объемной фазы ст.

Если частица имеет сферическую форму, используя (18) и (19), получим и,Ф=и0 (Т, Pe)+2V + m-1

+-E' j ( 5 j - X j ) + RT ln a i .       (39)

r j = 1

Пример

В сталеплавильном производстве после расплавления шихты и окисления примесей расплав металла имеет избыток кислорода. Для удаления кислорода добавляют раскислители. Если используется алюминий, возможны следующие химические реакции:

2 [Al] + 3[O] = ( А120з ), [Fe]+[O]=(FeO)

и образуются наноразмерные зародыши продуктов реакций. Зародыши растут, и химические реакции (40) протекают на их поверхности. Растущие наночастицы состоят из раствора Al2O3-FeO. В окрестности поверхности частицы концентрации компонентов фазы расплава – Al, O, Fe – приходят в локальное равновесие с концентрациями компонентов фазы наночастиц – Al2O3, FeO .

Естественно, что концентрации компонентов фазы расплава в непосредственной близости от частицы не равны объемным концентрациям реагентов в расплаве. Это вызывает диффузионные потоки компонентов и доставку веществ для роста частицы.

Определим эти локальные равновесные концентрации реагентов на поверхности частиц разного размера и состава. Пусть температура расплава равна 1873 К. Воспользуемся следующими значениями [7]:

^c ai₂o₃ = 1,40 н/м, ^ FeO = 0,18 н/м,

^Al2O3 - 3,433 -10 5 м3/моль, VFeO - 1,562 ’10—5 м3/моль, aAl2O3         23

K Al2O3 -  2 3 -5 10 , aAlaO

K FeO = " FeO = 440. a Fe a O

Обозначим долю оксида алюминия в

Запишем условия равновесия для химических реакций (40):

2 ^ [ Al ] ^{+ 3} ^ [ O ] =^ ( Al₂O₃ ) , ^ [ Fe ] ⁺ ^ [ O ] = ^ ( FeO ) .

Используя выражение (3) для химических по- тенциалов компонентов расплава, получаем

^ [ Al ]^ [Al ] ( T , P e ) + RT ln X [ Al ] ,

H [ O ] =H [O ] ( T , P e ) + RT In X [ O ] , ^ [ Fe ] =^ [Fe ] ( T , P e ) ⁺

+ RT In ( 1 - X [ A ] - X [ o ] ) .

Воспользуемся выражением (38) для химических потенциалов компонентов частицы. Индекс 1 относится к Al ₂ O ₃ , индекс 2 относится к FeO . Получаем

»     It !2\^'"V A ^

^Ц ( Al₂O 3 ) =^ ( Al₂O 3 )⁽ T , P ^{) +} r ⁺

+ —— a' ( x )( 1 - x ) + RT ln x ,

r

U ⁰    (T P2 ² °^{( x} ) V ( Fe ^{O )}

^ ( FeO ) -^ ( FeO )⁽ T , P ^{) +} r

--— a' ( x ) x + RT ln ( 1 - x ) .

Подставляя (45), (46 ) в (44) и принимая во внимание, что

^ (Al₂O₃ ) ^- 2 ^ [Al ] ^{- 3} ^ 0O ] ^{- - RT ln} K ( Al 2 O₃ ) , ^ ( FeO ) ^- ^ (Fe ) ^- ^ 0O ] ^{- - RT} ln K ( FeO ) ’

частице через x ( x - Xai₂o₃ ) •

Считаем, что

получим систему уравнений:

зависимости поверхностного натяжения и молекулярного объема от состава частицы линейны:

X ² X ³     1

Al ^O -------exp x     K Al₂O₃

r 2 o V l2o₃+MM 1

\

rRT

v ^- ( V Al 2 O₃   V FeO ) ^{x +} V FeO ^-

( 1 - X Al

—

X oHo _-

1 - x

= 1,871 - 10 ^{- 5} x + 1,562 - 10 ^{- 5} ( м³/моль ) ,

° = ( ° Al 2 O₃ ^- ° FeO ) ^x + ° FeO =           ⁽⁴²⁾

= 1,22 x + 0,18 ( Н/м ) , o'- 1,22 ( Н/м ) .

Для простоты предположим, что активности компонентов частицы и расплава равны их молярным долям:

^a ( Al₂O₃ ) ^{- x} , ^a ( FeO ) = ^{1 x} , ^a [ Al ] ^- X [ Al ] ,

a [ O ] ^- X [ O ] , ^a [ Fe ] = ¹ - X [ Al ] - X [ O ] .

1 exp K FeO

(2o V_f„_o - 3 v o' x/

[ RT )

.

Для примера, решая эту систему с раз-

личными значениями r и x , принимая во внимание (41), (42), мы рассчитали таблицу.

Таблица позволяет сделать некоторые выводы о природе роста частиц. Например, предположим, что расплав содержит 0,1 % алюминия и 0,05 % кислорода ( X A ^lk - 0,001, X Ouk - 0,0005). В соответствии с таблицей расплав вблизи поверхности зародыша с ра-

Локальные равновесные концентрации реагентов у поверхности частицы радиуса r и долей оксида алюминия x

Local equilibrium concentration near the surface of the particle with radius r and alumina fraction x

r, м x 0,1 0,5 0,9 X[Al] X[0] X[Al] X[0] X[Al] X[0] 1-10-9 8,63E-08 2,51E-03 9,49E-06 2,97E-04 1,16E-02 3,14E-06 1 -10—8 1,17E-08 2,11E-03 8,53E-08 1,00E-03 1,99E-06 1,49E-04 1-10—7 9,56E-09 2,07E-03 5,33E-08 1,13E-03 8,36E-07 2,19E-04 1 -10—6 9,37E-09 2,07E-03 5,08E-08 1,15E-03 7,67E-07 2,28E-04 1 -10—5 9,35E-09 2,07E-03 5,06E-08 1,15E-03 7,60E-07 2,29E-04 1 -10—4 9,35E-09 2,07E-03 5,06E-08 1,15E-03 7,59E-07 2,29E-04 1 -10—3 9,35E-09 2,07E-03 5,1E-08 1,1E-03 7,59E-07 2,29E-04 диусом 10 нм и долей глинозема 0,1 имеет локальные концентрации алюминия и кислорода, равные X% = 1,17 -10-9, X0е = 0,00211. Поскольку XAC < XAulk, Xo > XOuk, алюминий будет диффундировать к поверхности частицы, а кислород – от поверхности. В результате доля оксида алюминия в частице увеличится, а доля оксида железа уменьшится. Частица с радиусом 10 нм и долей оксида алюминия 0,9 будет расти за счет поступления как Al , так и O. Изменение их состава будет определяться соотношением диффузионных потоков алюминия и кислорода на поверхности частицы.

Заключение