Расчет и исследование цветоделительных дифракционных решеток

Фазовые дифракционные решетки широко используются для разделения излучения различных длин волн по различным дифракционным порядкам [1-10]. Впервые так называемые цветоделительные дифракционные решетки были предложены Дамма-ном (H. Dammann) в 1978 году [1].

Для расчета цветоделительных дифракционных решёток в рамках скалярной теории разработан ряд аналитических и итерационных методов [1-10]. Наиболее общим аналитическим решением является цветоделительная решётка, позволяющая разделить три плоских волны с длинами волн

Л ° , Л ± 1 = Л ° N / ( N ± Р ) , Р eZ (1)

по –1, 0 и +1 дифракционным порядкам [4, 8-10]. Профиль такой решетки состоит из N ступенек равной ширины. Высоты ступенек определяются по формуле:

d i = r^^mod n ( “■ i ) , i = °, N - 1,         (2)

(n о - U где n0 - показатель преломления материала решетки, α - целое число:

N ■ m +1

a =------- , m e Z .

N + p

Разделение различных длин волн достигается за счет использования микрорельефа с высотой в N раз большей, чем при работе с одной длиной волны. Высота микрорельефа определяется близостью разделяемых длин волн. Чем ближе длины волн, тем больше N и тем выше требуется рельеф.

Цветоделительные решетки (2), (3) рассчитаны с использованием двух основных приближений. Расчет прохождения падающего пучка через решетку проводится в приближении геометрической оптики. Дальнейшее распространение светового поля описывается в рамках скалярной теории. При указанных допущениях интенсивности рабочих порядков решетки имеют вид:

I ° = 1, I +1 = I -1 = Sinc ² ( n / N ) .                   (4)

Интенсивности порядков определяют доли энергии излучения с длинами волн (1), направляемые в порядки 0, ± 1.

Вследствие большей в N раз высоты рельефа, для цветоделительных решеток актуальным является исследование ошибок, вызванных применением скалярного приближения и приближения геометрической оптики.

В данной статье приведены результаты исследования работы цветоделительных решеток (2), (3) в рамках строгой электромагнитной теории и результаты расчета цветоделительных решеток в рамках строгой теории с использованием градиентного метода. Представленные результаты позволяют установить границы применимости использованных приближений и оценить оптимальность решений, получаемых в рамках скалярной теории.

Метод исследования решеток в рамках электромагнитной теории

Для решения задачи дифракции на цветодели- тельной решетке в рамках строгой электромагнитной теории был использован метод связанных волн -RCWA метод (rigorous coupled-wave analysis method)

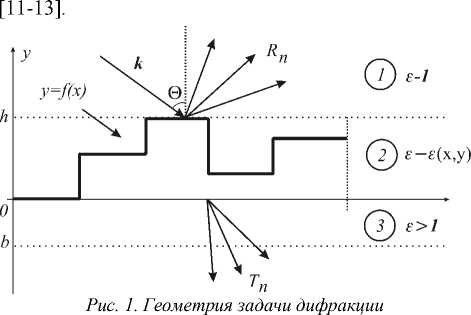
Согласно методу связанных волн введем три зоны (рис.1). Зона 1 соответствует области над решеткой при y > h , где h – максимальная высота микрорельефа. Зона 2 соответствует зоне модуляции

0< у < h , и, наконец, зона 3 соответствует области подложки у <0. Над решеткой и под решеткой диэлектрическая проницаемость постоянна. В зоне модуляции, диэлектрическая проницаемость является функцией е = е ( x,y ). Магнитную проницаемость будем считать равной единице во всех трех зонах. Согласно методу связанных волн поля в зонах 1 и 3 представляются в виде суперпозиции плоских волн с неизвестными коэффициентами отражения R n и пропускания T n . В зоне 2 поле ищется из решения уравнений Максвелла:

rot H = - ik ₀ е ( x , у ) E , rot E = - ik ₀ H .

Далее, коэффициенты отражения и пропускания в зонах 1 и 3 находятся из условия равенства тангенциальных компонент полей на границах зон при у = h и у =0. Метод связанных волн является стандартным и эффективным средством решения задач дифракции на периодических структурах.

Исследование влияния относительного периода и дрейфа волн

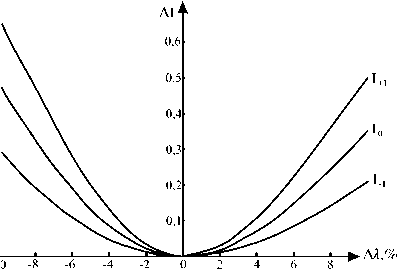
Известно, что скалярная теория дифракции правильно описывает распространение монохроматического излучения при характерных размерах объектов, на которых происходит дифракция светового пучка, много больше используемой длины волны. В нашем случае дифракция происходит на штрихах решетки, а удобным для использования характерным размером является период дифракционной решетки. Интересно исследовать границы применимости скалярной теории дифракции для цветоделительных решеток с малым (относительно основной длины волны 10) периодом. Для этого методом связанных волн были рассчитаны интенсивности прошедших дифракционных порядков для типичных цветоделительных решеток (работающих в видимом и ближнем инфракрасном диапазонах длин волн) в зависимости от размера периода. На рис . 2 приведены интенсивности рабочих порядков цветоделительной решетки (2) для разделения длин волн 1-1 = 0,7333 мкм, 1 = 0,55 мкм, 1+1 = 0,44 мкм (р =1, N=4) по порядкам -1, 0, +1. Интенсивности порядков приведены при различной величине периода от 510 до 5010 при нормальном падении, n0=1,5 для ТЕ и ТМ поляризации.

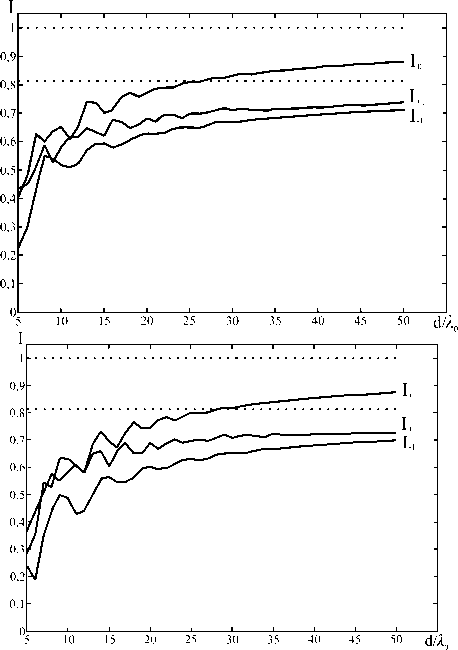
Рис. 2. Интенсивности рабочих порядков решетки (2) при p=1, N=4 в зависимости от величины периода для ТЕ (верхний график) и ТМ (нижний график) поляризации

На рис. 3, 4 приведены аналогичные графики интенсивностей рабочих порядков цветоделительной решетки (2) для разделения длин волн 1 .1 =0,6875 мкм, 1 0 =0,55 мкм, 1 +1 =0,4583 мкм (р =1, N =5) и 1 -1 =0,9167 мкм, 1 0 =0,55 мкм, 1 +1 =0,3929 мкм (р =2, N =5) по порядкам -1, 0, +1. Для решеток на рис. 3, 4 ( N =5) ошибка несколько больше, чем для решетки на рис. 2 ( N =4). Это связано с тем, что максимальная высота рельефа при N =5 в 1,33 раза больше, чем при N =4.

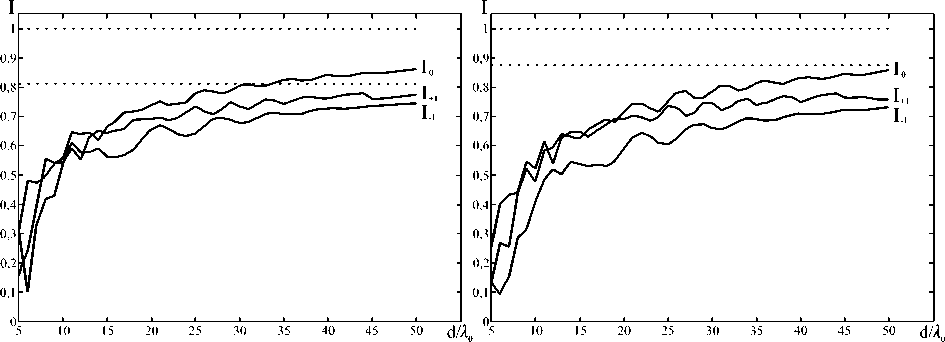
Рис. 3. Интенсивности рабочих порядков решетки (2) при p=1, N=5 в зависимости от величины периода для ТЕ (левый график) и ТМ (правый график) поляризации

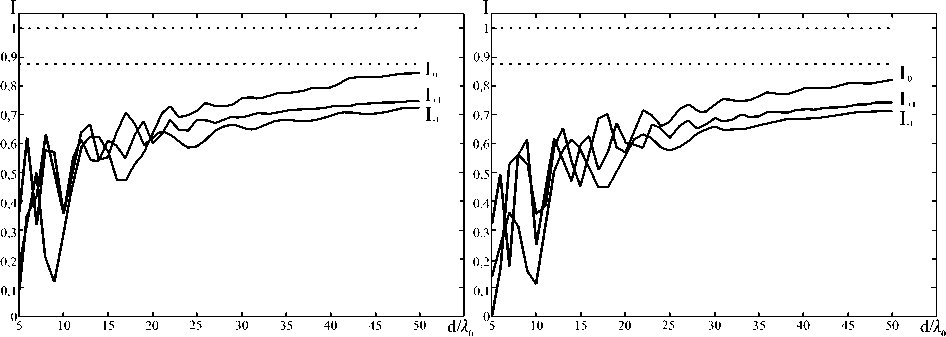
Рис. 4. Интенсивности рабочих порядков решетки (2) при p=2, N=5 в зависимости от величины периода для ТЕ (левый график) и ТМ (правый график) поляризации

Таким образом, при высоте дифракционного микрорельефа в 3-4 раза больше, чем при работе с одной длиной волны (при разности разделяемых длин волн в 20-25%), скалярная теория применима с ошибкой 10-15% только при периодах порядка 50 Х ₀ и более.

Как изменится работа цветоделительной решетки при освещении ее пучками с длинами волн, отличными от заложенных при расчете решетки? Для ответа на этот вопрос был проведен расчет интенсивности порядков в рамках скалярной и строгой электромагнитной теорий дифракции.

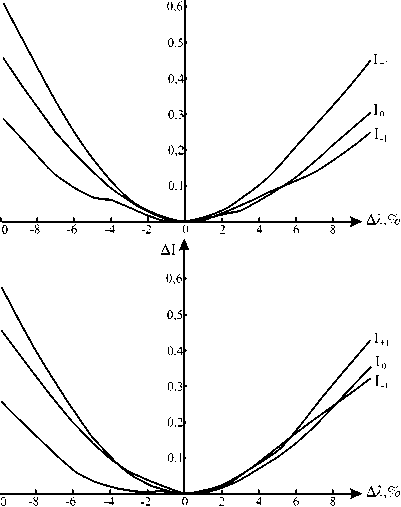
На рис. 5 приведены графики, демонстрирующие уменьшение интенсивностей рабочих порядков цветоделительной решетки при отклонении длин волн от расчетных значений. Графики на рис. 5а рассчитаны в рамках скалярной теории для решетки (2) при p =1, N =4. Графики показывают, что самым чувствительным порядком к изменению длины волны является +1-ый порядок. Интенсивность +1-го порядка уменьшается на 10% при изменении длины волны Х ₊₁ в пределах ± 3-4%. Эту тенденцию подтверждает и электромагнитная теория. На рис. 5б, в приведены графики уменьшения интенсивностей рабочих порядков решетки (4), рассчитанные в рамках скалярной теории и электромагнитной теории для ТЕ и ТМ поляризации при периоде d =15 Х ₀ .

Расчет решеток в рамках электромагнитной теории

Для оценки оптимальности аналитического решения (2), (3) был проведен расчет цветоделительных решеток в рамках строгой электромагнитной теории с использованием градиентного метода.

Поскольку профиль решетки (2) состоит из N ступенек, то в качестве параметров оптимизации использовались координаты и высоты ступенек. В качестве критерия оптимизация была использована функция

1 1 2

^е(x)=ЁЁ ( I j (x;^х i )^-5( j ^- i ) ) , ⁽⁶⁾ i =-1 j =-1

представляющая отличие расчетных l j ( x , 2 i ) ~ | T j |² и требуемых интенсивностей дифракционных порядков для длин волн (1).

а)

Д1М

б)

в)

Рис. 5. Уменьшение интенсивностей порядков решетки при отклонении длин волн от расчетных значений: а) в рамках скалярной теории при p=1, N=4

б, в) в рамках электромагнитной теории при p=1, N=4, d=15 X 0 для ТМ и ТЕ поляризации

Вектор x =( x₁,_,x_N-1 , ,h 1 , ..., h_N ) содержит набор параметров оптимизации, однозначно определяющих профиль решетки на периоде. Параметры 0< x i < x ₂<...< x_N -i < d являются координатами N ступе-

нек профиля, а параметры h i ≥ 0, i =1,…, N - высотами ступенек. Требуемые интенсивности порядков в (6) заданы функцией δ ( j-i ), равной 1 при i=j и 0 в противном случае. Вид функции ошибки (6) был выбран не только из условия максимизации рабочих порядков 0, ± 1 для длин волн (1), но и из условия минимизации перекрестного влияния рабочих порядков для различных длин волн.

Градиентный метод минимизации функции ошибки (6) состоит в итерационной коррекции вектора параметров профиля по правилу

x n = x n -1 - t ^V ^ (x) ,

( ^(x) ^д Ц x )

8 х 1

,...,

8 h N

- градиент функции

ошибки (6). Расчет градиента проводился численно по разностным формулам.

На рис. 6 приведены расчетные графики интенсивностей порядков цветоделительных решеток для разделения длин волн 1 -1 =0,6875 мкм, 1 0 =0,55 мкм, 1 +1 =0,4583 мкм (р =1, N =5), рассчитанных с помощью градиентного метода (6), (7).

а)

в)

д)

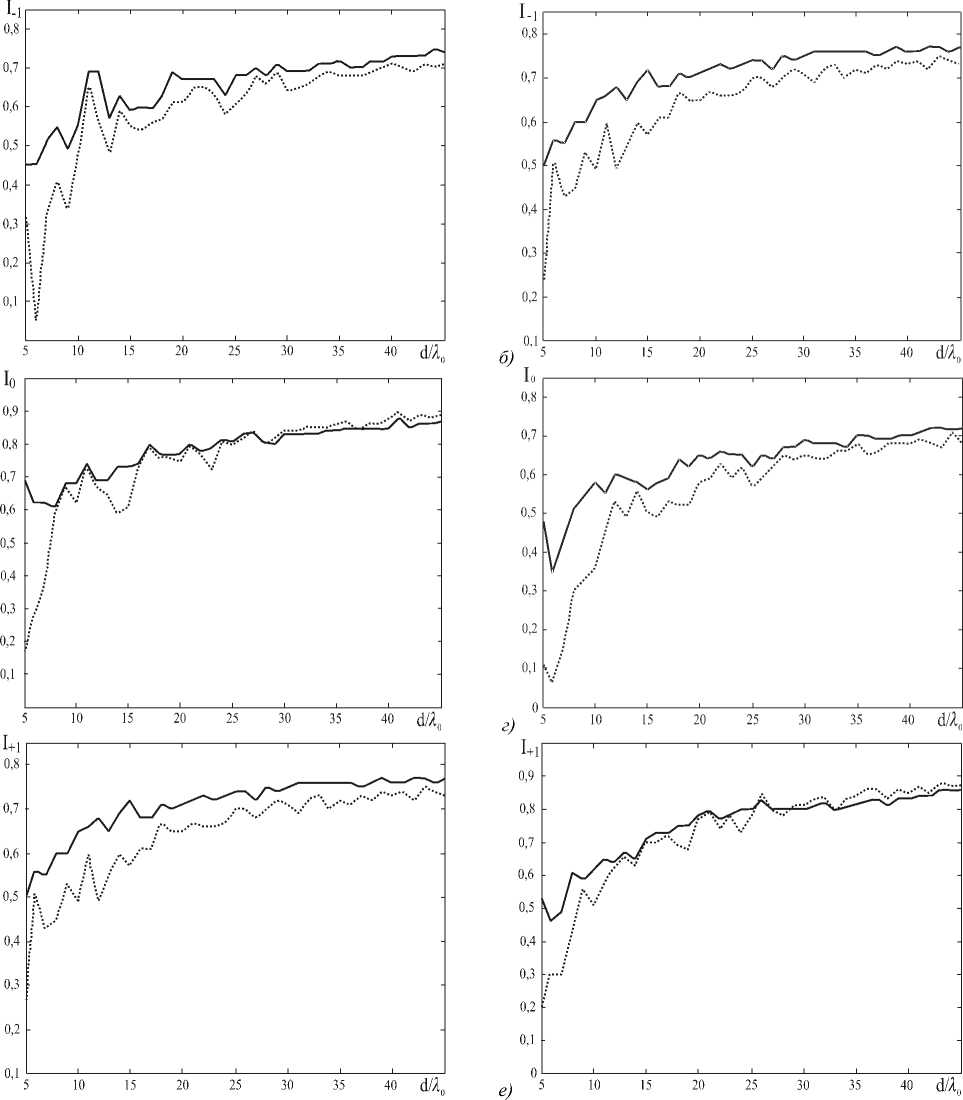
Рис. 6. Интенсивности рабочих порядков решеток, рассчитанных градиентным методом при p=1, N=5 в зависимости от величины периода для ТЕ (левые графики а, в, д) и ТМ поляризации (правые графики б, г, е)

В качестве начального приближения были использованы параметры профиля решетки (2). Графики интенсивностей приведены для различной величины периода от 5 λ ₀ до 50 λ ₀ при нормальном падении для ТЕ и ТМ поляризации. Пунктирными линиями показаны интенсивности порядков решетки (2), а непрерывными линиями - интенсивности порядков решетки после оптимизации. Пунктирные линии повторяют графики интенсивности на рис.3 и приведены для наглядности, разность между непрерывными и пунктирными линиями показывает увеличение интенсивности порядков, полученное за счет оптимизации профиля.

Графики на рис. 6 показывают, что градиентная оптимизация позволяет существенно увеличить интенсивность рабочих порядков (на 10-30%) только при малых периодах в 5-10 λ ₀ . С ростом периода до 50 λ ₀ увеличение интенсивности ± 1 порядков падает до 1-3%, а интенсивность нулевого порядка даже снижается на 0,5-1,5%. Таким образом, аналитическое решение (2), (3) является близким к оптимальному при периодах порядка 40 λ 0 и более.

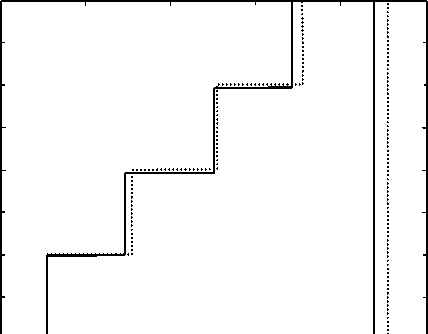
Приведем несколько примеров, иллюстрирующих графики на рис. 6. На рис. 7 показаны профиль цветоделительной решетки (2), (3) (пунктирная линия) и профиль решетки, рассчитанной градиентным методом при периоде d=10 λ 0 для ТМ-поляризации (непрерывная линия). Профиль, рассчитанный градиентным методом, получен при использовании аналитического профиля (пунктирная линия) в качестве начального приближения.

h/;0

I

Рис. 7. Профиль цветоделительной решетки (2) при p=1, N=5 (пунктирная линия) и профиль решетки, рассчитанной градиентным методом при d=10 X ₀ для ТМ-поляризации (непрерывная линия)

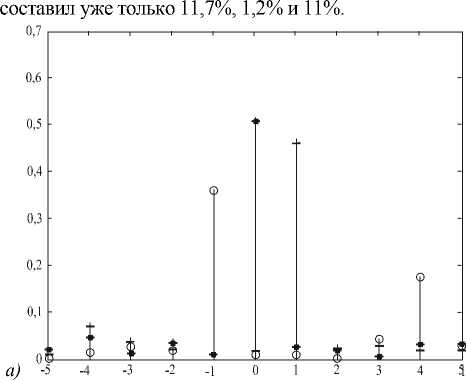
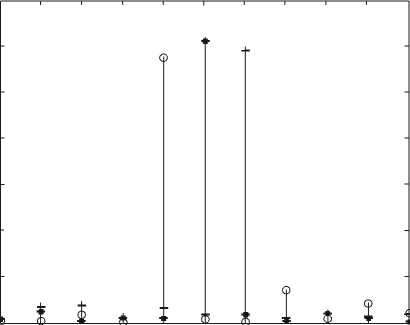
На рис. 8 символами «о», «*», «+», показаны интенсивности порядков решеток для рабочих длин волн. Для решетки (2), (3) интенсивности рабочих порядков –1, 0, +1 составляют 0,362; 0,5096; 0,4623; а для решетки, рассчитанной градиентным методом – 0,577; 0,612; 0,593.

На рис. 9, 10 приведены аналогичные результаты для решеток с периодом d=20λ0. Интенсивности рабочих порядков –1, 0, +1 для решеток на рис. 9 составляют 0,580, 0,766, 0,650 и 0,648, 0,775, 0,719, соответ- ственно. Сравнение рис. 8-10 показывает, что при периоде d=10λ0, применение градиентного метода значительно эффективнее, чем при периоде d=20λ0. При d=10λ0 градиентный метод позволил увеличить интенсивность –1, 0, +1 порядков на 59%, 20% и 28%, соответственно. При d=20λ0 рост интенсивности порядков

ол

0,6

б)  °-5     -4

0.2

-2

4     3

Рис. 8. Интенсивности порядков решеток на рис. 7 для рабочих длин волн (° - I-b * - I0, + - I+1) а) для решетки (2), (3); б) для решетки, рассчитанной градиентным методом

О'-----------------1------------------1------------------1-------------------1------^--------

О              0.2             0,4             0.6              0,8               1

Рис. 9. Профиль цветоделительной решетки (2) при p=1, N=5 (пунктирная линия) и профиль решетки, рассчитанной градиентным методом при d=20X0 для ТМ-поляризации (непрерывная линия)

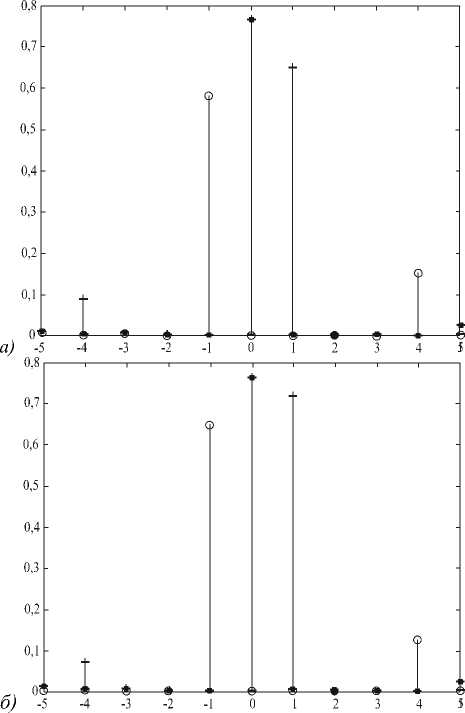
Рис. 10. Интенсивности порядков решеток на рис. 9 для рабочих длин волн (° -1 .1 , * - I₀, + -I₊₁) а) для решетки (2), (3); б) для решетки, рассчитанной градиентным методом

Заключение

Исследована работа цветоделительных дифракционных решеток в рамках строгой электромагнитной теории. Оценены границы применимости скалярного приближения и приближения геометрической оптики, используемых при расчете цветоделительных решеток. Показано, что при разности разделяемых длин волн в 20-25%, ошибка скалярной теории составляет порядка 50% для малых периодов с размером 5-15 λ 0 . При увеличении периода до 50 λ 0 ошибка скалярной теории снижается до 10-15%.

Проведен расчет цветоделительных решеток в рамках строгой теории с использованием градиентного метода. Оценена степень оптимальности решений, получаемых в рамках скалярной теории. Показано, что при малых периодах в 10-20λ0 применение градиентного метода эффективно и позволяет увеличить интенсивность рабочих порядков до 60-70%. При больших периодах в 30-50λ0 градиентная процедура не позволяет значительно улучшить аналитическое решение (2), (3).

Работа выполнена при поддержке грантов Президента РФ № МД-210.2003.01 и № НШ-1007.2003.1, гранта РФФИ № 04-01-96517 и российско-американской программы “Фундаментальные исследования и высшее образование” (BRHE).