Расчет и моделирование дифракционных структур для формирования двумерных интерференционных картин поверхностных электромагнитных волн

Одним из перспективных способов формирования микро- и наноструктур является фотолитография в ближнем поле, основанная на регистрации интерференционных картин затухающих или поверхностных электромагнитных волн (ПЭВ) [1–11]. Использование затухающих волн и ПЭВ позволяет преодолеть дифракционный предел и формировать структуры с размерами деталей в несколько раз меньшими, чем длина волны используемого света.

В работе [1] показана возможность получения одномерной интерференционной картины затухающих волн, соответствующих –1, +1 затухающим порядкам субволновой дифракционной решетки (ДР). Интерференционная картина в [1] обладает высоким контрастом. Интенсивность в максимумах интерференционной картины в 3–4 раза больше интенсивности падающей волны, а период — в два раза меньше периода ДР и составляет половину длины волны в [1]. В [2,3] рассмотрен аналогичный подход, основанный на использовании интерференции ПЭВ. Интерференционная картина ПЭВ формируется межд у щелями на поверхности перфорированной металлической пленки. В [4] предложен метод, основанный на интерференции затухающих волн, получаемых при полном внутреннем отражении. В [5–8] для формирования одномерных интерференционных картин ПЭВ используется ДР, расположенная над металлической пленкой.

В работе [9] рассмотрено формирование двумерных интерференционных картин ПЭВ. Инт ерферен-ционная картина формируется вдоль поверхности, ограниченной по краям двумя дифракционными решетками. Реш етки формируют ПЭВ, которые с границ решеток поступают в общую область, где и формируется соответствующая интерференционная картина. Основным недостатком данного подхода является малый размер области интерференции, ограниченный длиной распространения ПЭВ.

В [10,11] предложен метод, основанный на интерференции четырех затухающих волн. Период формируемых картин в [10,11] в 2–3 раза меньше длины волны. Затухающие волны формируются четырьмя падающими пучками с помощью полного внутренн его отражения. В [10] показана возможность управления структурой интерференционной картины за счет изменения поляризации и разности фаз межд у падающими волнами. Основным недостатком метода [10,11] является использование 4-х пучков. Для управления поляризаци ей и фазой пучков требуется сложная оптическая система.

В настоящей работе для получения интерференционной картины ПЭВ используется трехмерная дифракционная структура, состоящая из диэлектрической ДР и металлического слоя, нанесенного на подложку. В отличие от [9], размер области интерференции не ограничен длиной распространения ПЭВ. Предлагаемая структура более простая и компактная по сравнению с [10,11]. Результаты приведенных расчетов показывают возможность изменения частоты и конфигурации интерференционной картины за счет изменения поляризации и длины волны падающего излучения. Аналогичная структура была предложена в [6], однако в [6] не было исследовано качество формируемой интерференционной картины и влияние поляризации и длины волны на вид формируемы х картин.

Формирование двумерной интерференционной картины ПЭВ

Структура состоит из трехмерной бинарной диэлектрической ДР и металлической пленки, распо- ложенной под решеткой (рис. 1). ДР предназначена для возбуждения на границ е металлической пленки и подложки заданной композиции ПЭВ, которые формируют интерференционную картину.

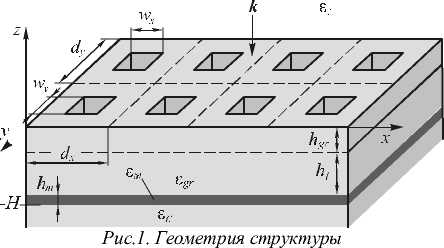
Рассмотрим случ ай нормального падения монохроматической электромагнитной волны на структуру. При этом проекции волновых векторов дифракционных порядков на плоскость Oxy имеют вид kn,m = J( 2Пndx )2 + ( 2Пmdy )2 ,

где dx, dy — периоды решетки, (n, m) — номер порядка. Условия возбуждения ПЭВ дифракционными порядками с номерами (±n ,0), (0, ±m) на границе раздела металлический слой-подложка имеют вид kn ,0 = Re (kspp ) = Re (k 0a);

k 0, m = Re ( k spp ) = Re ( k 0 ^a ) ,

гДе k spp = k 0 ^a = k 0 V ⁸ m ⁸ II /( ⁸ m ^{+ 8} II ) ^— константа распространения ПЭВ, где £ _m — диэлектрическая проницаемость металлической пленки, £_п — диэлектрическая проницаемость материала под металлической пленкой. Согласно (2), периоды решетки определяются по формулам:

^dx = ^{2 п} n / Re ( k spp ) , ^dy = ^{2 n} ml Re ( k spp ) .         ⁽³⁾

В работе рассмотрен случай n = m , при этом d_x = d., = d .

xy

Вид интерференционной картины ПЭВ зависит от поляризации падающей волны. Определим поляризацию углом у между направлением вектора E и осью Ox .

У ПЭВ вектор H лежит в плоскости границы раздела двух сред и перпендикулярен направлению распространения ПЭВ. Вектор E имеет ненулевую проекцию на направление распространения ПЭВ и лежит в плоскости, содержащей вектор направления и перпендикуляр к границе раздела сред, вдоль которой распространяется ПЭВ. Для возбуждения ПЭВ требуется, чтобы вектор E падающей волны имел ненулевую проекцию на направление распространения ПЭВ.

При нормальном падении волны с у = 0, (е = (Ex,0,0),H = (0,Hy,0)) ПЭВ будут возбуж даться порядками с номерами (±n ,0). Направления распространения у ПЭВ будут по оси Ox и вдоль оси Ox в отрицательном направлении. Аналогично, при у = 90° , (е = (0,Ey,0),H = (Hx,0,0)) и ПЭВ будут возбуждаться порядками с номерами (0, ±n). Направления распространения у ПЭВ буд ут по оси Oy и вдоль оси Oy в отрицательном направлении. В указанных случаях на нижней границе металлической пленки будут формироваться одномерные интерференционные картины.

Для формирования двумерных интерференционных картин необходимо возбуждение четырех ПЭВ симметричными дифракционными порядками с номерами ( - n ,0 ) , ( + n ,0 ) , ( 0, - n ) , ( 0, + n ) .

В этом случае падающая волна должна содержать перпендикулярные, направленные по осям O x , O y компоненты электрического поля. Этому условию удовлетворяет эллиптически поляризованная волна, соответствующая суперпозиции нормально падающих волн со следующими векторами электрического поля:

E 01 = ( ^E 0 x ^,0,0 ) ^ex P ^{( -} ik 0 ⁿI z ),

E ₀₂ = ( 0, E _{0 y} ,0 ) exp( - ik ₀ n I z + i 8 ),

где 8 — разность фаз, n I — показатель преломления материала в области над решеткой. Случаи 8 = 0 , 8 = л/ 2 соответствуют линейно-поляризованной волне и волне с круговой поляризацией. В дальнейшем б удем считать E 0 _x = cos ( у ) , E 0 _y = sin ( у ) . В этом случае вектор электрического поля падающей волны принимает вид

^ cos у ^

E =

sin у е‘ ⁸

\

exp( - ik ₀ n I z ).

Проведем анализ вида формируемой интерференционной картины при у = 45 ° и 8 = 0 . В данном случае падающая волна линейно поляризована и E _{0 x} = E _{0 y} . В силу симметрии дифракционной структуры комплексные амплитуды дифракционных порядков ( ± n ,0 ) , ( 0, ± n ) будем считать одинаковыми. В действительности, фазы дифракционных порядков могут отличаться, но это приводит лишь к сдвиг у интерференционной картины, а не к изменению ее вида. В дальнейших выкладках комплексны е амплитуды дифракционных порядков ( ± n ,0 ) , ( 0, ± n )

опустим.

Для ПЭВ, распространяющихся вдоль оси O x ,

HSPP = (0,Hy,SPP ,0) , ESPP =(Ex,SPP,0,Ez,SPP ) . Не- нулевые компоненты векторов HSPP, ESPP у ПЭВ, соответствующих порядкам (±n,0), могут быть получены из уравнений Максвелла в виде

H y , SPP ( x, z ) = cos ( k n x ) exp ( - ik z , n ( ^{z +} H ) ) ,     ⁽⁶⁾

E x , SPP ^{( x} , ^{z ) —}

^^^^^^s •

E z , SPP ^{( x} , ^{z ) —}

kn ik0е II

kz,n cos k0е II

(knx) exp (-ikz,n (z + H)), sin (knx) exp (-ikz,n (z + H)), где kn — 2nnd, kz,n — i*/kn

- k 02 Е _п . Отметим, что

приведенный вид k_{z , n} предполагает, что порядки ( ± n ,0 ) — затухающие.

Для ПЭВ, распространяющихся вдоль оси O y , H SPP = ( ^Hx , SPP ,0,0 ) , E SPP = ( 0, E y , SPP , E z , SPP ) . Ан^а логично, компоненты электромагнитного поля для ПЭВ, распространяющихся вдоль оси O y и соответствующих порядкам ( 0, ± n ) , имеют вид:

^Hx , spp ( У , ^z ) = cos ( ^kn y ) exp ( ^{- ik}z , n ( ^{z + H} ) ) ,     ⁽⁸⁾

kz,n cos

E y , SPP ^{( y} , ^z ) =

E z , SPP ^{( y} , ^{z ) —}

к0еii kn

-

ik 0 ^e II

(kny ) exp (-ikz,n (z + H)), sin (kny) exp(-ikz,n ( z + H)) .

Из (7), (9) получим компоненты электрического поля на нижней границ е металлической пленки (при z — - H ) в виде:

E x , SPP

k

( x , - H ) = - —— cos ( k n X ) , ^k 0 ^е II

E y , spp ( У , ^{- H} ) = 7 z ,^ co ^s ( ^kn y ) , ^k 0 ^е II

E z , SPP ( ^x , У , ^{- H} ) = T^ n - [ ^sin ( ^kn^x ) ^{- sin} ( ^kn y ) ] . i ^k 0 ^e II

В дальнейших расчетах в качестве материала металлической пленки используется серебро, а материала под пленкой — фоторезист с диэлектрической проницаемостью еII — 2,56. Диэлектрическая проницаемость решетки также была выбрана равной 2,56. При длине волны % = 550 нм значение диэлек- трической

проницаемости

с еребра

e m =- 12,922 + 0,44727 i . Для рассматриваемых материалов и длин волн выполняется неравенство

| ^Re {^e m } ^{+ e} II | » |M^e m }| .                        ⁽¹¹⁾

В этом случае имеют место след ующие приближения:

k_n k z , n

Re {^е m } ^е II

max|Ez,SPP (x,У,-H)|2 max|Ez,SPP (x, У,-H)|2 x, У _______________________ = x, У ______________________ max|Ex,SPP (x,-H)|      max|Ey,spp (x,-H)|

4IКе{е m }

— 4.

^е II

Согласно (13), вид интерференционной картины определяется компонентой E_{z , SPP} .

Для определения вида формируемой интерференционной картины необходимо найти экстремумы величины |EzSPP (x, y,-H)|2. Можно показать, что функция достигает максимумов в точках dlx x —     + , lx E ^,

2n4

dlyd

У — — +-- , l_y E Z

2n4

при условии, что l_x и l_y — разной четности. Максимумы функции | E_zSPP ( x , y , - H )|² и нули ее первых производных для n =3 представлены на рис. 2. В данном случае период дифракционной решетки определяется из соотношения (3) и равен 923 нм.

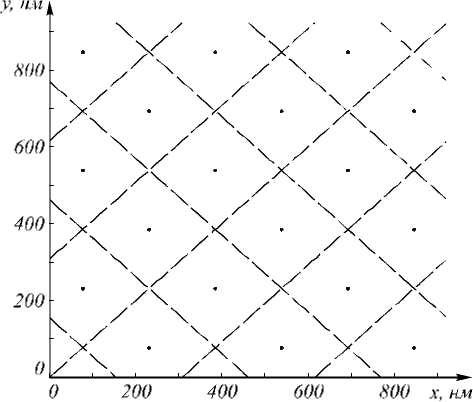
Рис. 2. Максимумы функции E z _sPPP ( x , y , - H )| 2 (точки) и нули ее первых производных (пунктирные линии) в случае линейной поляризации падающей волны

Согласно рис. 2 и (14), интерференционная картина повернута относительно координатных осей на угол в 45°, а ее период

d ip — V2 d / 2 n .

Рассмотрим теперь случай, когда падающая волна имеет круговую поляризацию. В этом случае с учетом разности фаз 8— л/ 2 в (5) компоненты электрического поля можно получить в виде

k

E x , spp ( x, ^- H ) = ^- i y²- cos ( k n x ) ;

k)E II

E y , spp ( У , - H ) = Tn²" cos ( к п У ) ;

k 0 ^E II

E_z , SPP ( x,У , ^{- H} ) = - k n -[ i sin ( k n x ) ^- sin ( ^кп У ) ] . ik q ^E II

Как и в случае линейной поляризации, вид интерференционной картины определяется компонентой E_{z , SPP} . Сравнение компонент E_{z , SPP} в (10) и

(16) показывает, что максимальное значение величины E zSPP ( x , y , - H )| 2 при круговой поляризации в два раза меньше, чем при линейной. Для определения вида интерференционной картины, как и в случае линейной поляризации, необходимо найти экстремумы величины E zSPP ( x , y , - H )| . Первые производные функци и равны нулю в точках

X = l g X;

4n x dly

У =     , l_y ^е 2,

4 n  ^y

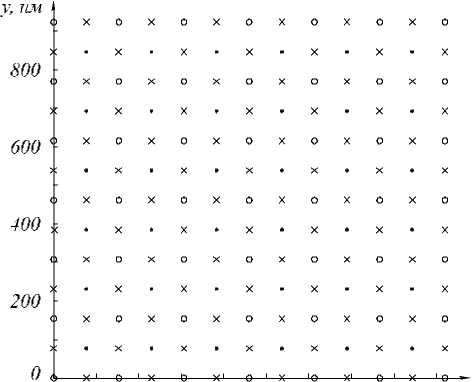
при этом минимумы достигаются при четных lx и ly , максимумы — при нечетных lx и ly . Экстрему- мы функции EzSPP (x, y, -H) и нули ее первых производных представлены на рис. 3.

О 200     400     600     800 х, нм

Рис. 3. Экстремумы функции E z _zSPP ( x , y, - H )| 2 ^т^чки — максимумы, кружки — минимумы) и нули ее первых производных (крестики) в случае круговой поляризации падающей волны

Согласно рис. 3 и (17), интерференционная картина ориентирована параллельно координатным осям, а ее период равен dip = d / 2 n.

Результаты моделирования

Расч ет интерф еренционных к арт ин ПЭВ проводился при следующих геометрических параметрах структуры: период d = 923 нм, w = 0,26 d , h_gr = 260 нм, h l = 0, h m = 70 нм (рис.1). Период был рассчитан из выражения (3) при n = m = 3. Отметим, что при использовании высших по рядков дифракции ( n >  1) периоды интерференционных картин (15), (18) в 2 n и 2 n раз меньше период а решетки. Это снижает требования к техно -логич еской реализации структуры и позволя ет формировать высокочастотные интерф еренцион-ные картины ПЭВ с по мощью низкочастотного дифракционного рельефа. З начения о стальных геометрических параметров структуры были определены с помо щью оптимизационно й процедуры, представляющей собой разновидность градиентного метода. Целевой функцией являлась мера близо сти рассчитанных интерференционных картин для случаев линейной и круговой поляризаций падающей волны к «идеальным» интерферен-цио нн ым картинам, формируемым при интерференции ч етырех ПЭВ.

Для расчета интерференционных картин использовался метод Фурье-мод (RCWA — rigorous coupled wave analysis) в формулировке работы [12].

На рис. 4 приведена рассчитанная интерференционная картина, формируемая непосредственно под металлической пленкой в случае TM-поляризации падающей волны ( E = ( E x ,0,0 ) , H = ( ), H_y ,0 ) ). ПЭВ при этом возбуждаются порядками с номерами ( ± 3,0 ) . Период картины равен 154

нм. Контраст и интенсивность в максимумах интерференционной картины, нормированная на интен-

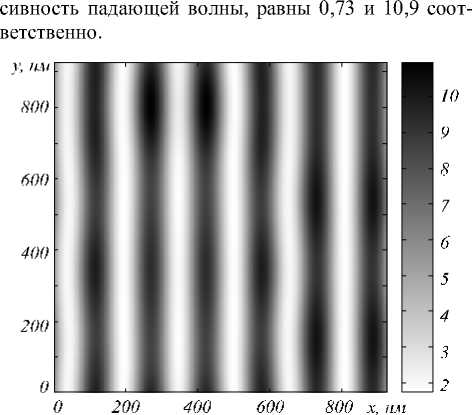
Рис. 4. Распределение интенсивности электрического поля под металлической пленкой в случае TM-поляризации падающей волны ( V = 0 ° )

На рис. 5 и 6 приведены рассчитанные интерференционные картины, формируемы е непосредственно под металлической пленкой для случаев линейной и круговой поляризации падающей волны. Период интерференционной картины в случае линейной поляризации падающей волны равен 218 нм и 154 нм в случае круговой поляризации. Значения контраста и нормированной интенсивности электрического поля в максимумах интерференционной картины составляют ( 0,99;20 ) и ( 0,73;10,9 ) соответственно. Структура рассчитанных картин совпадает с теоретически полученны ми видами на рис. 2 и 3. Отметим, что периоды формируемы х интерференционных картин в 2,52 и в 3,57 раз меньше длины волны падающего излучения для случаев линейной и круговой поляризации соответственно.

О 200    400     600    800 х, нм

Рис. 5. Распределение интенсивности электрического поля под металлической пленкой в случае смешанной линейной поляризации падающей волны ( у = 45 ° , 5 = 0 )

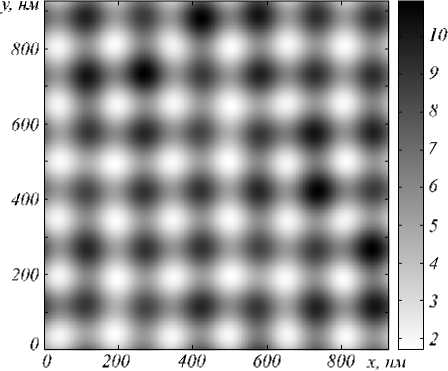
Рис. 6. Распределение интенсивности электрического поля под металлической пленкой в случае круговой поляризации падающей волны ( у = 45 ° , 5 = 90 ° )

В общем случае угол у может быть отличным от 45°, что соответствует различным амплитудам TE- и TM-компонент. Также возможна элли птиче- ская поляризация волны, когда разность фаз между TE- и TM-компонентами отлична от 0° и 90°.

Рассмотрим два примера. На рис. 7 представлена рассчитанная интерференционная картина для случая, когда падающая волна имеет линейную поляризацию, а угол у = 20°. Контраст формируемой интерферен- ционной картины равен 0,86, а максимальное значение нормированной интенсивности электрического поля в максимумах картины — 16,6. Хорошо видно изменение вида картины по сравнению с рис. 5. Интерференционные максимумы на рис. 7 имеют более вытянутую, эллиптическую форму.

0     200    400     600     800 х, им

Рис. 7. Распределение интенсивности электрического поля под металлической пленкой в случае линейной поляризации падающей волны ( у = 20 ° , 5 = 0 )

На рис. 8 приведена рассчитанная интерференционная картина для эллиптически поляризованной падающей волны. Амплитуды TE- и TM-компонент в этом случае равны, а разность фаз межд у ними составляет 50°. Интерференционные максимумы на рис. 8 имеют близкую к ромбовидной форму. Контраст формируемой интерференционной картины равен 0,83, а нормированная интенсивность электрического поля в максимумах картины — 17.

0      200     400     600     800 х, им

Рис. 8. Распределение интенсивности электрического поля под металлической пленкой в случае эллиптической поляризации падающей волны ( у = 45 ° , 5 = 50 ° )

Таким образом, предложенная структура позволяет формировать двумерны е интерференционные картины ПЭВ, обладающие высоким контрастом. Возможно управление видом формируемы х картин за счет изменения поляризации падающей волны. Значение нормированной интенсивности электрического поля в максимумах картин превышает 10.

Управление пространственной частотой интерференционной картины

Рассмотрим возможность управления частотой интерференционной картины за счет изменения длины волны падающего излучения. Пусть период решетки d определен из условия возбуждения ПЭВ порядками с номерами ( ± n ,0 ) , ( 0, ± n ) при длине волны % :

d = 2 п n /Re ( k spp ) . (19)

Константа распространения ПЭВ k_spp = k_spp ( % ) зависит от длины волны. Поэтому возможно возбуждение ПЭВ при другой длине волны % ^ X с использованием дифракционных порядков с номерами ( ± m ,0 ) , ( 0, ± m ) , m ^ n . Длины волн, которые буд ут возбуждать ПЭВ порядками с номерами ( ± m ,0 ) , ( 0, ± m ) , могут быть найдены из уравнения

%'= d Re ( « ( %' ))/ m , (20) где а= Re ^ £ _m £ II /( е _m + £ II ) . В частности, для рассмотренного случая % = 550 нм , n = 3 , ПЭВ будут возбуждаться ±2 порядками при длине волны 774 нм. На рис. 9 и 10 приведены рассчитанные интерференционные картины, формируемые непосредственно под металлической пленкой для случаев линейной и круговой поляризации падающей волны. Значения контраста и нормированной интенсивности электричес кого поля в максимумах интерференционной картины составляют ( 0,99;76,6 ) и ( 0,85;38,7 ) соответственно.

0 200 400 600 800 х, н.м

Рис. 9. Распределение интенсивности электрического поля под металлической пленкой в случае смешанной линейной поляризации падающей волны при λ ’=774нм

.         .         .         .

0     200     400     600    800 х, нм

Рис. 10. Распределение интенсивности электрического поля под металлической пленкой в случае круговой поляризации падающей волны при X = 774 нм

Заключение

Предложен способ получения двумерных интерференционных картин ПЭВ с помощью дифракционной структуры, содержащей трехмерную диэлектрическую дифракционную решетку и металлический слой. Результаты моделирования в рамках электромагнитной теории показывают, что рассматриваемая структура позволяет формировать интерференционные картины с высоким контрастом (более 70%) и высокой интенсивностью. Интенсивность интерференционных максимумов на порядок превышает интенсивность падающей волны. Период интерференционных картин в 2,5–3,5 раза меньше длины волны. Вид рассчитанных картин совпадает с аналитически полученными оценками. Результаты расчетов показывают возможность получения интерференционных картин с различной структурой, периодом и формой интерференционных максимумов при изменении параметров поляризации и длины волны падающего света. Рассмотренная структура может использоваться для производства наноструктур на основе регистрации интерференционных картин ПЭВ методом контактной фотолитографии.

Работа выполнена при поддержке грантов РФФИ № 09-07-92421-КЭ_а, 08-07-99005-р_офи, 07-0196602, 07-07-91580-АСП_а, гранта Президента РФ № НШ-3086.2008.9, «Фонда содействия отечественной науке», российско-американской программы «Фундаментальные исследования и высшее образование» (PG08-014-1).