Расчет и моделирование оптических систем с использованием поверхностных волн

Поверхностные электромагнитные волны нашли широкое применение в современных оптических приборах. Их уникальная способность к локализованному распространению вдоль границы раздела сред используется в датчиках оптических свойств среды, в оптической микроскопии, при контроле рельефа поверхностей, в оптических волноводах [1-8].

В настоящей статье рассматривается простая оптическая система для формирования высокочастотной интерференционной картины. Система состоит из дифракционной решетки и металлической пленки, расположенной в области подложки. Использование высших, симметричных дифракционных порядков решетки с номерами ± m , m >  1 для возбуждения плазмонов позволяет получить интерференционную картину с частотой в 2 m раз выше, чем у исходной решетки. Такой подход кажется авторам перспективным для задач фотолитографии. Использование интерференции плазмонов дает способ записи фотошаблона высокочастотной дифракционной решетки на основе дифракционной решетки с “большим” периодом.

Статья состоит из двух частей. В первой части излагаются общие сведения о поверхностных волнах и способе из возбуждения. Во второй части описана система с дифракционной решеткой для возбуждения и интерференции поверхностных волн.

Общие сведенияо поверхностных волнах

Поверхностные волны несложно получить из решения уравнений Максвелла rot H = - ik08 E

rot E = ik 0 H    (1)

для двух сред. Будем считать, что граница раздела сред с диэлектрическими проницае-мостями ε ₁, ε ₂ находится в плоскости Oxy и совпадает с осью Ox . При этом решение уравнений (1) для случая ТМ-поляризации имеет вид [7]

( X, У ) = ( Ex , Ey ,0) exP ( ikxx + ^ У ) , H(j) (x, y) = (0,0, Hz) exp (ikxx + ikyj)y), (2) где =1,2 – индекс среды, p. p

ε ₁ ε ₂

^kx   ^k 0a           ,

\ 81 + 8 2 ’

( k ) = k '2 8, - k x ,             (4).

k ₀ = 2-п / X, X — длина волны в вакууме. Уравнения (2) определяют плоские волны в средах 1, 2, а условия (3), (4) получены из условия непрерывности тангенциальных компонент полей на границе раздела сред.

Если существуют такие ε1 , ε2 , что компонента k вещественна, а компоненты k( j) -xy мнимы, то решение (2)–(4) определит волну, распространяющуюся вдоль границы раздела (оси Ox) и экспоненциально затухающую по оси Oy. Такого рода электромагнитные волны носят название поверхностных волн. Эти волны могут существовать на границе раздела сред с разными знаками диэлектрических проницаемостей и только для ТМ-по-ляризации [7,8].

В оптическом диапазоне поверхностные волны могут существовать на границе раздела “металл–диэлектрик”. В качестве металлов используются хорошие проводники (Au, Ag, Cu) для которых действительная часть ε отрицательная и большая по модулю, а мнимая часть – положительная и небольшая. В данной статье расчеты проведены для золота, у которого при X = 630нм £ = - 20,86 + 0,28i.

Для возбуждения поверхностной волны используют стеклянную призму с металлической пленкой на основании (рис. 1). Призму освещают ТМ-поляризованной волной

Hz ( ^x , У ) = exP ( i ( ^k о x x ^{+ k} о у У ) ) =

= exp ( ik ₀ ^£ r ( sin ( 0 ) x — cos

где θ – угол падения, ε_pr – диэлектрическ ая проницаемость материала призмы. Поверхностная волна формируется на нижней границе раздела между металлической пленкой и воздухом при некотором угле падения θ_PL [8]. При этом угле наблюдается резкий минимум коэффициента отражения от металлической пленки.

Угол θ_PL оказывается близким к углу, при котором выполняется условие равенства x -компонент волновых векторов в падающей и

Рис. 1. Схема возбуждения поверхностной волны

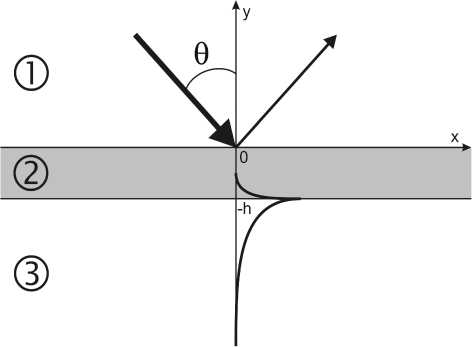
Рис. 2. Модель для расчета условий возбуждения поверхностной волны

поверхностной волнах [7, 8]:

1 εε sin (0PL )~^= J—     (6)

V £ pr N ^£ i ^{+ £} 2 ^{.        (6)}

Формула (6) не учитывает толщину пленки. Более точные аналитические оцен- ки угла θPL приведены в [8]. В общем слу- чае, для точного расчета угла падения θPL , обеспечивающего минимум отражения, используется модель с двумя полубесконечны-ми областями над и под металлической пленкой (рис. 2). Допустимость такой модели объясняется тем, что призма на рис. 1 не дает вторичных отражений.

Поле в этой модели описывается следующими выражениями:

H .4^x , y ) = exp ( i ( ^k о xx ^— k> y ) ) +

+ Rexp ( i ( к _{0 x}x + k ^¹ y ) ) , H i ² ) ( ^x , У ) = A ^exP ( i ( ^k 0 x x ^{— k}y ^{2 )} У ) ) ⁺

+B exp (i (k0 xx + ky2) y)), Hi3 (x, у ) = T exP (i (kо xx - ky3) у )), где (k(,j)) = k02£j — k,2x, а индекс j обозначает номер среды. Компоненты электрического поля находятся дифференцированием компо-

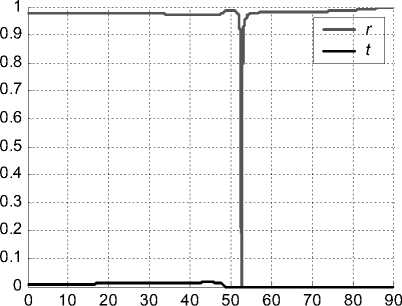
Рис. 3. Интенсивности отраженной и прошедшей волн в зависимости от угла падения

r ₂₃ , τ ₁₂ , τ ₂₃ – коэффициенты отражения и пропускания на соответствующих границах раздела сред:

r pq

= ^S q^k _y p ) — ^S p k q ) ^S q^ky p ^{)+ S} p^ky q ) ,

τ

2S q k y p ¹

S q k ,p ' + S p k ,q ' -

Уравнения (9), (10) показывают сложную зависимость коэффициентов R и T от параметров от ε ₁ , ε ₂ , ε ₃ , h и θ .

нент H ( j ) , j = 1,2,3:

e «)=- JL -H ik0s dy ’

На рис. 4 приведены расчетные графики интенсивностей отраженных и прошед-

ших волн

( r ~ | R |², t ~ T |²)

в зависимости от

j i dHj y ik0s dx "

Используя граничные условия на границах раздела сред, несложно получить систему линейных уравнений относительно коэффициентов R , A , B и T . При этом коэффициенты отражения и пропускания имеют вид [8]:

R =

r 12

+ r 23 e

i 2 k,²> h

1 + r ₁₂ r ₂₃ e

2 k У ²> h

T =

τ 12 τ 23 e ^y

1 + r ₁₂ r ₂₃ e

2 k , ²> h

угла падения θ . Графики рассчитаны для золотой пленки ( s ₂ = - 20,86 + 0,28i ) с толщиной h = 58нм при длине волны X = 630нм, s ₁ = 4, s ₃ = 2,25. Известно, что металлы в оптическом диапазоне хорошо отражают излучение. Рис. 3 показывает резкий минимум отражения при угле падения 0 PL = 52,58°. При этом угле происходит возбуждение поверхностной волны, которую принято называть плазмоном .

Рис. 4 показывает, что при тех же условиях наблюдается максимум плотности энер-

где h – толщина металлической пленки, r12 , гии электрического поля (WE ~ T )

в зоне

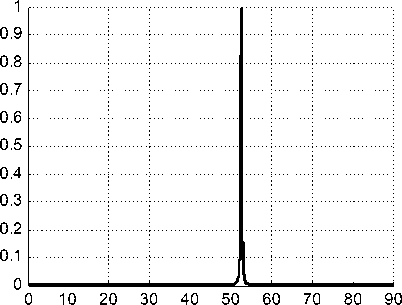
Рис. 4. Нормированная плотность энергии электрического поля в зависимости от угла падения света

под металлической пленкой.

Возбуждение плазмона возможно только при условии s ₁ >  s ₃ [7,8]. Значение угла θ_PL , при котором наблюдается минимум отражения, также зависит от диэлектрической проницаемости среды ε ₃ под металлической пленкой. На рис. 5 приведен расчетный график этой зависимости при вышеуказанных параметрах.

Участок этой кривой до _s ® 3 показывает квазилинейную зависимость угла θ_pl от ε ₃ . Эффект зависимости θ_pl от ε ₃ использу-

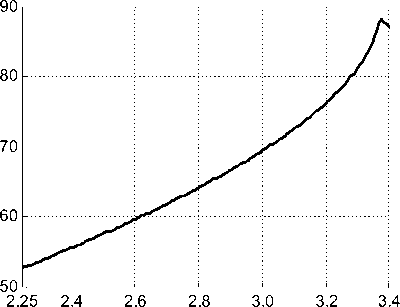
Рис. 5. Зависимость угла минимального отражения θPL от ε3

Поскольку в рассматриваемых случаях хороших проводников | e ₂1 0 e₃, то контрастность близка к 1. Период интерференционной картины будет таким же, как у функции sin² ( ^k 0 x x ) , ^т.е.

dPL

π

λ

2 ε ₁ sin θ_PL ^,

ется в датчиках мониторинга оптических свойств среды в зоне под металлической пленкой.

Формирование дифракционной решеткой высокочастотной интерференционной картины плазмонов.

Если в модели возбуждения плазмона (рис. 2) рассмотреть не одну, а две симметрично падающих волны

В данной работе для получения интерференции двух плазмонов предлагается использовать дифракционную решетку, расположенную над металлической пленкой (рис. 6). На рис. 6 показана простейшая бинарная решетка с одним штрихом на периоде.

При нормальном падении света на дифракционную решетку, отраженные и прошедшие порядки с номерами ±m расходятся под симметричными углами sin0m = mX / Ved, (16)

H 0 Z ’ ( x , У ) = exp ( i ( k 0 x x ^— k y¹ У ) ) + + exp ( - i ( k 0 x^x + k^’У ) )

(11) где k 0 x = k 0 Je ^ sin ( 0 ) , то в этом случае в зоне 3 будут возбуждаться две встречные поверхностные волны. В результате интерференции этих волн поле под пленкой примет вид:

H 3 ( x , У ) = 2Te - "k^У>y cos ( k 0 x x ) , (12)

Согласно (8), (12), плотность энергии

где λ – длина волны падающего излучения, m – номер порядка, d – период решетки, ε – диэлектрическая проницаемость среды, в которой происходит распространение. При симметричном профиле решетки амплитуды порядков с номерами ± _m будут также одинаковы. Поскольку возбуждение плазмона происходит при строго определенном угле падения θ_PL , то дифракционные порядки, распространяющиеся под другими углами, не смогут пройти через золотую пленку.

Выберем период решетки в виде

электрического поля W_E ~ E ² под пленкой в

mλ d =------ n sin θ_PL ^.

этом случае имеет вид

^WE ( x , У ) ~ ^( ^k 0 x ² -| ^ky ^3>| ) ^Sin 2 ( ^k 0 x x ) ⁺ I k ^l ) ^X x exp ( - 2 | ^k<³⁾| у )

, (13)

Выражение (13) описывает интерференционную картину, затухающую по оси О y . Используя оценку (13), несложно получить контрастность интерференционной картины

K =

W E max

—

W E min

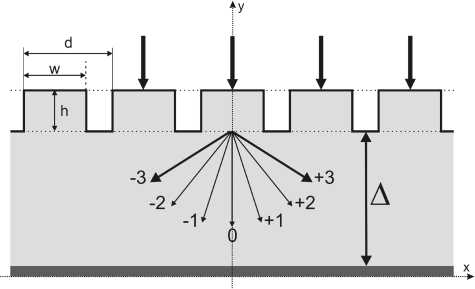
Рис. 6. Бинарная решетка с металлической пленкой

W E max

+ WE^min

^

2 ε ₂

^{( e} 2 ^{+ e} 3 )

— 1 .

При этом дифракционные порядки с номерами –m, +m сформируют поверхностные волны на нижней стороне металлической пленки. При этом период dPL интерференционной картины этих волн будет в 2m раз меньше, чем период исходной решетки d / dPL = 2m. (18)

Это позволяет использовать решетку с периодом d для получения интерференционной картины с периодом в 2 m раз меньшим, чем у исходной решетки. Данный эффект может быть использован для изготовления высокочастотных решеток литографическим способом.

Отметим, что уравнения (17), (18) дают свободу выбора номера порядков m . С ростом номера m период решетки, которую можно использовать для синтеза более высокочастотной, растет, однако, при этом доля энергии, которую удается направить в ± m порядки, как правило, уменьшается.

За счеты выбора геометрических параметров профиля решетки (ширины w и высоты h ступеньки) можно повысить интенсивность дифракционных порядков, используемых для возбуждения плазмонов. Для m =3, X = 630нм, ₈ = 4 (диэлектрическая проницаемость материала решетки) и при ранее указанных условиях возбуждения плазмона ( h = 58нм, 0 PL = 52,58 ° , е ₂ = - 20,86 + 0,28i, 8 3 = 2,25), период решетки должен быть равным d = 1190_нм. Отметим, что используемо е значение диэлектрической проницаемость в

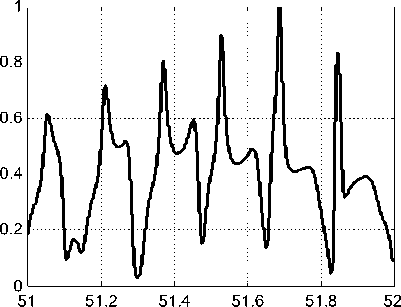
Рис. 7. Зависимость максимальной амплитуды плотности энергии электрического поля за пленкой от толщины подложки д (мкм)

зоне за пленкой 8 3 = 2,25 соответствует диэлектрической проницаемости стандартных фоторезистов. Максимальная интенсивность дифракционных порядков 1 3 = I _{- 3} = 11,3% достигается при w = 0,7 d , h = 0, 86X . Параметры w, h были найдены простым перебором значений. При этом для расчета интенсивностей порядков использовался метод связанных волн (rigorous coupled-wave analysis) [9-11]. Данный метод решения уравнений Максвелла является модификацией дифференциального метода и позволяет моделировать процесс дифракции световой волны на диэлектрических и металлических дифракционных решетках со сложным профилем периода [9-11]. Еще одним параметром оптимизации является толщина подложки д , определяющая расстояние от решетки до золотой пленки. Как правило, существует спектр значений д , обеспечивающих высокие значения амплитуды плотности энергии поля за пленкой. На рис. 7 приведен нормированный график максимальной амплитуды плотности энергии поля в зависимости от параметра д . Максимальное значение достигается при Д = 51,69мкм .

На рис.8 представлено распределение энергии электромагнитного поля в зоне под металлической пленкой, полученное для рассмотренной решетки. Распределение также рассчитано по методу связанных волн. Размер области наблюдения совпадает с периодом d = 1190нм по оси Ox и имеет размер d /2 = 5951 1 по оси Oy .

Рис. 8 показывает четкую интерференционную картину с в 6 раз более высокой частотой. Период интерференционной картины составляет d_PL =198нм.

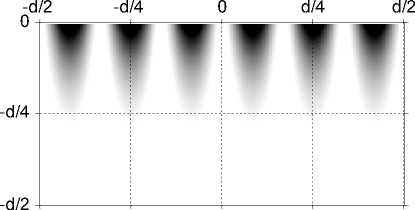
Рис. 8. Плотность энергии электрического поля под металлической пленкой на одном периоде решетки

Данный пример показывает перспективность использования подобной оптической схемы в литографии для получения высокочастотных решеток.

Заключение

Проведенное исследование показывает возможность использования системы из дифракционной решетки и металлической пленки для формирования высокочастотной интерференционной картины плазмонов. Приведенные результаты расчета и моделирования системы показывают высокое качество интерференционной картины при шестикратном уменьшении периода.

Работа выполнена при поддержке гранта РФФИ № 04-01-96517, гранта CRDF RUE1-005064-SA-05, министерства образования РФ, Администрации Самарской области, гранта CRDF SA-014-02, гранта ИНТАС N 0477-7198.