Расчет и моделирование регулировочной характеристики шланговой задвижки

Таипова Дилара Раисовна, старший лаборант.

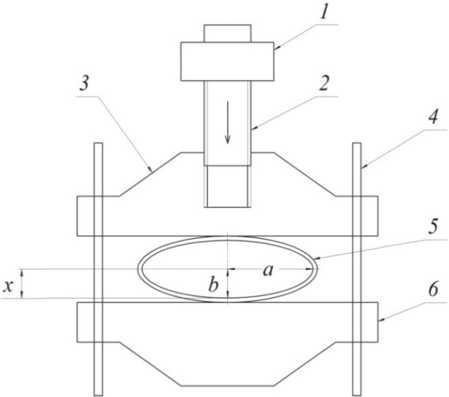
Рис. 1. Схема шланговой задвижки:

1 – подшипник, 2 – винт от управляющего двигателя, 3 – траверс, 4 – направляющие, 5 – эластичный канал, 6 – корпус, x – величина деформации шланга, a , b – геометрические размеры сечения шланга

Шланговая задвижка регулирует поток жидкости путем сдавливания эластичного канала 5, что изменяет геометрические параметры пропускного отверстия. Под действием винта от управляющего двигателя 2 происходит смещение траверса 3 по отношению к корпусу задвижки, тем самым изменяется форма и площадь сечения пропускного отверстия. При расчете считаем, что сечение при сжатии принимает форму овала, а максимальный размер пропускного отверстия достигается при отсутствии сжатия и определяется площадью окружности S =π r ₀ ² , где r ₀ – радиус не сдавленного шланга. Под регулировочной характеристикой понимается зависимость пропускной способности от перемещения перекрывающего траверса шланговой задвижки.

Для использования шланговой задвижки в системах управления необходимо получить за-

кон изменения площади сечения пропускного отверстия шланговой задвижки от величины деформации x эластичного канала. Пропускная способность определяется площадью отверстия

режимах малого пропускания задвижки) имеют место большие погрешности. Например, при б = 1, относительная погрешность приближения (3)

шланговой задвижки, которая определяется как

площадь эллипса S = πax в сжатом виде, и как площадь круга S ₀ = π r ₀ ² при отсутствии сжатия. Степень открытия q шланговой задвижки опре-

делится как отношение

q =

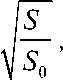
0 ≤ q ≤

1,0 .

Очевидно, что длина окружности поперечного сечения шланга при деформации не изменяется. Длина оболочки эллипса определяется

при ограничении двумя членами ряда составит Y = 25%, что недопустимо много для моделирования процесса. Приближение эллиптического интеграла тремя членами ряда (3) не позволяет получить аналитического решения уравнения (2). Тем не менее, для получения прямого аналитического решения уравнения (2) воспользуемся следующей методикой. Обозначим:

- (1 - -^)sin² P d p = f (-) .   (4)

aa

п

I

по формуле [7]:

п

²                      _f Л ^

L = 4 at 1 - - £ ² sin² вdP = 4 aE I — , £ I , (1)

о                                  ^{X 2    J}

Проведем расчет функции f ( - / a ) , полагая, что всегда 0 ≤ x ≤ a (см. рис. 1). Представим данные в виде таблицы 1.

График функции f I —

X a J

имеет вид, пока-

где

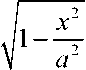
эксцентриситет (смотри

рисунок 1), p - промежуточный параметр инте-

( л грирования, E I —, 8 - эллиптический инте-

занный на рис. 2 (кривая 1).

Уравнение линейной аппроксимации кривой 1, полученное в программе MATHCAD имеет вид (прямая 2):

f ( ^- ) « 0,944 + 0,59 ^- . aa

грал второго рода. За начало координат принят центр эллипса, где х = 0 .

Из условия равенства длины контура эллип-

са и окружности шланга в исходном состоянии составим уравнение, связывающее в общем

виде конструкционные параметры задвижки при сжатии пропускного канала:

Максимальная погрешность линейной аппроксимации, определенная в той же программе, составляет у = 5.6%, в точке х/а=0. Точность не высока, однако, выражение (5) позволяет получить «грубый» закон регулирования задвижки. Подставляя (5) в уравнение (2), получаем:

4 a (0,944 + 0,59 ^- ) = 2 л r₀ . (6) a

п I------

4 a I \ 1 — (1

x ²

—2 ) sin² pdp = 2 пг ₀ . (2) a ²

Отсюда

2 пг - 2,36 -a =     ⁰

3, 776

= 1,664 r₀ - 0,625 - .

Для получения регулировочной функции шланговой задвижки необходимо в явном виде получить зависимость а от х . Интегральное уравнение (2) не имеет точного аналитического решения. Приближенное аналитическое реше-

ние возможно при разложении эллиптического

интеграла (2) в ряд, который имеет вид:

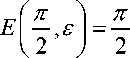
- - 1 т

X 2 J

1 - 2 V £ 4

2 - 4 J 3

. (3)

При ограничении в разложении (3) двумя членами ряда при б ^ 1,0 (при х ^ 0, то есть в

Определяя площадь эллипса, получим закон изменения площади пропускного отверстия от перемещения траверса задвижки:

S ( - ) = п -a = л х 2 ^{П Гй - 2,36 -} = 5,228 xr„ - 1,9635 -²

3,776        ^{,      0 ,}         _{, (7)}

при этом 0 ≤ х ≤ r ₀ .

Степень открытия шланговой задвижки

определяется как относительное изменение пропускной способности по формуле:

I S ( - ) = 1 5,228 r ₀ - - 1,9635 -² =

q (- ) =

\ ^S 0      V          ^{л г} 02

Таблица 1

x a	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
f ( xa )	1	1.016	1.051	1.096	1.151	1.211	1.276	1.346	1.418	1.493	1.571

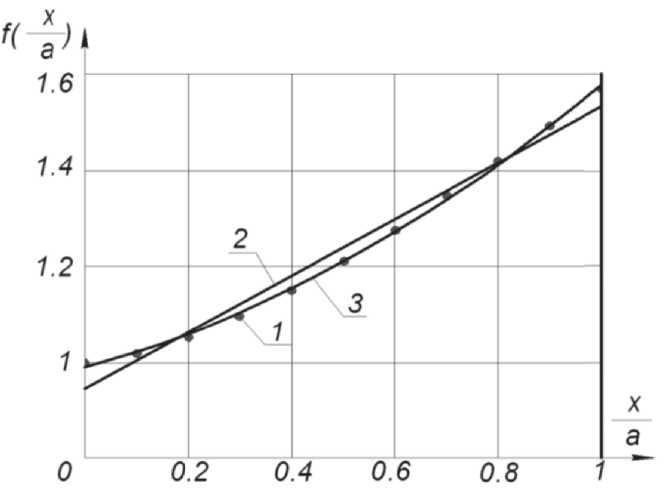
Рис. 2. График эллиптического интеграла 1 и его алгебраическая аппроксимация: 2 - линейная, 3 - квадратичная

= 1,664 - - 0,625( x )² . (8) N r o r o

Проверяем: при x = r ₀ , q ( x ) = 1,019 . В идеальном случае q ( r ₀ ) = 1,0 . Таким образом, погрешность моделирования закона регулирования шланговой задвижки при линейной аппроксимации эллиптического интеграла (4) составляет 1,9 %, что вполне приемлемо для большинства технических задач. Результаты расчета по формуле (8) пропускной способности шланговых задвижек, имеющих разные размеры r ₀ , представлены на рис. 3.

Для более точного моделирования воспользуемся квадратичной аппроксимацией эллиптического интеграла (4) (кривая 3 рисунка 2):

f ( x ) « 0,989 + 0,293 x + 0,297( x )² . (9) aaa

Максимальная погрешность аппроксимации Y = 1.1%, в точке х/а=0.Подставляя (9) в уравнение (2),получаем:

4 ^ [0,989 + 0,293 x + 0,297( x )² ] = 2 п r₀ .

aa

О 0,025 0,05 0,075 0.1 0,125 0,15 0,175 0,2 0,225 0,25 хм

Рис. 3. Зависимость пропускной способности шланговой задвижки q от перемещения x траверса при различных размерах шланга

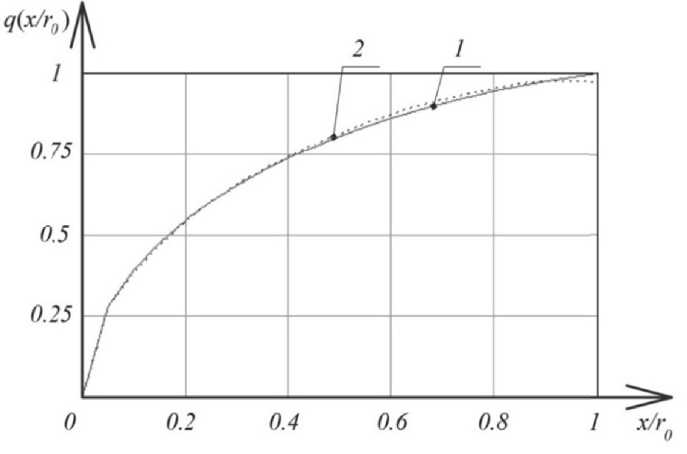
Рис. 4. Графики пропускной способности q ( x ) шланговой задвижки в зависимости от перемещения траверса х, полученные по формулам (8) – кривая 1, и (12) – кривая 2

a² + 2(0,148 x - 0,794 r₀) a + 0,3 x ² = 0 .

Отсюда a = (0,794r0 - 0,148x) ±

± 7 (0,794 r ₀ - 0,148 x )² - 0,3 x ² . (10)

В выражении (10) оставляем «+» из условия того, что при х = r ₀ , a = r ₀ .

Определяя площадь эллипса, получим более точный закон изменения площади пропускного отверстия от перемещения траверса задвижки:

S ( x ) = nxa = nx [(0,794 r ₀ - 0,148 x ) +

+ 7(0,794 r ₀ - 0,148 x )² - 0,3 x ² ] . (11)

при этом 0 ≤ х ≤ r ₀ .

Степень открытия шланговой задвижки определяется как относительное изменение пропускной способности по формуле:

q ( x ) =        =

• V nr 0

Полученные данные описывают статическую характеристику задвижки, которая позволяют организовать процедуру автоматического управления при медленных изменениях давления и скорости потока. При быстрых изменениях давления и высоких скоростях потока необходимо учитывать динамические характеристики, связанные с учетом деформационных процессов в жидкости, трубах и подводящей арматуре.