Расчет и моделирование тепловых потерь в термических печах с многослойной футеровкой

Для выбора оптимальных технико-экономических показателей термических печей с многослойной футеровкой при их проектировании целесообразно провести исследование и моделирование тепловых потерь через свод, под и стенки печи. Это важно не только для выявления истинной картины тепловых потерь, но и для установления температурного режима работы каждого слоя печи, что позволит обоснованно выбрать огнеупорные и теплоизоляционные материалы каждого слоя футеровки, а также их толщину.

Исследование влияния толщины одного из слоев кладки печи как на тепловые потери, так и на температурный режим работы всех слоев проведем на примере печи с четырехслойной футеровкой, выполняя моделирование тепловых потерь через каждый из слоев стенки.

Пусть задано: Z_BH, Я_вн, 5_ВН - длина, высота и ширина внутреннего пространства печи; S_b A, S₃ и А - толщины отдельных слоев футеровки (рис. 1).

Л = 0,98 + 0,000278+ л,)/2 ;

2-й слой - шамот-легковес (ШЛ-0,9),

А =0,4+ 0,000383-(r12 +Z23)/2;

3-й слой - перлит вспученный в порошке,

А = 0,06 + 0,000186- (Z23 + Z34) / 2 ;

4-й слой — шамот легковес (ШЛ-0,9),

A = 0,4 + 0,0003 83-(t34+ZHap)/2.

Для исследования влияния толщины одного из слоев, например, третьего слоя на тепловые потери и на закономерность изменения температуры между слоями следует выразить толщину этого слоя через переменную.

Алгоритм реализации моделирования в системе Mathcad следующий:

• 1)    Необходимо задать внутренние размеры стенки печи и толщину слоев в метрах:

явн=1     Ан =2

А =0,23 S₂ =0,115 S₄ =0,115;

• 2)    Определить размеры футеровки по диаго

  

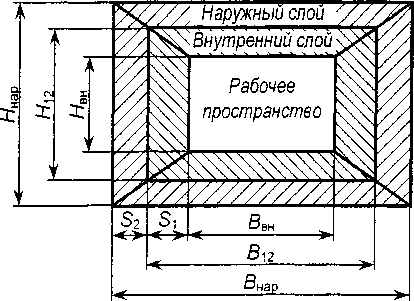
  Рис. 1. К расчету параметров печи

  
  

Неизвестными являются температура между слоями кладки и наружная температура стенки: /_|2, ?₂₃, ^34, 4и_Р, а также тепловые потери через стенку Q„.

Для реализации численных методов расчета пяти неизвестных необходимо составить пять уравнений, описывающих тепловые потери через каждый из слоев и через наружную стенку, которые, естественно, равны между собой. Предварительно необходимо выразить размеры футеровки по диагональным стыкам слоев, выбрать огнеупорные и теплоизоляционные материалы каждого слоя кладки и выразить теплопроводность каждого слоя в функции материала и средней температуры слоя [1].

Например: 1-й слой - шамот класса А (ША), средняя теплопроводность слоя нальным стыкам слоев:

Аг = Ан + 2 • А Аз = Аг + 2 ■ А

Ад = Аз + 2 • S3 А = Ад+ 2 ■ А

Я₁₂=Я_вн+2-А Я₂₃=Я₁₂+2-А Я₃₄=Я₂₃+2 А я₄ =я₃₄+2-А;

• 3)    Выразить толщину третьего слоя в виде функции:

А, = 0,025-(l + z/25), где г=0...200;

• 4)    Задать исходные данные и первое приближение неизвестным:

Ар = 20     /_вн = 1000      a = 12

?нар = 30      /12 = 700

?23 = 600     А4 =300      2ет=1200;

• 5)    Составить и разрешить, используя вычислительный блок системы Mathcad, систему пяти уравнений, описывающих тепловые потери через каждый из четырех слоев и наружную стенку:

бет = 7Явн Ан ' Vя! г Аг х х 0,98 + 0,000278 • Al±A

I                      2

бот -       ' 7Я|2 Д2 ' 7ягзАз х

X 0.4 + 0,0003 83-^-^- ,

( ’                       2 Г бет - 23 „ 3 '^23By -^Н34В34 X

X О,06 + 0,000186 • ^1^1 ;

• (                    2 ;

бет =^^-7^Г-7здх

X 0,4 + 0,0003 83^ ;

• (                   2 J

бет ^— (/нар ^— 4 ) ’ ® Н^Вд .

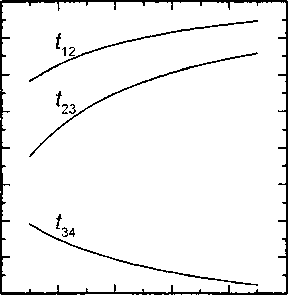
Моделирование с использованием этого метода позволяет не только найти искомые неизвестные для любого частного значения толщины третьего слоя, но и наглядно представить закономерность изменения тепловых потерь, а также температур между слоями, в функции дискретного значения S3, что и проиллюстрировано на рис. 2 и 3. На рис. 2 представлена закономерность изменения тепловых потерь в функции толщины третьего слоя, а на рис. 3 - закономерность изменения температур между слоями, позволяющие анализировать и обоснованно подбирать многослойную футеровку печи.

Если выделить внутри футеровки элементарный слой толщиной AS = S/N, где N - большое число разбиений, то, используя численный метод, можно найти закономерность изменения температуры внутри каждого слоя. Численный (итерационный) метод решения системы уравнений, записанных для всех слоев футеровки, позволяет установить истинную картину изменения температуры футеровки, которая представлена на рис. 4. Ниже представлен алгоритм определения закономерности изменения температуры футеровки (здесь / = 1. ..NY

• .       __1

• * 0 ~ “’ 1,-114 0,98+0,000278+, В H, " N* 4-1     4-14-1

t₂ = („, b =+₂ —-----------------—---

• ⁰    А       ₀,4 + 0,000383+_2] ^,Я_2|1 N

• 4    =43; 4 =4 —------------—-;

• ⁰               o, 06 + 0,000186+₃    В H₃ N

0,0 0,1 0,2 0,3 0,4 0,5 0,6

S

Рис. 4. Изменение температуры в футеровке

s3

Рис. 2. Изменение тепловых потерь

_ 500 400

0,00 0,05 0,10 0,15 0,20 0,25 s3

Рис. 3. Изменение температур между слоями

Интенсивность падения температуры футеровки зависит от теплового сопротивления кладки. Если вновь воспользоваться итерационным методом и выразить текущее тепловое сопротивление каждого слоя:

R = —!

0,98 + 0,000278+^ В^,

R21

'   0,4+ 0,000383 •/₂. _। В₂Н₂.

r3 =---------

' 0,06 + 0,000186+з    В₃.Н₃₁

R =................ 1—,

¹   0,4 + 0,000383+_4]. _i В₄.Н₄.

то мы получим наглядную картину закономерности изменения текущего теплового сопротивления каждого слоя футеровки (рис. 5).

Корягин Ю.Д., Сердега Ю.П.

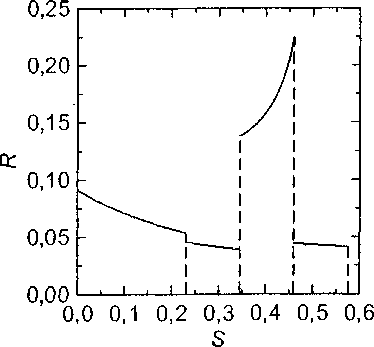
Рис. 5. Изменение теплового сопротивления многослойной футеровки

Расчет и моделирование тепловых потерь в термических печах с многослойной футеровкой

Таким образом, моделирование тепловых потерь в функции частного значения толщины одного из слоев с использованием ПЭВМ позволяет наглядно представить закономерность изменения тепловых потерь и температур как между слоями, так и внутри футеровки. Анализируя эти закономерности, можно обоснованно подбирать многослойную футеровку печи при ее проектировании.