Расчет и проектирование микрополосковых согласующих элементов

Такие элементы, как симметричный скачок ширины проводника в микрополосковой линии (МПЛ), находят самое разнообразное применение в согласующих трансформаторах, фильтрах, соединительных элементах и т.п. Эскиз скачка ширины МПЛ представлен на рисунке 1.

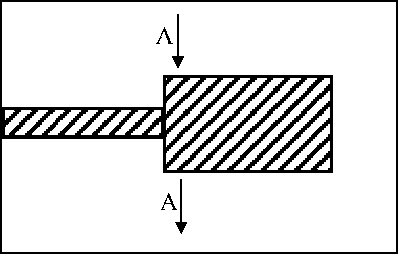
Рис. 1 Эскиз скачка ширины МПЛ

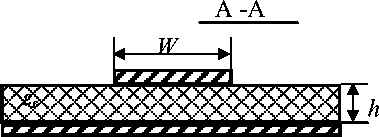
Расчет параметров и размеров и размеров МПЛ проводился на основе модели Олинера. В этой модели диэлектрическая проницаемость диэлектрика заменяется эффективной проницаемостью, размеры полосков эффективными размерами, а боковые стенки диэлектрика заменяются магнитными стенками.

Эффективная диэлектрическая проницаемость ^0 рассчитывается по формуле [1,3,4]

^£ эф 0

Sr + 1

+

^S r

- 1

1 +

10 h

- 1

V

V

W

где h =толщина слоя диэлектрика, W - ширина полосковой линии, s - диэлектрическая проницаемость подложки.

В общем случае, особенно на очень высоких частотах, диэлектрическая проницаемость зависит от частоты. На основании обобщения многочисленных экспериментальных результатов получена следующая эмпирическая формула, позволяющая сравнительно просто учесть дисперсию основной волны в МПЛ [1,2,3].

^- эф

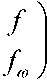
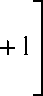
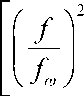
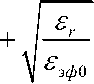
Г -,

где / -рабочая частота, ГГц; — ^ - определяется по формуле (1);

( 16 . 2 — ^{0 . 25} )

f = 3 . 5 +        r—^r.

^Jй        ,  0 . 12W e ⁰³⁵

1 +----- r—

h

Расчет размеров скачка ширины полосковой линии проходил по формулам приведенным в [3,4] . Если волновое сопротивление обозначить через Zв, ширину полосковой линии W, а высоту подложки с диэлектрической проницаемостью —. через h, то волновое сопротивление вычисляется по формуле:

W

• 1)    при <  1 h

  
  
  
  
  
  
  
  

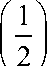
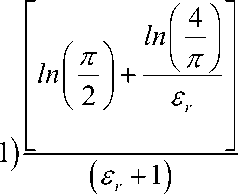
W

• 2)    1) при >  1 h

  Z в =

  
  
  
  
  

  W               8 -1  ,     . 4

  + 0 . 441 + 0 . 882 -^ + — + 1)---

  2 h                  - ^{2 V} r 2 2-е

  
  

  - 1

  
  
  
  

Размеры МПЛ по заданному Zв рассчитываются из следующих выражений

• а)    при d > 2.1

  W/h =

  
  

  8_;

  (e^d - 2 e"^d )

  
  
  
  

• б)    при d ≤ 2.1

W/h = 2 (d - 1 )/ n - 2 ln( 2 d - 1 )/ n + ( e - 1 ) fln(d_x - 1 ) + 0 . 293 - 0 . 517 / e ] /( л^ )

где d = (Z, / 60Ц(г, +1)/2 + (e, -1)(0.226 + 0.12/s,)/(e, +1);

• d , = 60 n ² /(Z , J7, ).

Для дальнейшего расчета и исследования скачка ширины МПЛ выбирались следующие исходные параметры:

Z_e = 50 Ом; e =7.2; h = 1 мм.

Расчет проводился в среде Maxima по формулам (5) и (6).

Рассчитанные размеры скачка приведены на рисунке 2.

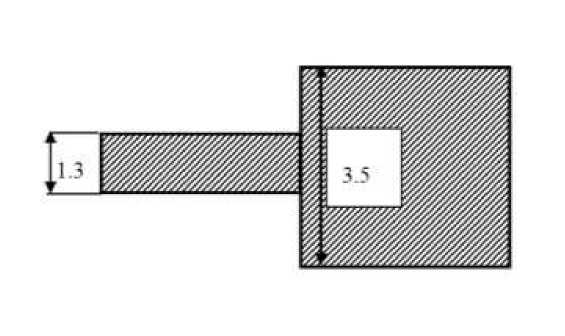
Рис.2. Размеры скачка ширины МПЛ

Была рассчитана матрица рассеяния для скачка ширины линии МПЛ

[2,4 ]

Z -- Z.  2л Z Z , в2        в1              в2   в1

2л IZ.Z .   Z, - Z.

в 1 в 2         в 1         в 2

где

D =

s

Z в I + Z в 2

Коэффициент стоячей волны по напряжению (КСВН) Kst можно оценить по формуле:

^K st

На рис.3 представлена зависимость КСВН от частоты.

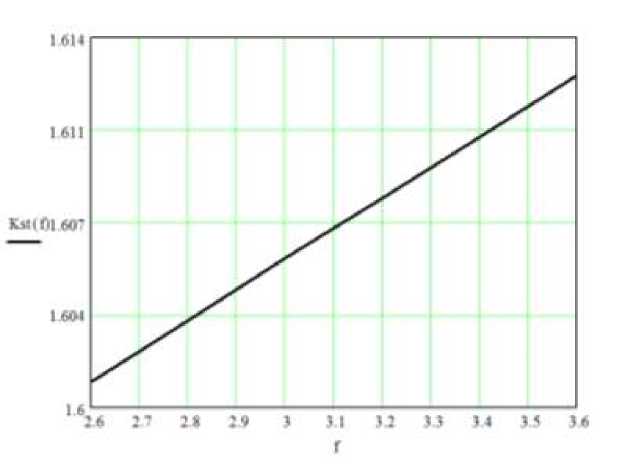
Рис.3. Зависимость КСВН от частоты f в (ГГц)

Скачок ширины полоска был промоделирован в среде «Microwave office», внешний вид показан на рис.4.

Рис.4. Топология скачка ширины МПЛ с плоскостями разгерметизации

Были получены кривые элементов матрицы рассеяния и КСВН, вид которого показан на рис.5. Кривые, полученные в результате расчета и моделирования достаточно близко совпадают.

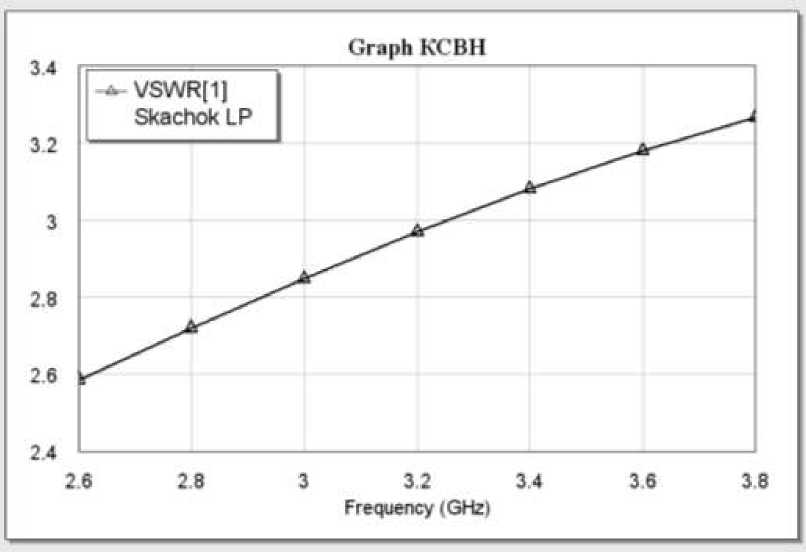
Рис.5. Зависимость КСВН от частоты

Ступенчатый чебышевский переход

Устройство, применяемое для согласования соединения двух линий передачи, называют переходом . Различают плавные переходы, в которых размеры поперечного сечения изменяются плавно, и ступенчатые . Если не наложены ограничения на длину перехода, то может быть достигнуто сколь угодно малое рассогласование в любой полосе частот. Однако на практике желательно, чтобы перехода была минимальной при заданных перепаде волновых сопротивлений, полосе пропускаемых частот и допустимом рассогласовании. Простейшим ступенчатым переходом является четвертьволновый трансформатор, однако он имеет ограниченную широкополостность. Для расширения полосы пропускаемых частот при одновременном улучшении качества согласования применяют многоступенчатые трансформаторы. Длину ступенек – регулярных участков перехода – выбирают одинаковой, и необходимая форма частотной характеристики согласования обеспечивается выбором волновых сопротивлений ступенек [1,2,3,4].

Наибольшее распространение получили переходы с чебышевскими и максимально плоскими частотными характеристиками коэффициента отражения. Первые рассчитываются с помощью полиномов Чебышева и имеют оптимальное соотношение между полосой согласования, допуском на рассогласование и длиной перехода. Переходы с максимально плоскими характеристиками не имеют осцилляций коэффициента отражения в полосе согласования; их фазочастотные характеристики коэффициента передачи ближе к линейным.

Рассмотрим порядок расчета чебышевского трехступенчатого перехода . Возможны два метода расчета: приближенный – метод неопределенных коэффициентов, применяемый в случае малого числа ступенек, и строгий метод – более трудоемкий, но позволяющий рассчитывать переходы с любым числом ступенек. Воспользуемся первым методом. Будем стремится к следующей частотной зависимости коэффициента отражения:

&s = γ T ( tx ) , x = cos θ , (9)

где y - положительный коэффициент, определяющий допуск на рассогласование; t - масштабный множитель, зависящий от заданной полосы пропускаемых частот; θ = 2 π l λ - электрическая длина ступеньки.

Схема замещения ступенчатого перехода показана на рис.6. Волновые сопротивления подводящих линий обозначены через z и z , волновые сопротивления ступенек – через z , z ,z .

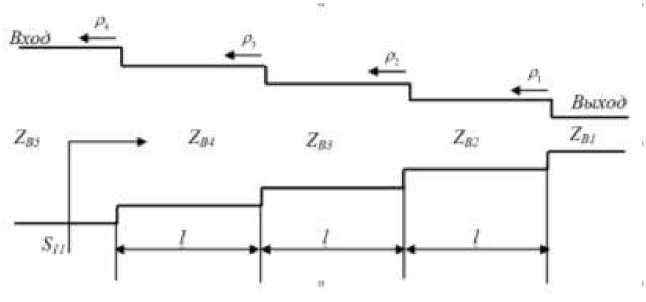
Рис. 6 Схема трехступенчатого чебышевского перехода

На каждом стыке двух линий передачи возникает движущаяся влево отраженная волна, характеризуемая парциальным коэффициентом отражения p = ( zBi - zBi.+1)/(zBi + zBi+1) .

Предположим, что перепады волновых сопротивлений в местах стыка невелики; тогда можно приближенно записать p = zBi- zBi+l = -^z „ 1 ^{lnzB } = 1p-..           (10)

z Bi ⁺ z Bi + 1    ² z Bcp   ^{2              2}    z Bi + 1

Вследствие малости парциальных коэффициентов отражения можно воспользоваться так называемой теорией первого приближения , согласно которой предполагают, что волна, отраженная от каждого стыка, не претерпевает изменений при прохождении остальных стыков. Общий коэффициент отражения ступенчатого перехода при таком предположении равен сумме парциальных коэффициентов отражения от отдельных стыков, пересчитанных в начало перехода:

^ 1 = P 4 ⁺ Р з e — j^{2 6 +} P 2 e — j^{4 6 +} P 1 e — j^{6 6} .

Можно показать, что чебышевской характеристике (6) соответствует симметричное относительно середины перехода распределение коэффициентов отражения. Поэтому p = p и p = p и тогда оказывается

<^ ! = 2 [ p cos 3 6 + p cos 6 ] e ^{- j 3 6} .

Полагая x = cos 6 и учитывая известные представления полиномов

Чебышева

T(x) = x = cos( arcos( x)) = cos 6 ,

T3(x) = 4x3 - 3x = cos(3arccosx) = cos36, запишем модуль коэффициента отражения на входе перехода в виде

|11^(x)| = 21P1T3 ^(x) + P2T1^(x)| = ²|^{4 x 3 - 3}P1^x + P2 ^x| .           00)

Приравнивая выражения (9) и (10), получаем

Y ( 4 x ³ t ³ - 3 xt ) = 2 ^ 4 p x ³ - (3 p - p₂ )x ^

и далее, приравнивая коэффициенты при одинаковых степенях x , получим требуемые значения парциальных коэффициентов отражения:

P 1 = Y t ³ ,   P 2 =

.

Задавать независимо коэффициент Y и масштабный множитель t при проектировании ступенчатого перехода нельзя. Действительно, если с учетом (3.2)подсчитать сумму модулей коэффициентов отражения от отдельных стыков, то, принимая во внимание (3.4), при x = 1 получим

4         1 z

Z Pi= ln = 2 (P1 + P2 ) = YT3 (t) , i=1       2   zB 5

откуда следует, что Y и t связаны между собой:

Y =

^ln ⁽ z В 1/ z В 5 )

2 T 3 ( t)

Масштабный множитель t определяется только заданной полосой согласования

2Асо_с = ^ - ^.                       (13)

Действительно, на границах полосы согласования в соответствии с (9) должны выполняться условия tcos6 =-1,  tcos6 = 1,                   (14)

где У = ю^^ф и У = toIV . Рассмотрев полученное с помощью (14)

выражение

y + y

У - У cos ^{2   1} = 0,

<у₀ = ( to + to )/2 множитель

cos y + cos y = 2 cos —   ²

12    ₂

Нетрудно найти, что на средней частоте cos [(У + У) / 2] должен обращаться в нуль, откуда следует, что длина каждой ступени должна быть равной В . Из условий (3.6) также следует соотношение cos У - cos y = 2 sin

У - У . У + y

^{2     1} sin ^{1     2}

позволяющее найти масштабный коэффициент по заданной полосе согласования:

t =

sin

' п 2 Ato

< 4  too  ,

Проектирование и расчет перехода был проведен в программе «Maxima». Исходными данными для расчета являлись волновые сопротивления z В1 = 50 Ом, z В5 = 26.6 Ом. Материалом для подложки служит ФЛАН - 7.2 толщиной h = 1 мм и с ^. = 7.2. Центральная частота f₀ = 3.2 ГГц , полоса пропускания 2 Af_c =0.5 ГГц. Результаты расчета приведены на рис. 7

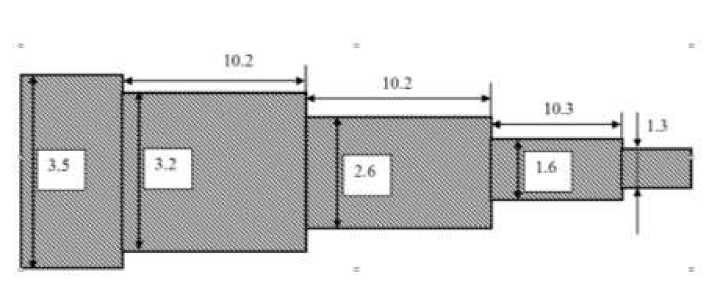
Рис. 7. Чебышевский переход с размерами ступенек

Рассчитанный переход был спроектирован в среде Microwave Studio, внешний вид перехода показан на рис. 8. КСВН перехода представлен на рис. 9.

Рис. 8. Топология чебышевского ступенчатого перехода на МПЛ с плоскостями разгерметизации.

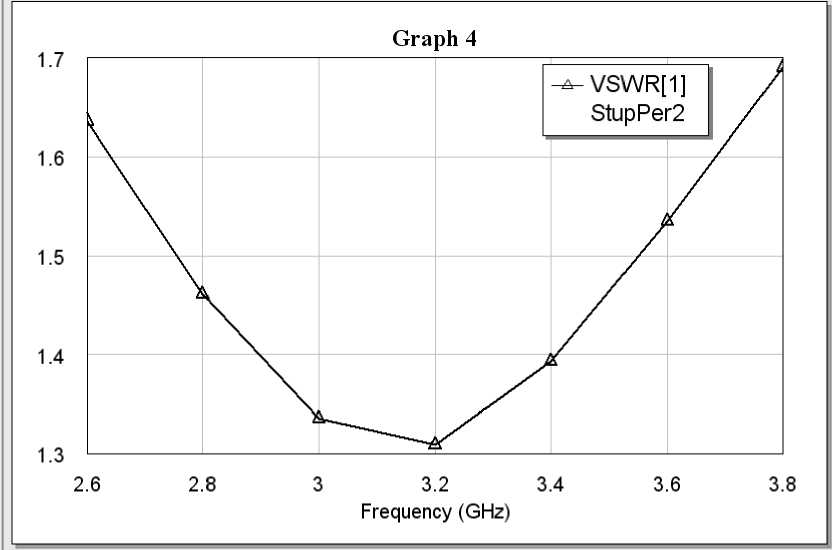
Рис. 9. Зависимость КСВН от частоты

Таким образом, рассчитаны полосковые переходы, составлены программы расчета их параметров в среде «Maxima», составлены программы моделирования переходов в среде «Microwave office», которые подтверждают адекватность расчета.

Полученные результаты можно использовать при расчете различны переходов и в учебном процессе.