Расчет импульсного электромагнитного поля в проводящей среде

В настоящее время во многих областях науки и техники используются импульсные электромагнитные поля [1, 2]. В частности, в задачах воздействия мощных наносекундных электромагнитных импульсов на расплавы металлов используют однополярные импульсы наносекундной длительности без высокочастотного заполнения. Одним из ключевых параметров этого процесса является глубина проникновения импульсного поля внутрь металла. Для синусоидальных колебаний этот параметр называют глубиной скин-слоя.

Возможно, лучшее решение этой задачи приведено в работе [3], где на основе уравнений Максвелла в строгой постановке рассмотрена задача расчета синусоидального электромагнитного поля в проводящем полупространстве. Один из способов использования этих результатов в нашей работе состоит в разложении импульсных полей в ряд Фурье и расчете поля для каждой гармонической составляющей. Однако в связи с малой длительностью используемых импульсов потребуется учитывать большое число гармоник, что значительно усложняет расчеты.

В данной работе используется другой метод. Возбуждение электромагнитных импульсов в проводящей среде с использованием временного подхода рассмотрено в работе [4]. Некоторые вопросы расчетов во временной области приведены в работе [5].

Будем считать, что металл представляет собой сплошную стационарную среду с конечной удельной электрической проводимостью σэ. Из уравнений для векторного потенциала получим волновое уравнение для напряженности электрического поля E:

*                                     *               *

□ : e = и² 1- Ц-j - ^ j +

Vd

—t eε

+---- ε

'. + gradje 8 divj (t‘)dt‘-rotjм

• □   d 2    2 . ^f °³ ° м 1 d

• □u - u ^{a +} —+ — k ⁺

dt2          V 8    ^ J dt эм

σσ

, εμ

* *

где E = E(— t) - вектор напряженности электриче ского поля; * - радиус-вектор в точку наблюде-**

ния; t - временная координата; j = j(r, t ) - объем

-----* -----* м 'М /— ная плотность электрического тока; j = j (r, t) - объемная плотность магнитного тока; и = 1/ ^/8ц - скорость распространения электромагнитных полей в среде.

Аналогично [3] рассмотрим случай, когда электромагнитное поле в рассматриваемой среде создано источниками электромагнитного поля, находящимися вне данной среды. С учетом того, что в проводнике электрического тока удельная магнитная проницаемость равна нулю, получим следующее волновое уравнение для напряженности электрического поля:

• ^{2 —      —} о^{э —}

E - u ² AE + — • — E = 0.

St2

Или в традиционной форме:

• —     52 —

AE -ец —-E -цс э —E = 0 .

Ес л и в ка че с т в е пров од ни к ов эл е ктр иче с кого тока в з я ть м е дь, ал юмин и й, с е ре бро, у которых у дел ь н а я эл е к триче с кая п ров одим ос ть порядка 10⁷ С м/м , то в торое с л а га е мое в ура в нени и на мно го п орядков м е нь ше, че м т ре тье с л а га е м ое . Физ и ч е с ки это оз на ча ет, что в э ти х пров од ни ка х ток и см е ще ния по в еличи не не соиз м е рим о м е ньше то ков пров одим ос т и. Поэ т ому в олн ов ое ура вне н ие редуцируется к параболическому уравне н ию, оп и сыв а юще му д ифф у з ион ные проце с с ы: ^         ^

∆ E - µσ ^э E = 0 .

∂ t

В на ше м с луча е под дейс т вие м эл е к триче с ко го п оля в пров од яще й с ре д е в оз н ика ю т токи пр о в одим ос ти. С ог л асно опре де л е н ию, ток пров од имости – упорядоче нное дви ж е н ие з аряже н н ы х частиц – эл е ктронов . В тв е рдом те л е из -за различных ме х а н из м ов ра с с е яни я у по рядоче нное д в и ж е н ие э л е ктронов на р уша етс я. По этом у ток пров од имо сти ( сл е дов а тел ь но, и на п ряж е н нос ть эл ектр ич е ского п ол я) б у д е т у быв а ть п о м е ре пр оник нов е н ия вглубь твердого тела.

Параболиче с кое у ра вне н ие х орошо изучено, получены анал и тиче ские ре ше ния д л я ча стны х конкре тн ых пра кт иче с к их с лу ча е в . О днако д л я мн огом ерн ы х з а да ч и л и д л я не ста ц иона р ных и не линей ных за да ч ре ше н ия не обх од им о получать численными методами.

Следуя работе [6], рассчитаем пространственно-временные изменения электромагнитного поля в глубине хорошего проводника электрического тока, возбуждаемого на границе твердого тела сторонней напряженностью электрического поля. Рассмотрим двумерную задачу. Электрическое поле имеет только одну составляющую Ez, изме- няющуюся в координатной плоскости xy декартовой системы координат. В качестве импульсных сигналов возьмем прямоугольный видеоимпульс и видеоимпульс в виде полупериода синусоиды в квадрате.

В методе конечных разностей производные по координатным направлениям и времени заменяются разностными. Первые производные по времени заменяются простейшими разностными отношениями, составленными на основе так называемых «разностей вперед». Малые интервалы времени ∆ t выбираются в определенных соотношениях с малыми интервалами расстояния a , равными стороне ячейки сетки в двумерных задачах. Согласно работе [6], стабильность численного решения достигается при выборе интервала по времени из условия: µσ ^э

∆ t <       a ² .

Примем соотношение:

µσ ^э ∆ t =       a ² .

Предположим, что на плоской поверхности массивного электрического проводника возбужден прямоугольный импульс напряженности электрического поля амплитудой 1000 В/м и длительностью τ И =10^–3 с. В качестве проводника электрического тока возьмем медь. Удельная проводимость меди σ =5,6·10⁷ См/м. Длительность видеоимпульса определяется по нулевому уровню. Рассмотрим проникновение электромагнитного поля в глубину проводника, выбрав интервал времени Δ t = 10^–4 с. Интервал расстояния оказался равным a = 2,384·10^–3 м.

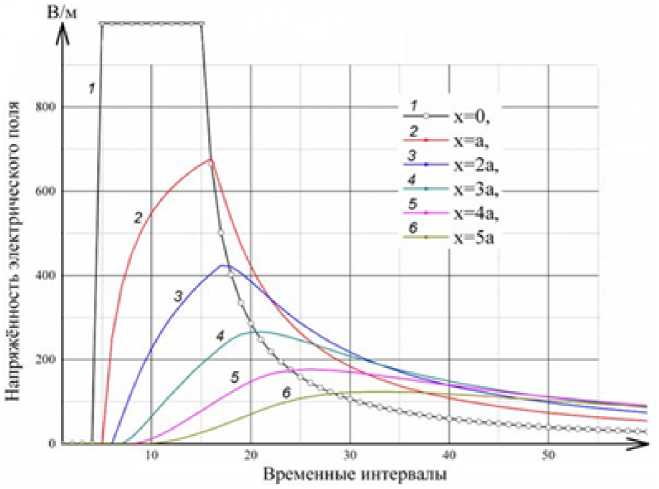
Рис. 1. Напряженность электрического поля прямоугольного импульса внутри проводника в зависимости от временных интервалов

Теплоэнергетика

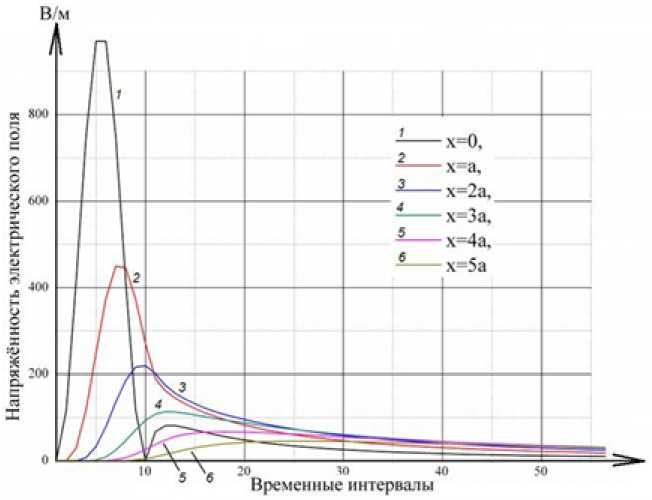
Рис. 2. Напряженность электрического поля синусоидального импульса внутри проводника в зависимости от временных интервалов

Глубина проникновения электрического поля в проводник

τ И , с	Δ t , с	a , мкм	Глубина проникновения ЭМП в проводник, мкм
			Рис. 1	Рис. 2
10 –3	10 –4	2,384·103	5722	3576
10–6	10–7	75,39	181	113
10–9	10 –10	2,384	5,7	3,6
10 –12	10 –13	0,07539	0,18	0,11

Результаты численных расчетов представлены на рис. 1, 2. На рис. 1 показано изменение величины напряженности электрического поля во времени на поверхности проводника x =0 и на глубинах x = a , x = 2 a , x = 3 a , x = 4 a и x = 5 a .

На рис. 2 приведены аналогичные результаты для импульсного сигнала в виде полупериода синусоиды в квадрате с такой же длительностью и амплитудой. На графиках хорошо видно изменение распределения электрического поля как во времени, так и по мере проникновения электромагнитного поля вглубь проводника.

В таблице приведены интервалы времени и пространственные интервалы для других длительностей импульсов от одной миллисекунды до одной пикосекунды. В таблице также приведена оценочная величина глубины проникновения электрического поля в проводник. По классическому определению под глубиной проникновения электрического поля в проводник принимается такое расстояние от поверхности твердого тела, на котором максимальная величина электрического поля уменьшается в e раз (примерно в 2,718 раз).

Результаты численных расчетов свидетельствуют о том, что проникновение электромагнитного поля в проводник обусловлено диффузионными процессами. Глубина проникновения электрического поля уменьшается с уменьшением длительности видеоимпульса и зависит от величины энергии электромагнитного поля в импульсном сигнале.