Расчет инструмента для волочения квадратных профилей и труб

Волжский филиал Института металлургии и материаловедения им. А.А. Байкова РАН, г. Самара

Показано применение метода конформных отображений и теории упругости плосконапряженных тел для определения напряженного состояния волок, используемых для производства квадратных профилей и труб.

Одним из экономичных видов металлоконструкций являются квадратные профили и трубы высокой точности [1]. Для их производства широко используется процесс волочения в фасонные волоки, особенно для завершающих операций доводки и калибровки [2].

Волоки являются важнейшим инструментом, формообразующим наружную поверхность профилей и труб. Выход волок из строя - одна из основных причин нарушения процесса волочения, поэтому разработка методики расчета волок, обеспечение их максимальной прочности имеет важное значение. Применявшийся ранее метод расчета фасонных волок на прочность, основанный на использовании формулы Ляме, не дает необходимой степени точности [2].

В данной работе при расчете поля напряжений в волоке давление от деформируемого металла в полости квадратного отверстия по длине и по сечению принимаем постоянным, рис.1. Это дает возможность ис пользовать методы конформных отображений и теории упругости плосконапряженных тел [3]. Согласно методу Д.И. Шермана [4], поставленная задача для двухсвязной области S, являющейся поперечным сечением фасонной волоки, может быть сведена к задаче для односвязной области. Такой подход использован при расчете на прочность контейнеров для плоских слитков [5].

Отобразим внешность квадратного контура L 1 на внешность единичного круга (рис.1). Функцию, осуществляющую конформно это соответствие, задаем приближенно в виде

Z = у(л)= af X + - + c ^ ( XX )’ где a, b, c — коэффициенты, подлежащие определению из условий достаточно хорошего соответствия контура внутренней полости волоки и отображения единичного круга. Этого можно добиться соответствующим подбором трех совпадающих точек А1, А2, А3

Рис. 1. Схема к расчету напряженного состояния волоки

и А" , , А"₂, А"₃.

Компоненты тензора напряжений o x , o y , т xy в произвольной точке фасонной волоки с наружным радиусом R определяются системой трех уравнений [5].

^O x ^{+ O} y = ^4Re ^Ф ( ^Z )

- O x + O y = 2Re [ Z Ф' ( Z ) + F ( Z ) ]

T xy = Jm [ Z Ф' ( Z ) + F ( Z ) ]

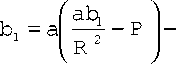
R

4a1

2b a2

a2

3—- ( bb_L + b₃ )

R 2     1    3

где

ф ( z ) = ^^L^в + 3 A Z ²;

X Ц) R R

ф' ( z ) =

ф '^(Л)х W- ф (Mx 'U ¹ [ x Ш

+ 6 в з V>

R

a4

3R4

a1

a2

—- ( bb + b₃ ) ( b₃ + 2bc + 2bc - 3b ) +

R2

+ a_Lb ( 1 + c ) + 3a₃c

^а 1

а ₃

в 1

aa1

; R

a3

= — ( a l b ^{+ a} 3 );

R 31   3

1a

-

2R

b 1 ;

f ( z ) = ZA а - з а

' ' Х '( Л ) R ³

Z ²

R ³

-

6 вх .

R

^в 3 = — ^-^r ( bb L ⁺ b 3 ) ^;

3 R R 313

В записанных уравнениях Re - действительная часть, Jm - мнимая часть, ф ( Z ), у ( Z ) -аналитические регулярные функции комплексной переменной Z=x+iy внутри области S. Эти функции целесообразно взять в виде ряда

b3

= ^y c 4a i ^{- 3}^y ^{( b}b i + b 3 )

R

R

a

R

a

a2

— (bb_L + b₃ ) [1 + 3 ( 2c + 2bc² + b² )]■

+

ф ( Л ) = A + Л ,

^ ( Л ) = b 1 + b- .

Л Л ³

Коэффициенты a 1 , a ₃, b_x, b ₃, а 1 , а ₃, 3 1 , в ₃ находятся из следующих выражений:

+ a_L ( 1 + b² ) + 3a₃b ( 1 + c ) + a_Lc ( 3c + b )

Расчет предельного состояния по третьей теории прочности позволяет определить наиболее нагруженные участки фасонной волоки и выбрать ее размеры.

о =0-0 <Ы = °^, экв y x L J ,

^K 3

a

1 - c

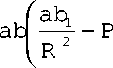
1+

/

2 a²

R2

4a1

-

3~ ( bb + b 3 )

-

-

a

R

a1

-

— (bb_L ⁺ b 3 ) X

R

х ( зь² + 2c² + b²c + c + 1 )

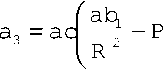
1 /

-

4 a⁴

R

- a1

-aT ( ^bb L ^{+ b} 3 ) ( ^12bc

R

+ b +

3b );

где o _T - предел текучести материала волоки; Кз - коэффициент запаса, Кз=1,5.

В качестве примера рассмотрим расчет напряженного состояния фасонной волоки с наружным радиусом R=30мм, используемой для калибровки волочением квадратного прутка с размерами 20 x 20 мм и закругленными углами радиусом 2 мм. Отображающая функция имеет вид

Z = х ( Л ) = 12 1 Л -

0,167 "| л ³ J

Эпюра напряжений приведена на рис.2. Для сравнения на этом же рисунке показаны результаты расчета напряжений, вычисленных по формуле Ляме

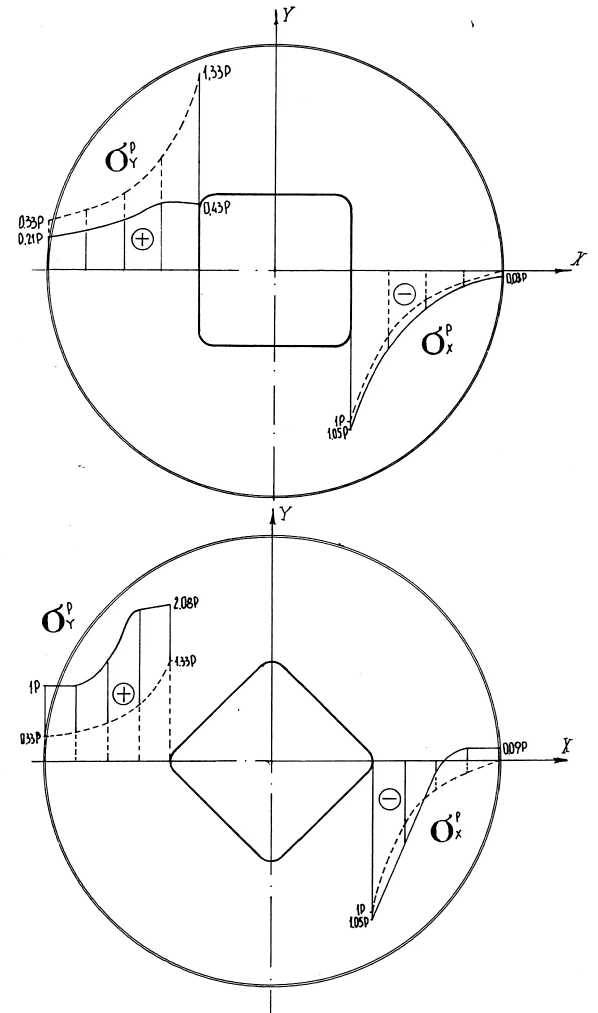
Рис. 2. Поле напряжений.

- квадратное отверстие, ____- круглое отверстие

° У =

Pr2

R ² - r ²

R ²

¹ + Р

°

Pr2

x

R ² - r^г

Г

¹ —

V

R ²

р ²

где r - радиус круглого отверстия, равного по площади квадратному отверстию.

Из анализа эпюр распределения напряжений по толщине стенки волоки в наиболее характерных сечениях видно, что форма отверстия существенно изменяет характер напряжений в радиальном и окружном направлениях. Наиболее опасная с точки зрения разрушения концентрация напряжений имеет место вблизи углов квадратного контура.

Таким образом, изложенное показывает обоснованность расчета фасонных волок на прочность по методике, основанной на решении плоской задачи теории упругости в напряжениях и конформных отображений.