Расчет из первых принципов оптимальной толщины поглотителя в мёссбауэровской спектроскопии

Во всех спектроскопических методах анализа вещества важнейшим параметром является качество экспериментального спектра SNR, которое определяется отношением амплитуды сигнала S к величине шума N . На практике всегда стремятся получить максимальное значение этого параметра. Существует два способа повышения качества экспериментального спектра. Первый заключается в увеличении времени проведения измерений, т. к. сигнал линейно растет со временем t , а шум — как корень квадратный из t . Второй заключается в увеличении концентрации анализируемого вещества, что приводит к росту амплитуды сигнала. Первый путь приводит к тому, что время эксперимента будет стремиться к бесконечности. Недостаток второго пути заключается в том, что при увеличении концентрации вещества начинают сказываться эффекты насыщения, которые приводят к искажению формы спектральных линий, и возрастает вклад нерезонансного поглощения излучения. Все это затрудняет дальнейшую математическую обработку экспериментальных спектров, направленную на получение достоверной качественной и количественной информации об исследуемом веществе.

В случае мёссбауэровской спектроскопии в геометрии на пропускание излучения регистрация мёссбауэровского спектра может занимать от нескольких часов до нескольких дней. Причинами этого могут быть: низкая концентрация резонансных ядер; малое значение величины фактора Лэмба—Мессбауэра f, определяющего величину экспериментально наблюдаемого резонансного эф- фекта ε, а также влияние матричных эффектов, которые зависят от входящих в состав образца элементов, с большим коэффициентом электронного поглощения. В этом случае для получения спектра с необходимым качеством может потребоваться продолжительный период времени. Таким образом, выбор оптимальных условий эксперимента имеет принципиальное значение, т. к. позволит получить заданное качество спектра за минимальное время.

В мёссбауэровской спектроскопии принято подразумевать под толщиной исследуемого вещества концентрацию содержащегося в нем резонансного изотопа, выраженную в единицах мг/см2. При небольшой толщине поглотителя содержание резонансных ядер будет мало, что приведет к малому значению величины резонансного поглощения и соответственно отношению сигнал/шум. При очень большой толщине поглотителя будет возрастать вклад нерезонансного поглощения излучения, что также приведет к уменьшению отношения сигнал/шум. Таким образом, существует некоторая оптимальная толщина поглотителя, при которой качество спектра в заданных условиях будет максимально.

В ряде работ [1–4] приводятся методы оценки и расчета значений оптимальных толщин, где даются более или менее простые аналитические выражения. Их общим ограничением можно считать использование различных приближений для оценки значений интеграла пропускания. Так, в [1, 2] при модельных расчетах не учитывается влияние толщины поглотителя на уширение спектральных линий, что приводит к завышенным значениям величины эффекта и, следовательно, к за- вышенным оценкам оптимальной толщины; в качестве примерной оценки толщины рекомендуется брать значение 1/µ, где µ — массовый коэффициент нерезонансного ослабления. В работе [3] интеграл пропускания аппроксимируется с помощью функций Бесселя, и рассматриваются его приближения при различных соотношениях ширин спектральных линий источника и поглотителя. Использование предложенных в работе выражений приводит к сильно заниженным значениям толщины поглотителя по сравнению с расчетами, выполненными в [1, 2]. В [4] приводится разработанная авторами программа моделирования различных мёссбауэровских экспериментов на пропускание. Авторы этой работы ограничились рассмотрением случая легкой матрицы (система Al—Fe), что не позволяет проверить корректность работы предлагаемого алгоритма для разных матриц.

Настоящая работа посвящена разработке методики определения оптимальной толщины поглотителя, основанной на прямом вычислении интеграла пропускания.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

В мёссбауэровской спектроскопии отношение сигнал / шум определяется следующим выражением:

SNR =

S

I j - I 0

где величина резонансного эффекта ε = (I∞ – - 10) /I„, шум N = ^J^ , 10 и I„ — количество заре- гистрированных импульсов в резонансе и вне его.

Форма линий испускания источника и поглощения резонансными атомами описывается распределением Лоренца

L ( v ) =

( ^Г /2 ) 2

( v - v 0 ) ² + ( Г /2 ) 2

где: v — текущее значение доплеровской скорости источника (мм/с); v 0 — положение резонансной линии (мм/с); Г — ширина линии на полувысоте (мм/с).

В случае движущегося источника и неподвижного поглотителя интеграл пропускания, определяющий количество зарегистрированных квантов для данной скорости I ( v ), будет иметь следующий вид [5]:

I(v) = KI Sie-^dtot x x (1 -/s) + f J Ls(v'-v)e"La(v’)tef(d)dv' + KIstn. (2) пГ -J

Здесь I S — интенсивность квантов, испущенных мёссбауэровским источником (имп/с); K — вероятность регистрации излучения детектором; µ — массовый коэффициент нерезонансного поглощения излучения (см²/г); d _tot — общая толщина поглотителя, включающая содержание резонансного изотопа и матричных элементов; d — толщина поглотителя по резонансному изотопу (г/см²); f S — фактор Лэмба—Мёссбауэра источника; v — скорость источника (мм/с); η — коэффициент, учитывающий вклад фона, который можно определить из амплитудного спектра источника излучения, прошедшего через исследуемый поглотитель; t — время накопления спектра (с); L S , L a — профили линий испускания и поглощения для источника и поглотителя соответственно; d _eff — безразмерная эффективная толщина поглотителя по резонансному изотопу. Эффективная толщина оп-

N ределяется как d ff(d) = wf n„d —A, где w — сте-eff a 0 M пень обогащения поглотителя резонансным изотопом; fa — фактор Лэмба—Мёссбауэра поглотителя; σ0 — максимальное сечение резонансного поглощения (см2); NA — постоянная Авогадро (моль–1) и M — молярная масса поглотителя (г/моль).

В дальнейшем будем различать экспериментально наблюдаемое в мессбауэровских спектрах (SNR эксп ) и исправленное (SNR исп ) значения отношения сигнал / шум. Заметим, что интенсивность линии ( I ∞ – I 0 ) не зависит от наличия фона. Тогда наблюдаемое значение получается при подстановке в знаменатель соотношения (1) I Jxp — экспериментально наблюдаемая интенсивность вне резонанса. Исправленное значение соответствует гипотетическому отношению сигнал / шум, которое имело бы место в отсутствие фонового излучения; оно получается при замене I Jxp на I „ = (1 -- П ) I Jxp .

ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ

Для проверки полученных в теоретической части результатов, касающихся определения оптимальной толщины поглотителя, были выбраны вещества, мёссбауэровские спектры которых имеют одиночную или дублетную структуру. Такими веществами служили ферроцианид калия K 4 [Fe(CN) 6 ]∙3H 2 O (ЦФК), нитропруссид натрия Na 2 [Fe(CN) 5 NO]∙2H 2 O (НПН) и смесь НПН с сульфатом бария (1:2 по мольной доле). Первые два образца моделируют ситуацию резонансного изотопа в легкой матрице, а третий образец моделирует ситуацию резонансного изотопа в тяжелой матрице. Из данных соединений были приготовлены поглотители, толщина которых варьировалась

Табл. 1. Экспериментальные данные

Поглотитель	Толщина поглотителя, мг/см2	Эффективная толщина d eff	Ширина линии Γ , мм/с	Величина эффекта ε	SNR исп	SNR теор
	5.8	1.14	0.257 ±0.002	0.230 ±0.002	107.8 ±0.7	106.6
	7.0	1.37	0.267 ±0.002	0.276 ±0.002	116.1 ±0.7	109.8
	8.1	1.60	0.270 ±0.002	0.293 ±0.002	116.4 ±0.6	110.4
ЦФК	9.3	1.83	0.277 ±0.002	0.322 ±0.002	110.8 ±0.7	108.9
	10.5	2.05	0.290 ±0.002	0.323 ±0.003	102.9 ±0.7	106.1
	11.6	2.28	0.303 ±0.004	0.318 ±0.004	96.2 ±0.9	102.3
	12.8	2.51	0.307 ±0.004	0.316 ±0.004	90.4 ±1.0	97.9
	9.4	2.22	0.239 ±0.001	0.191 ±0.001	93.9 ±0.3	101.2
	11.2	2.67	0.245 ±0.001	0.231 ±0.001	105.6 ±0.3	106.2
	13.1	3.11	0.249 ±0.001	0.253 ±0.001	110.2 ±0.4	108.6
НПН	15.0	3.55	0.252 ±0.001	0.269 ±0.001	112.4 ±0.5	109.1
	16.9	4.00	0.261 ±0.001	0.274 ±0.001	110.1 ±0.5	108.2
	18.7	4.44	0.270 ±0.002	0.285 ±0.001	106.5 ±0.5	106.2
	20.6	4.89	0.272 ±0.002	0.287 ±0.001	104.2 ±0.5	103.4
	1.8	0.43	0.218 ±0.001	0.064 ±0.001	54.5 ±0.3	55.9
	2.6	0.61	0.236 ±0.001	0.084 ±0.001	63.7 ±0.4	64.9
	3.3	0.78	0.229 ±0.001	0.091 ±0.001	68.2 ±0.5	69.1
НПН +	4.0	0.95	0.237 ±0.005	0.111 ±0.001	72.3 ±0.6	70.1
+ BaSO 4	4.7	1.13	0.234 ±0.004	0.111 ±0.001	70.1 ±0.5	68.7
	5.5	1.30	0.236 ±0.004	0.103 ±0.001	64.0 ±0.5	65.8
	6.2	1.47	0.236 ±0.005	0.114 ±0.001	62.5 ±0.6	61.9

в окрестности расчетных значений оптимальных толщин. Измерения проводились на мёссбауэровском спектрометре СМ 2201. Источником в экспериментах служил радиоактивный изотоп 57Co(Rh) активностью 20 мКи. В качестве детекто- ра излучения использовался пропорциональный счетчик, наполненный газовой смесью (Xe + 10 % CH4). Время накопления мёссбауэровских спектров составило 23 ч для ферроцианида калия и нитропруссида натрия, а для образца с тяжелой матрицей — 72 ч. Накопление амплитудных спектров для всех образцов проводилось в течение 1 ч для получения минимальной статистической ошибки. Все измерения проводились при комнатной температуре.

По методике, описанной в работе [5], из амплитудных спектров каждого образца мы определяли коэффициент η , учитывающий вклад фона, который позволил получить исправленные значения скорости счета вне резонанса и подставить их вместо I ∞ в формулу (1) для определения SNR исп .

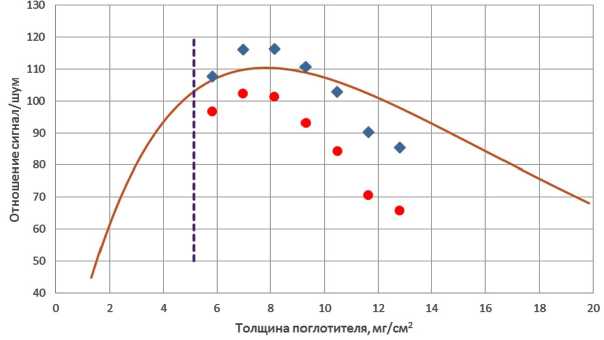
Рис. 1. Зависимость отношения сигнал/шум от толщины поглотителя по резонансному изотопу для ЦФК. Круглыми точками обозначены наблюдаемые значения, квадратными — исправленные. Непрерывная линия соответствует теоретически рассчитанной зависимости для случая отсутствия фона. Пунктиром обозначена граница области приближения тонкого поглотителя

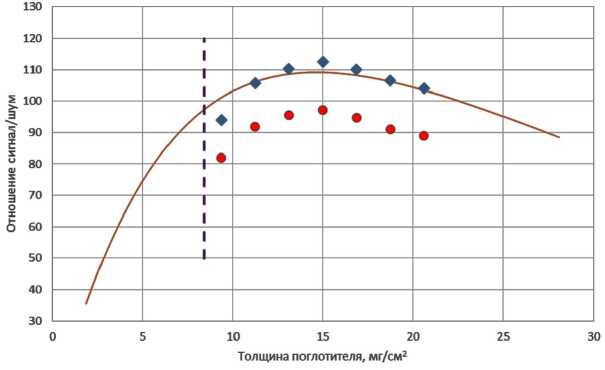
Рис. 2. Зависимость отношения сигнал/шум от толщины поглотителя по резонансному изотопу для НПН. Круглыми точками обозначены наблюдаемые значения, квадратными — исправленные. Непрерывная линия соответствует теоретически рассчитанной зависимости для случая отсутствия фона. Пунктиром обозначена граница области приближения тонкого поглотителя

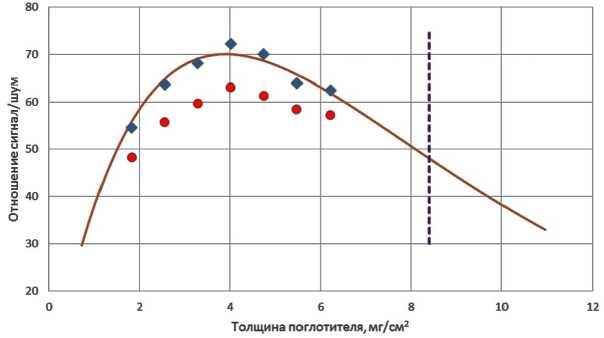
Рис. 3. Зависимость отношения сигнал/шум от толщины поглотителя по резонансному изотопу для НПН + BaSO 4 .

Круглыми точками обозначены наблюдаемые значения, квадратными — исправленные. Непрерывная линия соответствует теоретически рассчитанной зависимости для случая отсутствия фона. Пунктиром обозначена граница области приближения тонкого поглотителя

Полученные в результате математической обработки экспериментальных спектров значения отношения были сопоставлены со значениями SNR теор , рассчитанными по формулам (1–2). Результаты сравнения представлены в табл. 1.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Как видно из табл. 1, экспериментально найденное значение оптимальной толщины, определяемое положением максимума SNR, в пределах ошибки эксперимента совпадает с рассчитанным теоретически: 8 мг/см² для гексацианоферрата(II) калия, 15 мг/см² для нитропруссида натрия и 4 мг/см² для нитропруссида натрия в тяжелой матрице сульфата бария. На рис. 1–3 представлены зависимости экспериментального SNR эксп (нижний ряд точек) и исправленного SNR исп (верхний ряд точек) отношения сигнал/шум от толщины поглотителя.

Из рисунков видно: несмотря на то что зависимости исправленных и наблюдаемых значений SNR от толщины различаются по величине, однако положения их максимумов во всех трех случаях совпадают. Данный результат означает, что при проведении расчетов по определению оптимальной толщины поглотителя можно не учитывать влияние фона. Действительно, проведенное нами моделирование спектров с различными вкладами фона показывает, что наличие фонового излучения незначительно сказывается на величине оптимальной толщины поглотителя.

Следует отметить, что найденные оптимальные толщины для образцов, содержащих изотоп в легкой матрице, лежат выше границы, соответствующей приближению тонкого поглотителя, и характеризуются уширенными спектральными линиями (табл. 1). В мёссбауэровской спектроскопии под тонким поглотителем принимается такая толщина d мин , при которой искажение формы спектральных линий пренебрежимо мало и удовлетворяет условию L ( v 0 ) ·d мин ≤ 1 [6]. В случае тяжелой матрицы (рис. 3) оптимальная толщина поглотителя находится ниже границы, соответствующей тонкому поглотителю.

Сравнение теоретических расчетов с экспериментальными данными показывает, что выбор оптимальной толщины поглотителя сильно зависит от величины нерезонансного поглощения, определяемого влиянием матрицы. На рис. 4 представлен график, демонстрирующий влияние матрицы на зависимость отношения сигнал/шум и положе- ние ее максимума. Видно, что из-за высокого вклада нерезонансного поглощения излучения в тяжелых матрицах значение оптимальной толщины смещается в сторону меньших значений.

Таким образом, при выборе оптимальной толщины следует учитывать границу приближения тонкого поглотителя. В случае если рассчитанная толщина больше, то следует отдать предпочтение максимальной толщине, при которой соблюдается приближение тонкого поглотителя.

В табл. 2 приведено сравнение экспериментальных и расчетных значений оптимальной толщины поглотителя со значениями, полученными по методикам [2, 3], а также максимальные значения (критические) толщин, при которых допустимо приближение тонкого поглотителя. Из таблицы видно, что результаты расчета, полученные с помощью предложенного алгоритма, наиболее близки к экспериментальным значениям по сравнению с [2, 3].

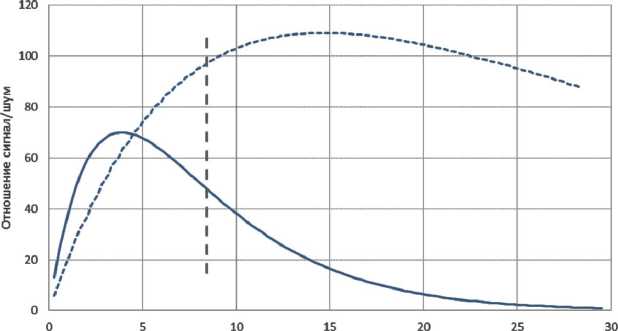
Толщина поглотителя, мг/см2

Рис. 4. Зависимости отношения сигнал/шум от толщины поглотителя по резонансному изотопу для легкой (пунктирная линия) и тяжелой (сплошная линия) матриц.

Вертикальным пунктиром отмечена граница области приближения тонкого поглотителя

Табл. 2. Оптимальные значения толщин для различных поглотителей

Поглотитель	Экспериментальное значение, мг/см2	Рассчитанное значение, мг/см2	Значение по [2], мг/см2	Значение по [3], мг/см2	Критическое значение, мг/см2
ЦФК	8.1	7.9	13.8	6.0	5.1
НПН	15.0	14.6	27.2	7.1	8.4
НПН + BaSO 4	4.0	3.9	2.3	2.9	8.4

ВЫВОДЫ

В настоящей работе предложена методика численного определения оптимальной толщины, которая дает лучшее совпадение с экспериментом по сравнению с имеющимися в литературе подходами.

В ходе исследования был сделан вывод, что прибегать к предварительному расчету оптимальной толщины наиболее целесообразно в случае тяжелых матриц и низких концентраций резонансных атомов или малых значений фактора Лэмба—Мёссбауэра. В противном случае значение оптимальной толщины может оказаться вне приближения тонкого поглотителя, и выбор такой толщины приведет к искажению формы (уширению) спектральных линий. Показано, что наличие фонового излучения не влияет на положение максимума SNR, которое соответствует значению оптимальной толщины, а только приводит к увеличению времени набора экспериментального спектра для достижения заданного качества.

Наиболее важное значение полученные результаты имеют в случае многофазных систем, в которых атомы с резонансными ядрами находятся в различных локальных окружениях, соответствующих синглетам, дублетам и секстетам. В этих случаях оптимальную толщину поглотителя следует выбирать по наиболее интенсивному сигналу в спектре.