Расчет изохорной теплоемкости аргона от газовой до твердой фазы методом молекулярной динамики

Герман Е. И., Цыдыпов Ш. Б., Емельянов Г. В. Расчет изохорной теплоемкости аргона от газовой до твердой фазы методом молекулярной динамики // Вестник Бурятского государственного университета. Химия. Физика. 2025. Вып. 4. С. 14–19.

Методы численного эксперимента динамического типа (методы молекулярной динамики и Монте-Карло) в классических системах частиц позволяют отслеживать микросостояния системы (координаты, скорости, ускорения отдельных частиц), суммирование и усреднение по времени которых отражают основные макроскопические параметры — давление, плотность и температуру. Знание о взаимозависимости последних макроскопических величин позволяет рассчитать в ходе численного эксперимента основные термодинамические параметры испытуемых систем в различных фазовых состояниях [1].

В данной работе в качестве объекта исследования методом молекулярной динамики выбран аргон как вещество с простым сферически симметричным потенциалом взаимодействия его атомов, требующее вычислительного времени гораздо меньше, чем вещества с более сложным взаимодействием его частиц. С другой стороны, аргон широко используется в энергетике и технике для создания защитной теплоизоляции как инертный газ с низкой теплопроводностью, не вступающий в химические реакции даже при высоких температурах. Исследование взаимозависимости давления, плотности и температуры, т. е. термического уравнения состояния, а также их связь с энергетическими величинами легче отслеживать на моделях простых веществ, таких как инертные газы.

В качестве теплоизоляции инертные газы могут находиться в условиях с постоянным объемом. Поэтому представляется интересным проследить температурную зависимость изохорной теплоемкости аргона от газовой до твердых фаз при различных давлениях.

Из-за ограниченных по скорости вычислений и возможностей современных компьютеров численными методами исследуются системы, состоящие из числа частиц порядка 103. Это число частиц во много раз меньше, чем в моле вещества в реальных теплофизических экспериментах. По этой причине в этих системах отсутствуют флуктуации плотности частиц, импульса и других величин. Эти недостатки успешно преодолеваются в методе молекулярной динамики использования периодических граничных условий для того, чтобы ограниченное вычислительной мощностью число частиц порядка 103 достаточно точно отражало поведение всей большой системы в равновесных состояниях.

Классическая молекулярная динамика позволяет моделировать микроканони-ческий ансамбль системы с постоянными значениями объема V, числа частиц N и энергии E. В процессе моделирования такой системы можно наблюдать и фиксировать флуктуации температуры. По этим данным можно вычислить средний квадрат температуры 2>, а также квадрат средней температуры ² и найти теплоемкость системы при постоянном объеме С V с помощью следующего выражения [2]:

<    T2 > - < T >2 3 Л 3kNл = 1 , <    T >2 2N [ 2CV ;

здесь k — постоянная Больцмана.

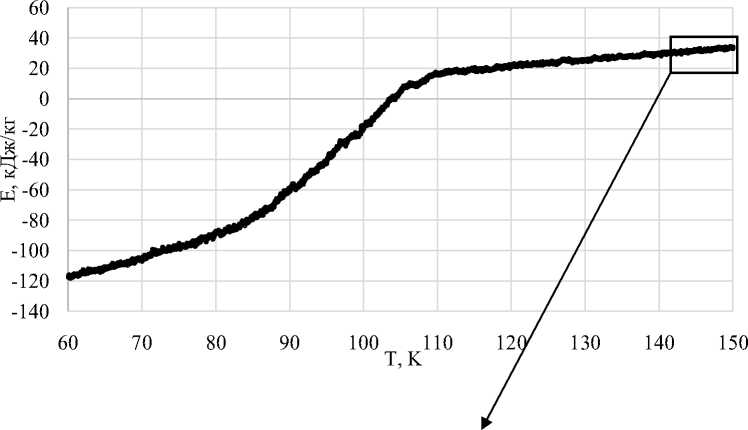
Алгоритм классической молекулярной динамики достаточно легко модифицировать для моделирования процессов изохорного охлаждения или нагрева [2], что позволило нам в процессе численного моделирования получать изохоры внутренней энергии системы частиц аргона Е от газовой до твердой фазы (рис. 1). Справа приведен участок графика в увеличенном виде с линией тренда, полученной методом наименьших квадратов и уравнением этой линии, где угловой коэффициент 0,4114 равен С V = dE/dT .

По полученной температурной зависимости внутренней энергии системы частиц аргона (рис. 1) вычислялась его теплоемкость С_V :

c=|-1

V 1st)r

.

Значение теплоемкости согласно выражению (2) определялось как тангенс угла наклона отрезков прямой на дискретных участках изменения температуры в 5 К. Для вычисления углового коэффициента для каждого отрезка производилась линейная аппроксимация зависимости E от T методом наименьших квадратов. Значение теплоемкости для каждого отрезка прямой определялось как его угловой коэффициент и относилось к средней на отрезке температуре (рис. 1).

33,5

32,5

~й 31,5

W 30,5

29,5

y = 0,411x - 27,94

144         145         146

Т, К

147         148

Рис. 1. Зависимость внутренней энергии аргона от температуры, полученная при моделировании методом молекулярной динамики [2] при плотности 109,4 кг/м3 и скорости охлаждения 109 К/с

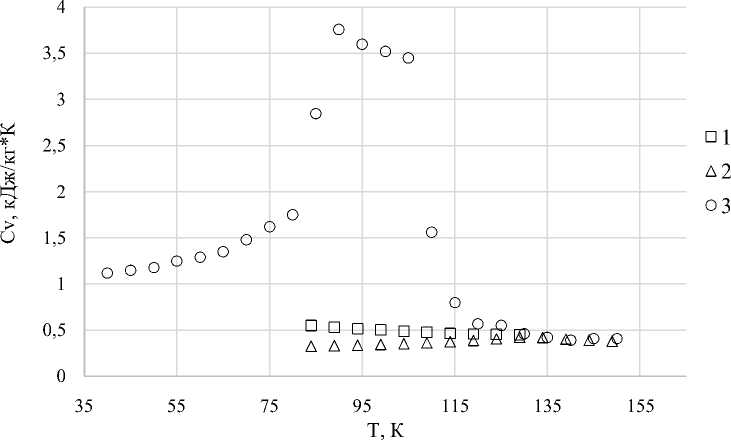
Рис. 2. Температурная зависимость изохорной теплоемкости С V аргона при охлаждении со скоростью 10⁹ К/с и плотности 109,4 кг/м³: 1 — в жидком состоянии [3]; 2 — в газообразном состоянии [3]; 3 — данные наших численных расчетов

Так, например, на правой части рисунка 1 приведена увеличенная часть графика в интервале температур Т от 142 до 148 К и внутренней энергии Е от 29 до 33,5 кДж/кг. Из уравнения отрезка прямой линии тренда, приведенного на этом рисунке 2, видно, что теплоемкость C V аргона в данных условиях равна 0,4114 кДж/(кг·К), что превышает теплоемкость аргона как одноатомного идеального газа при нормальных условиях, равную 0,3122 кДж/(кг·К), на 0,0992. При нормальных условиях (0 °C и 101325 Па) плотность аргона равна 1,7839 кг/м³.

Результаты наших расчетов изохорной теплоемкости аргона при охлаждении со скоростью 109 К/с приведены на рисунке 2 (плотность 109,4 кг/м3, при температуре 150 К давление в системе равно 4 МПа).

Как видно из рисунков 1 и 2, при охлаждении системы частиц аргона наблюдаются характерные скачки в динамике теплоемкости, соответствующие фазовым переходам газ — жидкость и жидкость — твердое тело. На участке от 150 до 110 К наблюдается зависимость, соответствующая газовой фазе аргона, а на участке от 110 до 85 К теплоемкость испытывает скачок, что свойственно фазовому переходу. В данном случае это состояние интерпретируется нами как двухфазная область «перенасыщенный пар + жидкость». Ниже 85 К аргон переходит в твердую фазу. На кривой температурной зависимости теплоемкости С V аргона в твердой фазе наблюдается заметное уменьшение углового коэффициента dC_V / dT с уменьшением температуры.

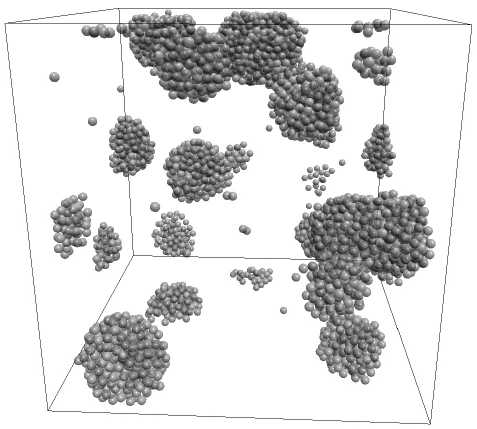
Рис. 3. Конфигурация частиц аргона, образованная при изохорном охлаждении со скоростью 109 К/с

По-видимому, этот факт связан с образованием (рис. 3) кластеров частиц аргона с пустотами относительно больших размеров по сравнению с межатомными расстояниями [4]. Это образование кластеров обусловлено тем, что увеличение плотности твердого аргона, вызванное понижением температуры и соответственно уменьшением межатомных расстояний при неизменном объеме предоставленного системе частиц, приводит к образованию значительных пустот [5], как показано на рисунке 3.