Расчет эйконала светового поля для заданного масштабирования распределения освещенности

Задача расчета оптических элементов для преобразования и фокусировки светового пучка в заданную область является актуальной для широкого круга прикладных задач, включающего задачи светотехники и лазерной оптики. Задача расчета оптического элемента состоит в расчете формы оптической поверхности элемента из условия выполнения заданного преобразования входного освещающего пучка.

Ряд методов решения задач данного класса в приближении геометрической оптики разработан для дифракционных оптических элементов [1-6]. В этом случае задача ставится как задача расчета эйконала светового поля в некоторой плоскости из условия выполнения заданного преобразования координат или фокусировки в требуемую область в плоскости, отстоящей от исходной плоскости на заданном расстоянии. При этом форма поверхности дифракционного элемента может быть однозначно восстановлена по распределению эйконала в плоскости.

В общем случае задача расчета эйконала из условия фокусировки в заданную двумерную область сводится к решению нелинейного дифференциального уравнения второго порядка в частных производных, известного как уравнение Монже-Ампера. Аналитическое решение данного уравнения возможно только для тривиальных задач, обла- дающих радиальной или цилиндрической симметрией [1].

В данной работе в приближении геометрической оптики рассмотрен численный метод нахождения функции эйконала, обеспечивающей в заданной плоскости различное масштабирование по осям координат входного распределения освещенности. Метод разработан для случая непараксиального приближения и основан на представлении функции эйконала в виде системы бикубических сплайнов. Параметры сплайнов определяются с использованием метода оптимизации из условия реализации заданного преобразования координат.

Постановка задачи

Требуется найти для произвольных коэффициентов масштабирования по осям k ₁ и к 2 функцию эйконала Т ( u , v ) , определенную в плоскости z = 0 и обеспечивающую масштабирование распределения освещенности в выходной плоскости z = f . В этом случае, требуемое лучевое преобразование координат имеет вид

x ( u , v ) = к 1 и

y ( и , v ) = к 2 v ,

где (и, v) - координаты точки выхода луча в плоскости z = 0, а (x, у) - координаты точки прихода этого луча в выходную плоскость z = f. Так как якобиан преобразования (1) равен константе, то эйконал, реализующий преобразование (1), обеспечит формирование области с распределением освещенности такого же вида, как и в плоскости z = 0, но с измененным масштабом.

Приведенная постановка задачи включает расчет дифракционных оптических элементов. Действительно, при условии выполнения приближения тонкого оптического элемента, высота дифракционного микрорельефа пропорциональна функции эйконала, взятой по модулю λ , где λ – длина волны [1-3]. Отметим также, что по функции эйконала и по волновому фронту освещающего пучка может быть восстановлена недифракционная преломляющая или отражающая поверхность оптического элемента, обеспечивающая заданное масштабирование (1).

Координаты оптического луча в выходной плоскости зависят от функции эйконала следующим образом [1-3]:

f

x ( и , v ) = u + * и

у ( и , v ) = v + * v

V i-(*и )2-го2 ’ f.

V i-(* )2-(*v )2'

Метод решения

В силу симметрии задачи достаточно найти эйконал в первом квадранте. Функцию эйконала предлагается представить в виде системы бикубических сплайнов на прямоугольной сетке (рис. 1).

Бикубические сплайны сохраняют непрерывность функции, ее первых и смешанной производных на границах, поэтому преломляющая или отражающая поверхность, восстановленная по такой функции эйконала, будет также непрерывной. Для определения параметров сплайна необходимо задать значения функции, а также ее первых и смешанной производных в углах прямоугольной области определения сплайна.

Так как известны зависимости x = x ( и , v ) , у = у ( и , v ) , то первые производные эйконала выражаются из (2) следующим образом:

*‘ = u

* v =

x ( и , v ) - и

Jfг + (x (и, v)- и )2 + (у (и, v)- v )2

у (и, v)-v f2 +(x (и, v)-и )2 +(у (и, v)-v )2

Таким образом, неизвестными остаются значения функции эйконала и значения сме-

Av

В случае, когда коэффициенты масштабирования равны ( k₁ = k ₂ = k ), несложно получить точное аналитическое решение:

* ( и , v )

k - 1

V ( k ^- 1 ) ( ^{u 2 +} v ²) ⁺ f² .

Если же коэффициенты различны, то точного решения не существует. Действительно, подставляя (1) в (2), и проводя несложные преобразования, получим, что * и_v * *™ • Это условие показывает невозможность точного восстановления функции * ( и , v ) из уравнений (2) при условии (1). Таким образом, задача расчета функции эйконала может быть решена только численно, из условия выполнения масштабирования (1) с наименьшей погрешностью.

сплайн	сплайн
сплайн 0	сплайн

Рис. 1. Пример представления функции эйконала в первой четверти в виде системы из четырех бикубических сплайнов

Табл. 1. Зависимость СКО освещенности на выходной плоскости от коэффициента масштабирования k ₂

и углового размера а при k 1 = 10 , a = 20 мм

Угловой размер по оси Ох в градусах СКО освещенности на выходной плоскости k2 = 3 k2 = 5 k 2 = 7 k 2 = 10 30 0.0272 0.0356 0.0297 0 20 0.0112 0.0146 0.0130 0 15 0.0089 0.0097 0.0084 0 10 0.0071 0.0075 0.0068 0 шанной производной в углах сплайнов. Будем считать их параметрами оптимизации. Введем функционал невязки, определяющий ошибку выполнения заданного преобразования (1):

F (c ) = Z( x (u, v)-ku )2 +(У (u, v) — k2 v )2, u,v где c – вектор, содержащий значения функции и смешанной производной в узлах системы сплайнов. Вектор параметров c предлагается определять из условия минимума функционала (5). Расчет функции эйконала был реализован в программной среде Matlab 6.5. Для минимизации функционала (5) использовалась встроенная функция fminsearch, использующий симплексный метод Недлера-Мида.

Функция эйконала была рассчитана для случая преобразования равномерного распределения освещенности из квадратной области размером a x a в прямоугольную область размером k1 a x k2a в плоскости z = f . Расчет проводился для различных соотношений коэффициентов масштабирования k1 , k2 и угловых размеров области по оси Ox при a = 20 мм. Угловой размер а = arctg(k1 a/ f) определялся относительно начала координат в плоскости z = 0. Аппроксимация эйконала в первой четверти производилась четырьмя сплайнами (рис. 1). Этого оказалось достаточно для снижения среднеквадратичной ошибки (СКО) формирования постоянной освещенности в выходной плоскости до нескольких процентов. Расчетные значения СКО при различных значениях k1 , k2 , α приведены в табл. 1 и не превышают 3.5%. При этом энергетическая эф- фективность, определяемая как доля энергии, переносимая из области определения эйконала в заданный прямоугольник k1 a x k2 a, для всех указанных в таблице случаев фактически равна 100%. Вид функции эйконала для случая k1 = 10, k2 = 7, а = 20° показан на рис. 2. Результаты расчета распределения освещенности приведены на рис. 3 и показывают формирование прямоугольника с фактически постоянной освещенности. Расчет освещенности в плоскости z = f проводился численно на основе формулы

E ( x, У ) = Eо ( u, v ) / J ( u, v )|,

/ х дx ду ду дx где J (u, v) = — -— ~~ - якобиан лучево-ди д v ди д v го преобразования координат.

Приведенная на рис.2 функция эйконала осуществляет операцию масштабирования для любого распределения освещенности в плоскости z = 0. В качестве примера на рис. 4. приведен результат расчета освещенности в выходной плоскости при функции эйконала, показанной на рис.2 и при равномерном распределении освещенности в круге с радиусом 10 мм. В этом случае формируется эллиптическая область с фактически постоянной освещенностью.

Заключение

Разработан численный метод расчета функции эйконала для выполнения операции масштабирования в непараксиальном приближении. Проведен расчет функций эйконала для различных коэффициентов масштабирования по осям координат. Рассмотрены

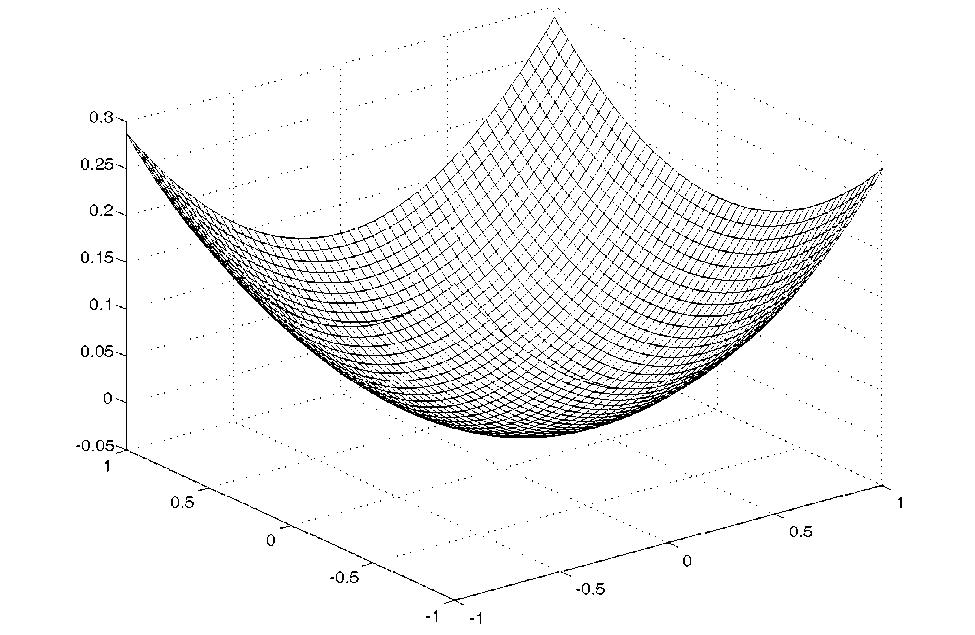
Рис. 2. Функция эйконала, производящего масштабирование с коэффициентами к 1 = 10, к 2 = 7 при угловом размере по оси x а = 20 ° , a = 20 мм

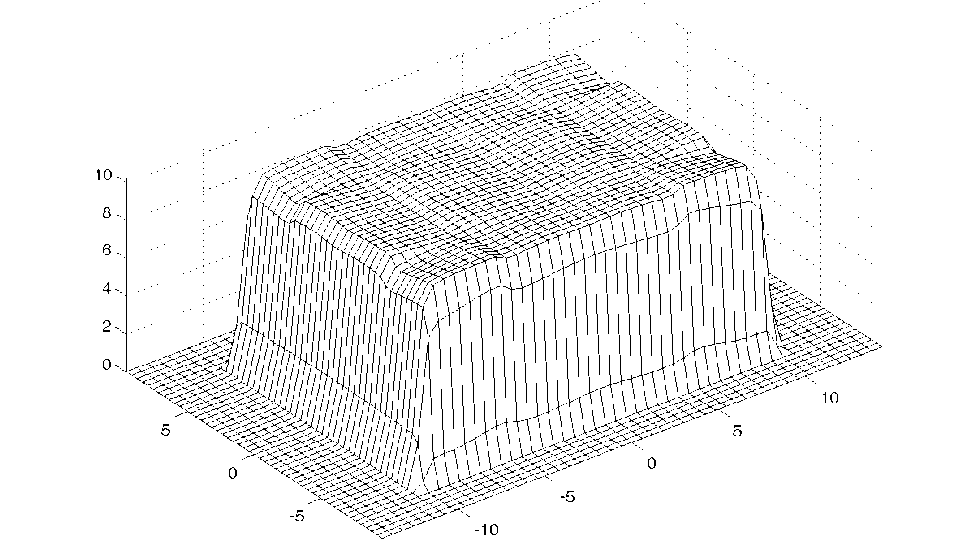
Рис. 3. Расчетное распределение освещенности на выходной плоскости при функции эйконала, показанной на рис. 2

Рис. 4. Расчетное распределение освещенности на выходной плоскости при функции эйконала на рис.2 и равномерной освещенности в круге радиуса 10 мм

примеры преобразования квадратной и круглой областей с постоянной освещенностью в прямоугольную и эллиптическую области, соответственно. Среднеквадратичное отклонение освещенности в выходной плоскости от постоянного значения не превышает 3,5% при угловых размерах масштабированной области до 30є и существенно различных коэффициентах масштаба. Метод допускает обобщение на случай выполнения разделимого преобразования координат общего вида.