Расчет электромагнитного поля в продольно-регулярных структурах

Работы, посвященные определению электродинамических характеристик регулярных линий передачи (в том числе и распределение электромагнитного поля), можно условно разделить на несколько групп.

К первой группе следует отнести работы, в которых электродинамические параметры определяются на основе замены анализируемой структуры приближенной расчетной моделью. В большинстве работ используется либо квазистатическое или коротковолновое приближение, либо модель Олинера [1]. Эти приближенные методы анализа основаны на априорном эвристическом предположении о характере поля в модели. На основе такого подхода рассчитаны характеристики большого числа регулярных линий передачи и различных функциональных элементов [2]. Характеристики линий передач и функциональных элементов описываются достаточно простыми аналитическими выражениями в замкнутой форме, однако главный недостаток такого подхода заключается в том, что установить адекватность реальной анализируемой структуры и ее эвристической модели не представляется возможным. Оценить степень точности модели и сделанных допущений оказывается задачей более сложной и трудоемкой, чем решение самой задачи.

Ко второй группе следует отнести работы, в которых электродинамические характеристики анализируются численными методами с минимальной аналитической обработкой анализируемой структуры. К таким методам относятся метод минимальных автономных блоков [3] и метод сингулярных интегральных уравнений, основанный на интегральных представлениях электромагнитного поля для каждой кусочно-однородной области структуры [4]. Эти методы являются наиболее универсальными и позволяют анализировать наиболее сложные структуры (структуры с некоординатными границами, продольно-нерегулярные линии передачи, нелинейные структуры). Однако они не являются оптимальными для расчета характеристик продольно-регулярных линий передач, ибо получаемые численные результаты не позволяют выявить существенные особенности анализируемой структуры.

К третьей группе следует отнести работы по определению электродинамических характеристик регулярных линий передачи методом частичных областей [5] и методом сингулярных интегральных уравнений [6]. Эти методы являются предпочтительными для расчета характеристик продольнорегулярных линий передачи и позволяют рассчитать их электродинамические характеристики с достаточной точностью. Целью работы является разработка методики расчета составляющих электромагнитного поля в продольно-регулярной линии передачи.

• 1 . Выражения для составляющих полей в продольно-регулярной линии передачи

Поперечное сечение продольно-регулярной линии передачи (рис.1) представим в виде первой (1) и второй (2) областей, в общем случае имеющих разные абсолютные диэлектрические s a 1 , s a 2 и маг-

Рис.1.Поперечное сечение анализируемой структуры

Известно, что для регулярных линий передач продольная зависимость электромагнитного поля описывается множителем e ^{i Y} z . Тогда электрическое и магнитное поля в E -ой ( E =1,2) области можно записать в виде

Е ^ ( x , У , z ) = E ^ ( x , y ) ■ e - ^{i Y} z ,

H l e ( x , У , z ) = H E ( x , У ) ■ e - i ^Y , где у -продольное волновое число.

В этом случае уравнения Максвелла, описывающие электромагнитное поле внутри анализируемой структуры, сводятся к однородным уравнениям Гельмгольца, решение которых известно. Из них нужно выбрать такие, которые удовлетворяют граничным условиям для касательных составляющих электрического ЕТ и нормальных составляющих магнитного H n полей на идеально проводящей внешней поверхности S анализируемой структуры

E T s = 0, ^H - I s * 0.

С учетом этих граничных условий при симметричном распределении поля относительно плоскости x = 0 продольные составляющие электрического и магнитного полей определяются соотношениями to

E1 z (x, У)=   Z A1 m ■ cos(Y xm m =1,3,5,...

■ x ) ■ ^{sin (} Y y 1 ■ У ) ,

to                                              ,            .

^H 1 z ^{( x}, У ) =    Z B 1 m ■ ^{sin (} Y xm ■ ^x У co^{s (} Y y 1 ■ У ) , ⁽²⁾

m = 1,3,5,...

^E 2 z ^{( x} , У ) =

= Z A2m ■ cos(Yxm ■ x) ■ sin(Yy2 ■ (У2 - У J’ m =1,3,5,...

^H 2 z ^{( x} , У ) =

=    Z B 2 m ■ ^sin ( / xm ■ ^x У co ^{s (} Y у 1 • ( У ^{2 -} У Л’     ⁽⁴⁾

m = 1,3,5,...

где

• 2           „,2   „,2                m m

Y yc   k^  У   У xm , У xm   2 x 2 , k^ = ^jea^Ma5 ■

Зная выражения для продольных составляющих электрического и магнитного полей, с помощью известных соотношений можно определить и остальные составляющие в анализируемой структуре i-to

Ex1(x, y) = 2   Z (A1 m " Y ■ Y xm + k 1 m =1,3,5,..

+ B1 m ■ ®- Ma 1 ■ Yу 1 У sin(Yxm ■ x)x x sin(YУ1 ■ У),

Ey 1(x, У) = “if   Z(- A1 m ■ Y ■ Yу 1 + k 1 m=1,3,5,..

+ B1 m ■ to ■ Ma1 ■ Yxm У cos(Yxm ■ x) x x cos(Y у 1 ■ У),

i

H x 1(x, y ) =   2   Z (B1 m " Y ■ Y xm - k 1 m =1,3,5,..

• ^-    A 1 m ■ ®' Y a 1 ■ Y y 1 У ^{cos (} Y xm ■ ^{x ) x (7)}

x cos ⁽ Y y 1 ■ У ) ,

i

Hy1 (x,y ) = 2   Z (B1 m ' Y ■ Y y 1 + k 1 m=1,3,5,^

+ A1 m ■ to- £a 1 ■ Yxm )■ sin(Yxm ■ x)x x sin(Yy 1 ■ У), i^x/

Ex 2 (x, y) = 2"   Z (A 2 m ' Y ■ Y xm + k2 m=1,3,5,^

+ B 2 m ■ to- Ma 2 ■ Yy 2 )■ sin(Yxm ■ x)x x cos(Yy2 •(У2 - У)), i ro

Ey2(x,y) = -2   Z(- A2m ■ Y ■ Yy2 + k2 m=1,3,5,^

⁺ B 2 m ■ ^to' M a 2 ■ ^Y xm ) ■ ^cos ( ^Y xm ■ ^{x ) x        (10)}

x cos(Yy2 •(У2 - У)), i to

Hx 2 (x,y ) =    2"   Z (B 2 m ' Y ■ Y xm - k2 m=1,3,5,^

• ^-    A 2 m ■ ^to ^ a 2 ■ Y y 2 ) ■ ^{cos (} Y xm ■ ^{x ) x        (11)}

2. Расчет амплитудных коэффициентов

^{x cos (} Y y 2 ■ ( У ^{2 -} У ) ) , i ^to

Hy2(x,У) = — Z(B2m ■ Y ■ Yy2 + k2 m=1,3,5,^

⁺ A 2 m ■ ^to ■ ^ a 2 ■ ^Y xm ) ■ ^{sin ( Y} xm ■ ^{x ) x         (12)}

^{x sin (} Y y 2 ■⁽ У ^{2 -} У ) ) ■

В этих соотношениях для составляющих полей неизвестные коэффициенты A1m , B1m , A2m , B2m и величины y , Yy 1, Yy2 подлежат определению из граничных условий в плоскости расположения центрального проводника.

Для определения неизвестных коэффициентов

A^m , B^m и величин Y, Yy 1, Yy2 необходимо вос- пользоваться граничными условиями для касательных составляющих электрического и магнитного полей в плоскости расположения центрального проводника, которые сводятся к уравнениям

A 1 m ■ ^{sin (} Y y 1 ■ У 1 ^{) =} A 2 m ■ ^sin (y y 2 ■ ⁽ У ^{2 -} У^     ⁽¹³⁾

2 (A1 m ' Y ■ Y xm + B1 m ' to ■ Ma 1 ■ Y y 1 )x k1

x sin ⁽ Y y 1 ■ y l ) =    ⁽ A 2 m ■ Y ■ Y xm +              ⁽¹⁴⁾

k 2

⁺ B 2 m ■ ^to ■ M a 2 ■ Y y 2 ) ■ ^{sin (} Y y 2 ■ ⁽ У ^{2 -} У ¹ ) ) ■

Из этих соотношений можно выразить коэффи- циенты A2m, B2m, через A1m, B1m:

л                  s^{in (} Y У 1 ■ У 1 )

A 2 m = A 1 m ■ —t --, ^sin ( y y 2 ■ ( У ^{2 -} У ¹ ) )

^B 2 m

A          ^{sin (} Y y 1 ■ У ¹ )

¹ m ^{sin (} Y y 2 ■⁽ У ² - У ¹ ) )

( , 2     ^

k ² - 1 ■   ^YY xm

[ k 1²     ) ^to' M _o 2 V y 2

B         ^{sin (} Y У Г У ¹ )      M a 1 -У У 1 ■ k 2

^{+ 1 m sin (} Y y 2 ■ ( У ^{2 -} У ¹ ) ) M a 2 V y 2 ■ k 1² ■

Определим неизвестные постоянные коэффициенты A ^ _m , B ^ _m , ( ^ = 1, 2) входящие в соотношения

(1) - (12), через касательные составляющие электрического поля в первой области E 1 _z ( x , y ) , E 1 _x ( x , y ) в плоскости центрального проводника при y = у 1 ■ Для этого левую и правую части соотношения (1)

умножим на cos ( g _xm ■ x ) и, используя условие орто-

гональности, получим
A           2
1 m x 2 ■ sin ( g y 1 ■ y 1 )
x 2                                       . x J E 1 z ( x , У ) ■ cos ( Y xm ■ x ) dx 0 Аналогично из соотношения (5): B _________________ 2 ■ k 12      , B 1 m = i ■ to ■ M a 1 ■ Y y 1 ■ x 2 ■ sin ( Y y 1 •		(17)
	x ' У 1 )
x 2
x J E x1 ( x , У ) ■ sin ( Y xm ■ x ) dx -
0		(18)
___________ 2 ■ Y ■ Y xm ________
to' M a1 ■ Y y 1 ■ x 2 ■ sin ( Y y 1 ■ У 1 )
x 2
x J E 1 z ( x , У ) ■ cos ( g xm ■ x ) dlx .
0
С учетом обозначений
2 x 2 e zm =—;■ J E 1 z ( x , У 1 ) ^ cos ( Y xm ■ x ) x 2 0	dx ,	(19)
2 x 2 e xm = — ■ [ E 1 x ( x , У 1 ) ^ sin ( Y xm ■ x ) x 2 0	dx ,	(20)
соотношения (17), (18) запишутся в виде:
1 A 1 m      . (         .1 e zm , sin ( Y y 1 ■ У 1 ) k 12 B 1 m = ■ ,               ■ /        Л i ■ to- M a1 ■ Y y 1 ■ sin ( Y y 1 ■ y 1 )		(21)
	e xm .	(22)
Y ■ Y xm
й e zm to' M a1 ■ Y y 1 ■ sin ( Y y 1 ■ У 1 )

Тогда касательные составляющие магнитного поля в первой области в плоскости расположения центрального проводника при y = у1 можно запи- сать в виде

Hx 1(x, У1) =   Е^П m^ ezm + m =1,3,5,™           ,

+ Yn ■ e xm ) • ^{cos (} Y xm ■ ^x )

Hz 11x, У1) =   Z(Y21m ■ ezm + m =1,3,5,™           ,

+ Y 22 ) ■ e xm ) ■ ^{sin (} Y xm • ^x ) где

Y ( 1 )      i ^Y ■ ^Y xm + k 1 ■ ^Y y 1

11 m   k 2 to- Ца1 ■ Y y1     X, x ctg (Y y 1 ■ У1)

m=-to Y       ■ ctgY 1 ■ y1),(26)

^to' M a 1 ' Y y 1

Y21m = — «, Y■ Yxm-  ■ ctgYУ y1),(27)

^{to Ц} а1 Y y 1

Y2Hm = "----~ctg (Yy1 ■ y1).

I ■ to - Ц а 1 ■ ^Y y 1

Для второй области при y = y1 получим выра- жения для Hx2 , Hz2 , аналогичные соотношениям (23), (24)

Hx 2 (x, У 1)=  Ш ezm + m=1,3,5,™           ,

⁺ YlS ■ exm У co^{s (} Y xm ■ ^x )

Hz2 (x, У1) =   E(YПт ■ ezm + m=1,3,5,™            ,

• ^{+ Y} 22 m ■ e xm ) ■ ^{cos (} Y xm ■ ^x )

где

• Y ( 2 ) = i ^{Y 2} ■ ^Y xm ^{+ k} 2 ■ ^Y 22 _x

• 11 m   k2      to- Ца2 ■ Yy2    X,

^x ctg ⁽Y y 2 ⁽ У ^{2 -} У ¹ ) )

YSm =- „ Y,■ Yxmm   ■ ctg(Yy2 (У2 - У1)),(32)

^to' M a 2 ■ Y y 2

YSm =Y        ■ ctg (yy 2 (y 2 - y1)),(33)

^to' M a 2 ■ Y y 2

• Y) "-----ctg Yy 2 (У 2 - У1)).(34)

i ■ ^to M a 2 ■ Y y 2

Ток проводимости на поверхности центрального проводника определяется касательной составляющей магнитного поля. Представим составляющие тока проводимости в виде ряда Фурье:

^

J zэ J xэ	Е j zm ■ cos t		.Y xm ■ x ) ,		(35) (36)
	m = 1,3,5, ™ ^ = Е j zx m = 1,3,5, ™	■ sin ( ;
			xm ■	x ) ,
где
jzm	x 2 = — J э z ' ■ x 2 J z	cos ( g	7 xm ■	x ) d^x ,	(37)
	0
j xm	x 2 = - [4 x x 2 0	■ sin ( g	' xm ■	x ) dx .	(38)

С учетом граничных условий на поверхности центрального проводника и соотношений (23), (24), (29), (30) получим:

jzm jxm

^Y 11 m ■ e zm ⁺ Y 12 m ■ e xm ,

= ^Y 21 m ■ e zm ^{+ Y} 22 m ■ e xm ,

где

Y pqm

= Y ^{( 1 )}

r pqm

-

у ^{( 2 )}

pqm ^,

p , q = 1,2.

Систему уравнений (39) можно преобразовать к виду e zm exm

^z 11 m ■ ^j zm ^{+ z} 12 m ■ j xm ^,

= ^z 21 m ■ j zm ^{+ z} 22 m ■ j xm ,

где

• ^Y 22 m              ^Y 12 m              ^Y 21 m

• 3. Результаты расчета электромагнитного поля в анализируемой структуре

z 11 m = ” , ^z 12 m = у— , z 21 m = ~— , Y_m             Y_m             Y_m

Y11m z22m =      , Ym = Y11 m ' Y22m — Y12m ' Y21 m ■

Ym

Зная распределения тока, можно по приведенным выше соотношениям рассчитать электромагнитное поле в регулярной линии передачи.

Распределение тока может быть определено после решения дисперсионного уравнения, которое может быть сведено к сингулярному интегральному уравнению [6].

Рассмотренная выше методика была применена к расчету составляющих электромагнитного поля в экранированной Т-камере. В ее регулярной части отсутствует диэлектрическое заполнение, а внутреннюю поверхность и центральный проводник можно считать идеально проводящими. При этих условиях параметры первой и второй сред одинаковы S a 1 = S a 2 = e о , M a1 = M a 2 = M 0 ■ Так как центральный проводник расположен симметрично, то поперечная составляющая тока проводимости J_x обращается в ноль, а продольная составляющая тока в первом приближении распределена по центральному проводнику равномерно [6]. Эти особенности распределения тока проводимости позволяют по изложенной выше методике рассчитать структуру электрического и магнитного полей без решения дисперсионного уравнения.

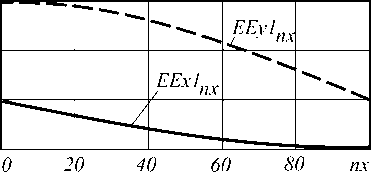
На рис.2-3 в качестве иллюстрации приведены зависимости нормированных составляющих электрического и магнитного полей от нормированной поперечной координаты в заданном сечении анализируемой структуры y = y 0. На этих рисунках со-

1,0

0,5

-0,5

в)

Рис. 2. Распределение составляющих электрического поля в анализируемой структуре при y 0 /y 1 =0.025 (а), y 0 /y 1 =0.5 (б), y 0 /y 1 =0.75 (в)

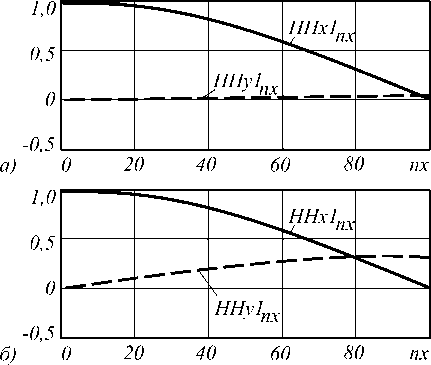
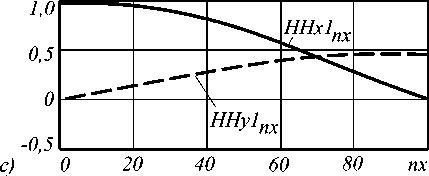
Рис.3.Распределение составляющих магнитного поля в анализируемой структуре при y₀/y₁=0.025 (а), y 0 /y 1 =0.5 (б), y 0 /y 1 =0.75 (в)

Составляющие магнитного поля нормировались ставляющие электрического поля нормировались относительно максимального значения горизон-

относительно максимального значения вертикальной составляющей

тальной составляющей

EEx1 =

E x 1 ⁽ x , У ^{0 )}    , _{EEy 1} = E y 1 ^{( x} , ^{у 0 )}

max { E y 1 ( x , у 0 ) } ’         max { E y 1 ( x , у 0 ) }

HHx1 = —Hx1 (x,y 0)   , max{Hx 1(x, y 0)}

HHy l = H y 1 ^{( x} , ^{y 0 ) max {} H x1 ( x , y ^{0 )}} ,

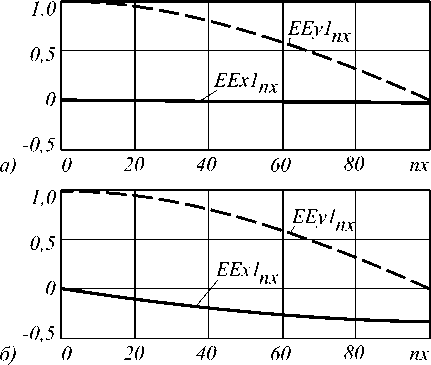
а координата x по оси абсцисс отложена в процен-

тах nx = — - 100 ⁰ x 2

Полученные результаты позволяют определить неравномерность поля в анализируемой структуре.

Заключение

Получены аналитические выражения для составляющих электрического и магнитного полей в регулярной линии передачи, выраженные через распределение тока проводимости на центральном проводнике. В приближении равномерного распределения продольной составляющей тока проводимости на центральном проводнике рассчитано распределение электрического и магнитного полей в анализируемой структуре.