Расчет энергетических коэффициентов отражения и пропускания для слоистых периодических сред

DOI:

В настоящее время большое внимание уделяется изучению фотонных кристаллов – материалов с упорядоченной структурой, характеризующейся строго периодическим изменением коэффициента преломления в масштабах, сопоставимых с длинами волн излучений в видимом и ближнем инфракрасном диапазонах [1; 2; 4–12; 14–21]. Это динамично развивающееся направление современного материаловедения. Оно связано с возможностью создания светодиодов с высоким КПД, новых типов лазеров с низким порогом генерации, световых волноводов, оптических переключателей, фильтров, а также устройств цифровой вычислительной техники на основе фотоники.

Отличительной особенностью таких материалов является структура, которая характеризуется периодическим изменением показателя преломления. Данные кристаллы всех типов могут рассеивать некоторое излучение при условии, что параметры решетки кристалла имеют тот же порядок, что и длина волны излучения. Подобным образом, будучи прозрачными для широкого диапазона электрического излучения, фотонные кристаллы не пропускают свет с длиной волны, сопоставимой с временем структуры фотонного кристалла.

Расчеты

В данной работе рассмотрена плоская волна, которая падает на слоистую периодическую среду (рис. 1).

Рис. 1. Падение плоской волны на слоистую периодическую среду (угол падения 9 = 45°; толщина слоев: 1 = 100 нм; 2 = 160 нм; 3 = 80 нм; 4 = 120 нм)

Она занимает область от z = 0 до z = z ₁ и с обеих сторон граничит с однородными по-лубесконечными средами. Получено выражение для амплитуд и интенсивности отраженной и прошедшей волн.

Обозначим A , R и T амплитуды электрических векторов падающей, отраженной и преломленной волн. Пусть е 1 , ц 1 и е ₂, ц ₂ - диэлектрические и магнитные проницаемости граничных сред, а 9 1 и 9 2 - углы между нормалями к падающей и прошедшей волнами и направлениями оси z .

Слоистая периодическая среда с периодом h характеризуется диэлектрической проницаемостью е и магнитной проницаемостью ц , зависящими только от z; они имеют вид

е(z + jh) = е(z) ц(z + jh) = ц(z), где j – любое целое число из некоторого фиксированного интервала I < j < N.

Пусть M ( h ) – характеристическая матрица, соответствующая одному периоду.

Запишем

M ( h )=

m ₁₁

m ₂₁

m ₁₂

m ₂₂

В этом случае, в соответствии с

I              Q 0 = M ( z n ) Q ( z n )

t M ( ^zN ) = M 1 ( z_x ) M 2 ( z 2 ^- z 1 ) *...* M N ( ^zN ^{- z}N -1 )    ⁽ )

и с учетом периодичности среды, получим

M [ Nh ] = M ( h "M ( h ) _ M ( h ) = [ M ( h )] ^N .    (3)

Многослойная система состоит из чередующихся однородных слоев с показателями преломления n ₂, n ₃, ... n_{k -1} и толщинами h ₂, h ₃, ... h_{k +1,} расположенных между двумя однородными средами с показателями преломления n ₁ и n_l (рис. 2).

Мы снова считаем среду немагнитной (ц = 1) и полагаем в , = — nh, cos6,

TE ^X ₀ j j j p j = n j cos 6 j

Характеристическая матрица М_k ( h ) одного периода имеет вид

M k ( h ) =

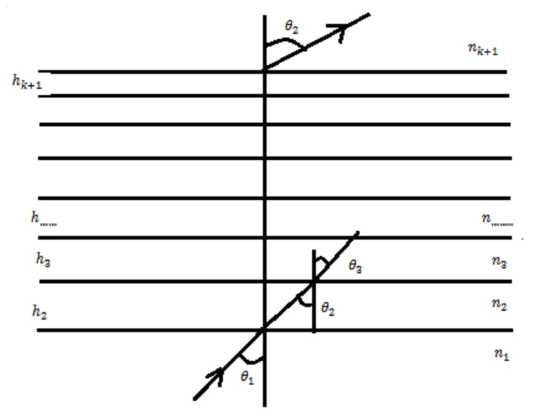
Рис. 2. Периодическая многослойная система

cosβ2

- ip 2 sin в 2

i

--sine 2

p ₂

cosβ2

i cose3

.    . „       p 3 „*

• -    ip3Sine3

^cos^e k + 1       ^- — ^sin^e k + 1

Pk + 1

.^- p + 1 ^sin^e k + 1       ^cos^e k + 1

Характеристическая матрица Мk(h) одного периода имеет вид h = h 2 + h 3 + ^ + hk+1

M k ( h ) =

cosβ2

- iq ₂ sine₂

i

--sine2

q ₂

cosβ2

Следовательно, в соответствии с выражением (3) характеристическая матрица М_kN ( Nh ) многослойной системы (с полным числом пленок N ) будет считаться как произведение:

i cose3--sine3 q 3         *

• -    iq ₃sine 3     cose₃

cos^e k + 1      -- — ^sin^e k + 1

q k + 1

.^{- i} q_k + 1 ^sin^e k + 1        ^cos^e k + 1

M kN ( Nh )=

M 11

M 21

M 12

M 22

Коэффициенты отражения и пропускания многослойной системы:

Следовательно, в соответствии с выражением (3) характеристическая матрица М_kN ( Nh ) многослойной системы (с полным числом пленок kN ) определяется следующими формулами, полученными Абеле:

r = ^R = ^{( M} 11 ^{+ M} 12 p 3 ) p 2   ^{( M} 21 ^{+ M} 22 p 3 )    (7)

A (M11 + M12 p 3 )p 2 +(M 21 + M 22 p 3 ) , t _ T_  ______________2 p 2_______________

A  ^{( M} 11 ^{+ M} 12 P 3 ) P 2 ^{+ ( M} 21 ^{+ M} 22 p 3 )   ^ ^

M kN ( Nh )=

^M 11

^M 21

^M 12

M 22

Коэффициенты отражения и пропускания многослойной системы:

Аналогичным образом получаем такую же характеристическую матрицу для волны ТМ-типа:

^R = ^{( M} 11 ^{+ M} 12 q 3 ) q 2 ^{-( M} 21 ^{+ M} 22 q 3 ) A ⁽ M 11 ⁺ M 12 ^q 3 ) ^q 2 ^{+( M} 21 ^{+ M} 22 ^q 3 )

в, = “ ⁿ,h, cos6,

TM ^ j ¹ X₀ ^{11    1}

q j = n j cos 6 j

>

t = T =2 q 2 .

A  ^{( M} 11 ^{+ M} 12 q 3 ) p 2 ^{+( M} 21 ^{+ M} 22 q 3 )

Также для реализации расчета периодической слоистой среды вместо прямого произведения характеристических матриц можно воспользоваться расчетом результирующей матрицы с помощью полиномов Чебышева [3]:

[M (h)] N = m11UN-1(a )  UN-2 (a)

m 21^U N - 1 ⁽ a )

m12 UN-1 (a )       , m 22UN-1 (a ) — UN-2 (a 1

где a = 2 (m11

+ m 22 X

а U_N – полиномы Чебышева второго рода:

^UN ⁽ x ) =

sin [( N + 1 ) arccos x ]

V I - x²

Эти полиномы удовлетворяют следующим условиям ортогональности и нормировки:

+1              ______ 0; n * m

[ U, ( x ) U ( x )V 1 - x ² dx\ n ^m n                 ; n * m

- 1                                 12

Существует возможность подсчетов полиномов Чебышева по реккурентной формуле:

U о ( x ) = 1

U , ( x ) = 2 x

U n + , ( x ) = 2 xU n ( x ) - U n - , ( x )

В частности, получим:

U 2 ( x ) = 4 x ² -1

U 3 ( x ) = 8 x ³ - 4 x

U ₄ ( x ) = 16 x ⁴-12 x ²+1

U 5 ( x ) = 32 x ⁵ - 32 x ³ + 6 x

Реализация расчетов на языке С++

Для реализации расчетов было создано консольное приложение на языке С++. В начале опишем вспомогательные компоненты программы. В подключаемом файле Complex.cpp описан класс Complex, реализующий создание и арифметические операции с комплексными числами. В структуре реализованы такие операции, как сложение, умно- жение комплексных чисел, умножение комплексного числа на рациональное, нахождение сопряженного и модуля. Построение графических объектов осуществляется с помощью программы TXLib.h. Далее мы не будем акцентировать внимание на типе данных конкретной переменной. Основное тело программы состоит из единой функции main. Тело функции можно условно разделить на основные части:

• 1.    Создание первичных данных.

• 2.    Расчет необходимых параметров и построение характеристической матрицы для определенного угла падения.

• 3.    Сохранения коэффициентов отражения и пропускания в выходной файл.

• 4.    Построение графического изображения поведения коэффициентов отражения и пропускания для первичной оценки построенной модели.

• 5.    Входными данными программы является: количество слоев N ; толщины слоев h [ N- 1]; показатель преломления n [ N ], длина волны падающего света l 0.

Результаты расчетов

1-й результат сравнения.

На рисунке 3 представлен угловой спектр коэффициентов отражения и пропускания ( a - угол падения) при прохождении через слоистую периодическую структуру (MgO/C/AsBr₃/Si). Толщины слоев: 100 нм, 160 нм, 80 нм, 120 нм. Длина падающей волны: 640 нм. Количество повторений структуры: 5. Входные данные программы: n [ N ] = {1,3.09,2.38,1.87,3.42,1}, l 0 = 640, h [ N -1] = {0,100,160,80,120}, С = 5.

На рисунке 4 представлен угловой спектр коэффициентов отражения и пропускания при прохождении через слоистую периодическую структуру (MgO/C/AsBr₃/Si) при использовании полиномов Чебышева. Толщины слоев: 100 нм, 160 нм, 80 нм, 120 нм. Длина падающей волны: 640 нм. Количество повторений структуры: 5. Входные данные программы: n [ N ] = {1,3.09,2.38,1.87,3.42,1}, l 0=640, h [ N -1] = {0,100,160,80,120}, С=5.

2-й результат сравнения.

На рисунке 5 представлен угловой спектр коэффициентов отражения и пропуска- ния при прохождении через слоистую периодическую структуру (MgO/C/AsBr3/Si). Толщины слоев: 100 нм, 160 нм, 80 нм, 120 нм. Длина падающей волны: 640 нм. Количество повторений структуры: 15. Входные данные программы: n[N] = {1,3.09,2.38,1.87,3.42,1}, l0=640, h[N-1] = {0,100,160,80,120}, С = 15.

На рисунке 6 представлен угловой спектр коэффициентов отражения и пропускания при прохождении через слоистую периодическую структуру (MgO/C/AsBr3/Si) при использовании полиномов Чебышева. Толщины слоев: 100 нм, 160 нм, 80 нм, 120 нм. Длина падающей волны: 640 нм. Количество повторений структуры: 15. Входные данные программы: n[N] ={1,3.09,2.38,1 .87,3.42, 1}, l0=640, h[N-1] = {0,100,160,80,120}, С = 15.

Выводы

В результате выполнения данной работы был описан алгоритм созданного пакета прикладных программ, который получил официальную регистрацию в реестре программ

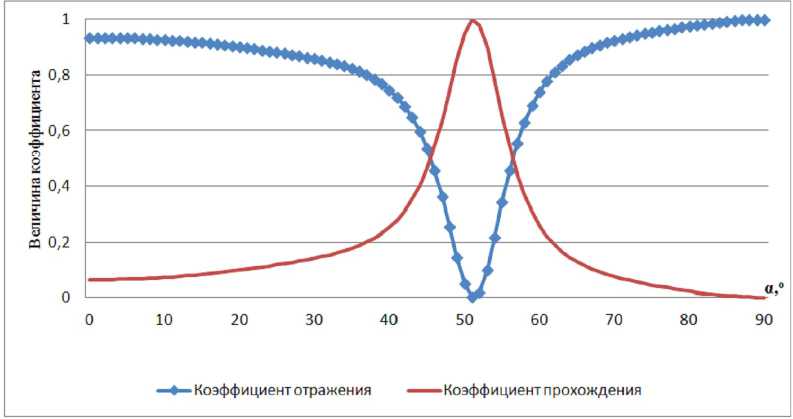
Рис. 3. Угловой спектр коэффициентов отражения и пропускания ( α – угол падения) при прохождении через слоистую периодическую структуру (MgO/C/AsBr₃/Si)

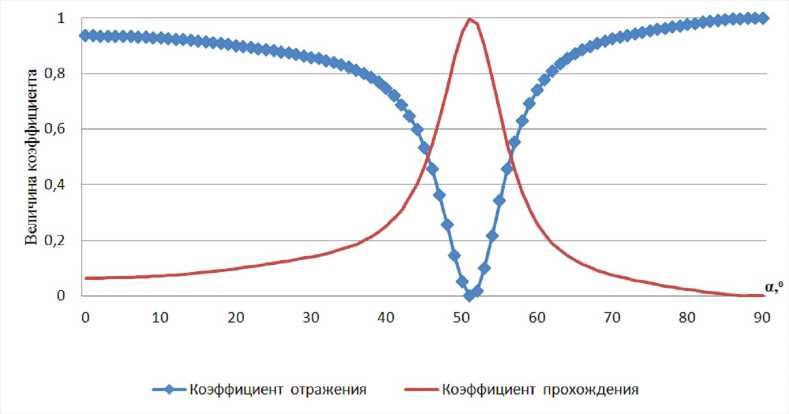
Рис. 4. Угловой спектр коэффициентов отражения и пропускания при прохождении через слоистую периодическую структуру (MgO/C/AsBr3/Si) при использовании полиномов Чебышева

для ЭВМ [13]. Проведены расчеты энергетических коэффициентов отражения и пропускания для слоистой периодической среды из следующих компонентов: слой оксида магния MgO толщиной 100 нм, слой алмаза толщиной 160 нм, слой мышьяка трибромид AsBr3 толщиной 80 нм, слой кремния Si толщиной 120 нм. Показано, что спектральная зависимость этих коэффициентов представляет собой ярко выраженную интерференционную картину. Из этой картины можно извлекать информацию о структуре слоистой периодической среды. Полученные результаты могут быть положены в основу решения спектральных задач для слоистых периодических сред и фотонных кристаллов. Важным результатом работы является проведение сравнения метода характеристических матриц и метода на основе полиномов Чебышева: при большем количестве периодов отклонение либо равно 0, либо меньше ограничений языка программирования. Показано, что в целом они дают одинаковые результаты для периодических структур.