Расчет энергии делокализации атома в бескислородных стеклах

В рамках модели делокализованных атомов Сандитова [1; 2] для свободной энергии активации вязкого течения выведено уравнение, учитывающее две со- ставляющие, вторая из которых зависит от температуры и энергии делокализа- ции атома:

ЛГ ^ -AF + RT

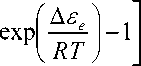
здесь Δε e — энергия делокализации атома, R — универсальная газовая постоянная, ΔF_∞ — потенциал перескока кинетической единицы в структуре вещества. Вторая часть уравнения, зависящая от температуры, есть не что иное, как потенциал местной трансформации структуры ΔF s (T). Данное уравнение соотносится с представлениями теории Немилова [3; 4] о том, что свободная энергия активации вязкого течения складывается из двух потенциалов: переключения мостиковой связи (к примеру переключение атома кислорода в системе Si–O–Si) и трансформации структуры вещества в области переключения мостика. В валентноконфигурационной теории Немилова формула для данной энергии записывается так:

ЛГ , -AF + лг _t ( T ) , (2)

где Δ F η⁰ — потенциал переключения мостиковой связи, Δ F η k — потенциал конфигурационного изменения структуры.

Важным обстоятельством является то, что обе формулы в явном виде указывают на температурную зависимость свободной энергии активации вязкого течения. При помощи подбора параметров Δ F _∞ и Δε _e такая зависимость может достаточно хорошо показана в большом диапазоне температур (до 200 градусов) [7; 8].

Представленный в формуле (2) вариант описания свободной энергии, характеризующей активацию вязкого течения, который учитывает два слагаемых, имеет свое отражения в различных теориях. При этом одно из слагаемых практически не зависит от температуры, а вторая в том или ином виде имеет температурную зависимость. Впервые такое видение энергии активации было отражено в работах Филипповича [5; 6].

Зависимое от температуры слагаемое Δ F _{η k} ( T ) в формуле Немилова (2) уменьшается, если температура растет, при этом явный вид такой зависимости не приводится [3; 4]. Численные значения этой части энергии активации могут быть определены из данных о конфигурационной части молярной теплоемкости при постоянном давлении C p конф ( T ).

В настоящей работе будет показано, что формула (1) удовлетворительно показывает справедливость предположения о том, что свободная энергия активации вязкого течения зависит от температуры и от одной из двух составных частей потенциала переключения мостиковой связи. Представляется вариант расчета не зависящего от температуры слагаемого Δ F ∞ и расчет энергии делокализации атома Δε e , являющегося параметром развиваемой модели делокализованных атомов [8; 9]. Заявленные составы стекол будут исследованы в значительном диапазоне изменения температуры.

Расчет

С вероятностной точки зрения процесс перескока кинетической единицы (атома) в новое равновесное положение зависит от двух условий, которые учитываются одновременно. К таким условиям, несомненно, относится возможность изменения локальной структуры для изменения положения атома, а также нали- чие у этого атома достаточной энергии для перехода в новое положение. Поэтому можно считать, что вероятность данного события, являющегося в некотором роде элементарным актом вязкого течения, есть произведения вероятностей этих двух составных условий: W = W1W2, где W1 и W2 — вероятности локального изменения структуры и накопления энергии для перескока соответственно. При этом в развиваемой модели первый множитель связан с вероятностью так называемой делокализации атома [1; 2].

Термин «делокализация атома» в одноименной модели для рассматриваемых, в том числе неорганических стеклообразных, материалов подразумевает смещение мостикового атома вследствие деформации структуры с валентными связями. Делокализация атома связана в целом с локальным изменением структуры, потому что она имеет место быть только в том случае, если вблизи мостикового атома появляется элементарный флуктуационный объем Δv e [10; 11].

Форма уравнения (1) подразумевает относительное постоянство энергии делокализации атома Δεe в рамках того температурного диапазона, в котором в явном виде имеется зависимость ΔFη(T) [2; 7]. Далее приводится расчет энергии делокализации, который показывает относительное его постоянство, однако имеются и некоторые отклонения.

Таким образом, из уравнения (1) с учетом предположения о том, что Δεe прак- тически не зависит от температуры, можно записать выражение:

ASe = RT In к

AFn

AT co

RT

+1

J

по которому и будет произведен расчет числовых значений данного параметра модели делокализованных атомов в температурном интервале в 100–200 граду- сов.

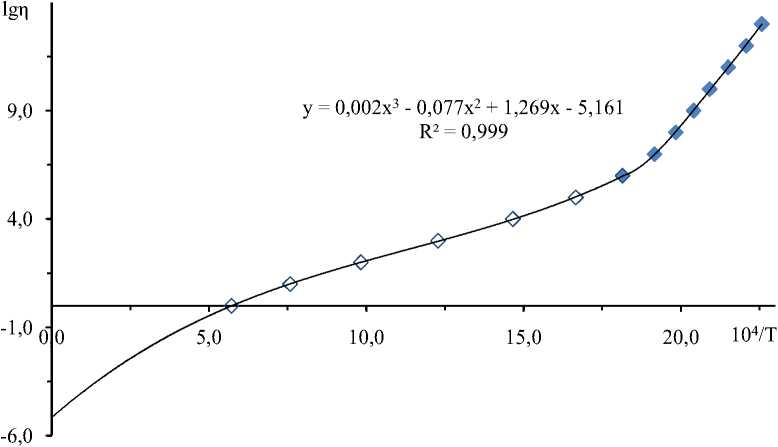
Рис. 1. Значения логарифма вязкости стекла системы As — Se в зависимости

от величины, обратной температуре. Закрашенные ромбы — экспериментальные данные [12], пустые ромбы найдены по полиному Лагранжа

Первое зависимое от температуры слагаемое уравнения (1) ΔFη(T) можно определить из известного уравнения Эйринга [11]. Для этого необходимо знать экспериментально определенные значения вязкости составов в разрезе температур. Значение энергии изменения локальной структуры вблизи мостикового атома выражается в виде:

^AF n = RT [ ln П ^{( т} ) - ln П 0 ] •                            (4)

Данные о значениях логарифма вязкости при достаточно большом наборе значений температуры взяли из справочных данных [12; 13]. Здесь ln η 0 — высокотемпературный предел вязкости, который можно найти путем экстраполяции графика зависимости ln η от обратной величины температуры в виде значения логарифма вязкости при бесконечной температуре (рис. 1). Полученная кривая в координатах lg η — 10 ⁴ /T для стекла типа As — Se, как показывает графический метод, соответствует уравнению полинома 3-й степени:

y = 0,0046x ³ - 0,1516x ² + 1,9594x - 6,9481.

Величина достоверности аппроксимации: K2 = 0.999. Перевод десятичных логарифмов в натуральные осуществлен перемножением на 2,3.

Свободная энергия перехода атома в следующее устойчивое положение ΔF∞ в научной литературе имеет физический смысл значения потенциала активации текучести при бесконечной температуре ΔF∞ = ΔFη (T→∞) и, соответственно, остается неизменным при различных конечных температурах. В удовлетворительной мере согласованное значение постоянной для данного состава слагаемой энергии активации вязкого течения можно получить исходя из данных об эмпирических параметрах C1 и C2 уравнения Вильямса — Ландела — Ферри (ФЛФ) [14]:

afm= RQC2.

Уравнение ВЛФ является одним из наиболее удачных для демонстрации температурной зависимости вязкости η (T) в области стеклования [11, с. 31]:

t - T lg a_T =-C -----^,

• ⁶ T ¹ T - T + C₂

где a_T = η( T )/η( T_g ) — относительная вязкость.

Если учитывать, что в данном уравнении C 1 и C 2 — постоянны, то переписанное уравнение ВЛФ должно иметь график линейной зависимости в координатах: –( T – T g ) / lg a T — ( T – T g ):

• - ^{( t - T g} ) = — (t - T ) +C ².

lga _T      C ₁      ^g    C ₁

Для расчета относительной вязкости можно определить примерное значение логарифма вязкости при температуре стеклования графическим методом. Его значение, если не прибегать к дополнительным расчетам, можно взять за 13. Для системы As — Se (Tg = 443 K) значение составило lg ηg = 13,54.

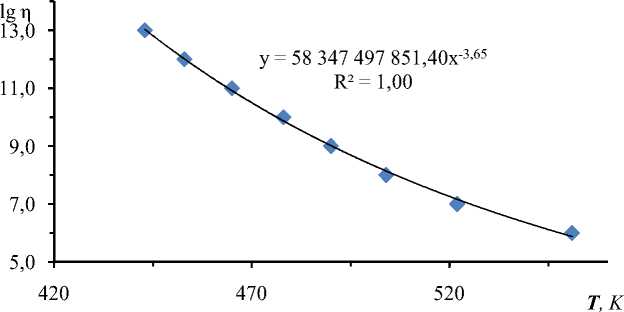
Рис. 2. График зависимости логарифма вязкости от температуры по экспериментальным данным [12] для стекла системы As — Se

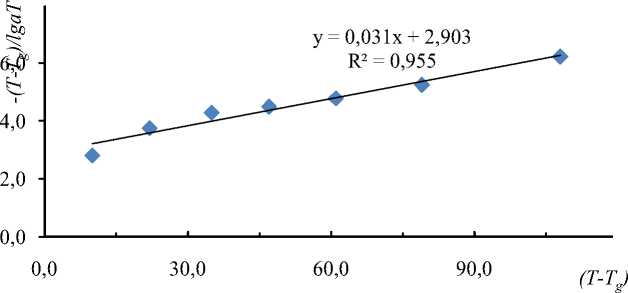
Рис. 3. График зависимости вязкости стекла типа As — Se от температуры в координатах: – (T–T g )/lg a T — (T–T g ).

График в координатах – (T–T_g)/lga_T — (T–T_g), как и следовало ожидать, имеет форму линейной зависимости. Данный факт оправдывает применимость уравнения ВЛФ для бескислородных неорганических стекол в заданном интервале значений температуры. По данным полученного графика, а именно по уравнению линии тренда, приняв уравнение прямой достаточно точным для описания зависимости, можно записать значения эмпирических параметров уравнения ВЛФ. Для стекла системы As — Se значение C 1 = 32,1, а значение C 2 = 93,1 K. В соответствии с этим энергия перехода атома в новое положение (5) равно

kF^= 24803,03 Дж / моль.

В итоге полученные значения зависящей от температуры Δ F _η( T ) и одно значение Δ F ∞ , которое не зависит от температуры, можно подставить в формулу (3) и получить значения энергии делокализации атома для рассматриваемых стекол. В таблице 1 показаны полученные данные для стекла 40As–60Se.

Таблица 1

Данные для расчета свободной энергии активации вязкого течения ΔF_η (T) и энергии делокализации атома Δε e для стекла 40As–60Se

T, K	lg (η, П)	ΔF η (T)	ΔF ∞	Δε e
		кДж/моль
443	13	153,85		13,20
453	12	148,66		13,27
465	11	143,71		13,37
478	10	138,59	24,803	13,47
490	9	132,69		13,50
504	8	126,85		13,55
522	7	121,39		13,66
551	6	117,60		14,00

Примечание: использованы данные [12].

Для состава 40As–60Se, по которому показаны промежуточные расчеты, значение энергии делокализации составляют 13,2 — 14,00 кДж/моль. Для 40As– 40Se–20Ge Δε e = 15,69 — 16,48 кДж/моль, а для составов 35BeF 2 — 20AlF 3 — 45RF 2 Δε e = 9,43 — 14,73 кДж/моль. Значения энергии делокализации атома, как показывают расчеты, практически не меняются и имеют относительно постоянную величину около температуры стеклования (рис. 4). Величина данной энергии чуть меньше, чем у силикатных стекол, у которых она на уровне 21 кДж/моль. Данная разница, по-видимому, возникает из-за сильного различия в типах стекол: исследуемые стекла — бескислородные халькогенидные и алюмосодержащие, а силикатное стекло — кислородсодержащие, в которых мостиковым атомом является атом кислорода. В трехкомпонетном алюмосодержащем стекле вследствие отличительных свойств алюминия более выраженная зависимость энергии делокализации атома от температуры в пределах 5 кДж/моль.

20,00

1 10,00

< 5,00

0,00 "I---------------1---------------1---------------1---------------1---------------1---------------1

425           475           525           575

T, K

Рис. 4. Значения Δε _e , рассчитанные по формуле (3), для стекла системы As — Se

С другой стороны, в модели делокализованных атомов Сандитова [9; 10] численные значения энергии делокализации атома можно рассчитать по данным о доле флуктуационного объема f g , замороженного при температуре стеклования:

^A ^ e = ^RTg ln ⁽ 1 f g ) . (8) где f_g = ( A V_e/V ) T = T . Как говорилось выше, энергия перестройки локальной структуры вблизи мостикового атома связана с энергией делокализации атома, которая, в свою очередь, есть функция доли флуктуационного объема ΔV e , возникающей в результате выхода колеблющегося атома из равновесного положения. Этот объем собирается из N_e делокализованных атомов, каждый из которых занимает элементарный флукутационный объем Δv e ,:

A V = N_e A v _е.

Значение доли флуктуационного объема для стеклообразных веществ колеблется в небольшом диапазоне около 2–3%. В модели делокализованных атомов f g равняется обратной величине параметра уравнения ВЛФ C 1 [9]

f = X - co^t - 0.020 — 0.030 . ^g

C ₁

Для рассматриваемых составов стекол по данным о величине f g получены величины энергии делокализации атома. Для 40As–60Se значение Δε _e = 12,76 кДж/моль. Для 40As–40Se–20Ge Δε _e = 17,40 кДж/моль, а для составов 35BeF₂ — 20AlF 3 — 45RF 2 Δε e = 19,38 кДж/моль. Эти данные удовлетворительно соотносятся с данными расчетов по температурной зависимости вязкости исследуемых стекол.

Заключение

Энергия делокализации атома Δε _e в исследованных составах мало изменяется в зависимости от температуры в области T_g . Хотя для бескислородных составов такая закономерность прослеживается хуже, чем у кислородсодержащих силикатных стекол. Для алюмосодержащих составов зависимость уже становится более заметной. Данные также были рассчитаны по параметрам модели делокализованных атомов, полученные значения Δε _e также приблизительно совпадают со значениями по разобранному в работе методу.