Расчет кавитационного обтекания рабочего колеса радиально-осевой гидротурбины

При замыкании кавитационных пузырьков происходит также значительное местное повышение температуры жидкости, что приводит к её свечению и к активации химических, в частности, коррозионных процессов. Эксперименты показали, что реальные жидкости практически не выдерживают растягивающих напряжений. Это объясняется наличием в любой реальной жидкости включений газовых пузырьков или частиц твёрдых тел. Эти включения называют зародышами (ядрами) кавитации, именно они делают столь низкой объёмную прочность воды, поэтому в реальных условиях работы гидротурбины при наличии турбулентных пульсаций, вихрей в пограничном слое, местных неровностей на обтекаемых поверхностях, неизбежных твёрдых и органических включений кавитация возникает при осреднённых давлениях, близких к давлению парообразования жидкости

В гидротурбинах, в основном, возникает профильная кавитация на лопастях рабочих колёс, которая имеет различные формы и стадии в зависимости от геометрии лопасти и режима работы гидротурбины [2, 3]. На начальной стадии возникает пузырьковая кавитация, которая проявляется в виде отдельных пузырьков, образующих в области минимума давления и сносимых по потоку. По мере развития кавитации она принимает форму пленочной, при которой происходит образование заполненных паром кавитационных каверн, состоящих из стационарной головной части и пульсирующей хвостовой части каверны. Для пленочной кавитации характерно усиление шума и вибрации гидротурбины, разрушение материала лопастей рабочего колеса. При развитой пленочной кавитации шум и вибрация становятся недопустимыми для эксплуатации, происходит резкое снижение (срыв) внешних параметров гидротурбины: напора, расхода, мощности и КПД. Изложенное показывает, что совершенствование расчетных методов кавитационного обтекания рабочих колес гидротурбин, позволяющих исследовать отрицательные последствия кавитации на работу гидротурбины, является в настоящее время весьма актуальной задачей, имеющей большое практическое значение.

Численное моделирование кавитационных течений. Как уже отмечалось, необходимым условием возникновения кавитации в какой-либо точке на лопасти рабочего колеса является уменьшение давления в этой точке до давления насыщенных водяных паров . Разность между давлением в любой точке лопасти и давлением парообразования р_в.п определяется по формуле [2]:

( P - P в.п ) ₌ p gH    ° уст

CT тур

где σ уст – кавитационный коэффициент установки, равный

° уст

' ^p б ^р в.п J _ H s ₌ p уст р в.п ) I p gH J H    p gH

р_б – барометрическое давление на нижнем бьефе, Н S – высота отсасывания (условная величина, характеризующая высоту расположения рабочего колеса гидротурбины над уровнем нижнего бьефа), ρ – плотность жидкости, H – напор, p_уст = р_б – ρgH_S – давление установки (условная величина давления, позволяющая при расчете моделировать различные стадии кавитации в гидротурбине).

Значения кавитационного коэффициента турбины σ _тур в рассматриваемой точке лопасти определяются в результате расчета распределения давлений р по поверхности лопасти рабочего колеса по формуле:

_ ( p уст ^р ) _

° тУР    pgH     cP где ср – коэффициент давления.

При бескавитационном обтекании значения σ тур во всех точках лопасти меньше заданной величины σ уст . Заметим, что величина σ уст меняется при изменении значения р _уст (см. формулу (2)), а величина σ тур при бескавитационном обтекании лопасти не зависят от значения р уст , поскольку при изменении р уст на какую либо величину на такую же величину меняются во всех точках лопасти значения давлений. При уменьшении σ _уст (например, за счёт изменения р уст ) до значения σ тур давление становится равным давлению водяных паров, что является условием возникновения кавитации.

В настоящее время разработаны программы расчета трехмерного турбулентного течения вязкой жидкости, которые позволяют определить на заданном режиме распределение коэффициентов давления (или кавитационных коэффициентов турбины) по лопасти рабочего колеса. В частности, в данной работе расчет трехмерного вязкого турбулентного течения жидкости проводился на основе осредненных по Рейнольдсу уравнений Навье-Стокса c использованием программного комплекса FINE™/Turbo [4]. В расчете принималась стандартная k^ε модель турбулентности. Наиболее распространенным подходом к моделированию кавитационных течений является модель сплошной среды. В данной работе при расчете кавитации рассматривается баротропная модель [5], в которой изменение плотности среды связано с изменением статического давления баротропным законом. В этом случае для моделирования кавитации может быть принята модель однофазной смеси, которая характеризуется переменной плотностью, изменяющейся в пределе расчетной области. Баротропный закон ρ(p) используется для оценки местной плотности в зависимости от местного статического давления (рис.1). Расчетные ячейки в этом случае рассматриваются как полностью заполненные жидкостью (ρ=ρλ), паром (ρ=ρv) или их смесью в зависимости от величины давления в ячейке. Плотность и динамическая вязкость смеси определяются выражениями:

p = aPv + 1- a pv

Ц = a^v + (1- a \ix

Индексы X и v относятся к плотности и динамической вязкости чистой жидкости и пара. Коэффициент a= V'VV_яч характеризует объемную долю пара в расчетной ячейке, где V яч – объем расчетной ячейки, V _V - объем пара в ячейке. Для определения объема пара в ячейке используется уравнение Рэле-я-Плесса [4, 5], описывающее динамику процесса роста и захлопывания пузырьков:

d d ² Л 3 [ dR ? _ P en - р _ю _^л dR_ 2 ° 0

dt 2^ dtJ    px    R dt pr

^Я .       (5)

где R радиус пузырька, σ 0 – коэффициент поверхностного натяжения, p _∞ - давление смеси вне пузырька, p в.п – давление пара в пузырьке.

В рассматриваемой баротропной модели зависимость ρ ( p ) определяется из условия:

с

2 dP m dp

где с m – скорость звука в гомогенной смеси, которая связана со скоростями звука в чистой жидкости с л и в паре c _V следующей зависимостью:

-12- = [«pv +(1 - a ^ipA.-Ол + 1771 ст                  ]_ pvcv plcl

Используя зависимость (7), в результате интегрирования уравнения (6) определяется плотность смеси в зоне изменения статического давления p_v + Δp (рис. 1). В данной работе задавалось значение Δp =1400 Па и принималось условие, что минимальное значение скорости звука в гомогенной смеси, равное c_min =1 м/c, имеет место при величине давления парообразования p v =2350 Па.

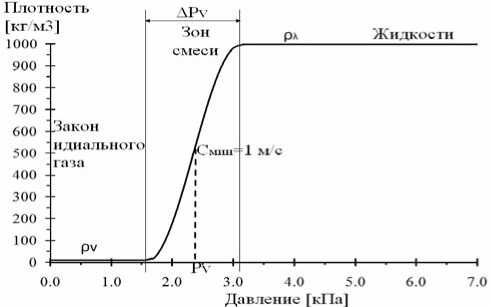
Рис. 1. Баротропный закон состояния воды при температуре 20^oC

Расчет кавитационого обтекания гидротурбины PO 230/833/ В данной работе с помощью прикладной программы FINE/TURBO^TM проведен расчет трехмерного течения вязкой жидкости в проточной части гидротурбины РО230/833.

Геометрическая модель турбины была построена с помощью программного комплекса ГРАНИТ [1]. При расчете использовалась экономичная гексои-дальная расчетная сетка. Расчеты производились на персональном компьютере в циклической постановке, при которой в области рабочего колеса и направляющего аппарата рассматривается один межлопастной канал. Расчет производился для эталонной гидротурбины с диаметром рабочего колеса D 1 =1 м при напоре Н=1 м. На рис. 2 показаны геометрия лопаток направляющего аппарата (при открытии a₀ =65 мм) и лопастей рабочего колеса, а также представлен фрагмент расчетной сетки (задавалось 800000 узлов расчетной сетки в области рабочего колеса и 1200000 узлов в области направляющего аппарата). Для корректного расчета течения в областях с большими градиентами изменения параметров потока (в области пограничного слоя), расчетная сетка имела сгущение.

Рис. 2. Геометрия лопаток направляющего аппарата и лопастей рабочего колеса гидротурбины РО230/833 и фрагмент расчетной сетки

Расчет проводился для режима работы гидротурбины, близкого к оптимальному режиму (приведенные обороты n 1 =70 об/мин, приведенный расход Q 1 =0,5204 м³/с). На входе в расчетную область задавались параметры потока: радиальная скорость V_r =0,563 м/с, окружная проекция скорости V u =0,67м/с и осевая скорость V z =0,0 м/c. Необходимо также задать значение давления установки р уст , от которого существенно зависит режим кавитационного обтекания. Значения статических давлений во входном и выходном сечениях определяются в зависимости от величины р уст по формулам:

V2

Р вх = Р уст - Р"^ + P gH

2

вых p вых  p уст г ~

2                (8)

На рис. 3 показано распределение значений кавитационного коэффициента турбины с турб = с р ( 5 ) по периферийному сечению лопасти рабочего колеса при задании различных значений кавитационного коэффициента установки (или давления установки р у _ст ). При величине о_уст =0,5 имеет место режим бескавитационного обтекания данного сечения лопасти. При задании с уст =0,10 на тыльной стороне сечения лопасти в районе выходной кромки возникает кавитационная каверна, в которой давление практически постоянно и близко к давлению парообразования. При дальнейшем уменьшении величины с_уст =0,05 область кавитационной каверны становится более развитой. При этом увеличивается отличие распределения давления по лопасти от эпюры распределения давления для случая ее бескавитационного обтекания (при ^с уст ^0,5) .

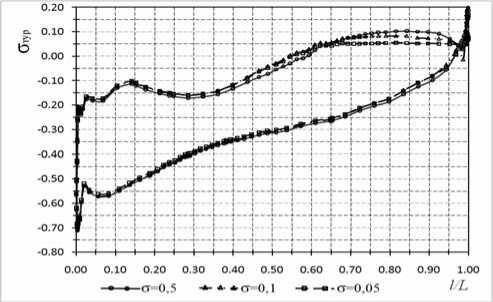
Рис. 3. Распределения σ тур = f ( l ) по периферийному сечению лопасти рабочего колеса РО833 при различных значениях σ уст

На рис. 4 показано распределение плотности смеси по тыльной стороне периферийного сечения лопасти при различных значениях σ уст . Видно, что в зоне кавитации с уменьшением σ уст в соответствии с баротропным законом плотность смеси уменьшается до 700 кг/м³ по сравнению с плотностью жидкости, равной 1000 кг/м³.

Вывод: выполненные расчетные исследования гидротурбины РО230/833 показали, что с помощью программного комлекса FINE/TURBO^TM можно эффективно определить кинематику трехмерного турбулентного потока вязкой жидкости в проточной части гидротурбины и оценить влияние различных стадий кавитации на гидродинамические характеристики гидротурбины.