Расчет коэффициента теплопроводности нанокристаллов
Автор: Северюхин А.В., Северюхина О.Ю., Вахрушев А.В.
Статья в выпуске: 1, 2022 года.
Бесплатный доступ
Методы математического моделирования являются мощными инструментами при проектировании различного типа наносистем и анализа протекающих в них процессов. Отметим, что главными задачами математического моделирования в наномасштабных системах являются: формирование наноэлементов, взаимодействие отдельных элементов наносистемы, определение структуры изолированной наносистемы в динамических состояниях, расчет параметров наносистемы при взаимодействии с окружающей средой, расчет макропараметров наносистемы. Данной работой мы продолжаем последовательное изложение теоретических основ, методов моделирования и результатов расчетов макрохарактеристик наносистем, основанных на работах по моделированию процессов формирования и структуры различных наносистем. В данной работе приводятся физические основы, а также численные методики расчета коэффициента теплопроводности однородных наносистем. Компьютерное моделирование расчета коэффициента теплопроводности нанокристаллов на основе кремния методом молекулярной динамики было проведено в программном комплексе LAMMPS. Рассмотрены уравнения, описывающие многочастичные потенциалы MEAM. Решение задачи определения коэффициента теплопроводности было осуществлено в несколько этапов. В молекулярно-динамических расчетах величину коэффициента теплопроводности можно вычислить различными способами. В данной работе используется формализм Грина - Кубо (Green - Kubo), который связывает автокорреляционную функцию теплового потока с коэффициентом теплопроводности. Определены температурные зависимости коэффициента теплопроводности для материалов на основе кремния. Выполнены расчеты теплофизических характеристик однородных наносистем на основе кремния. Представлены кривые температурной зависимости коэффициента теплопроводности для систем различной размерности. Проведено сравнение данных, полученных с использованием потенциалов MEAM с экспериментальными данными. Выявлено, что характер кривых и значения, полученные при моделировании, хорошо согласуются с экспериментальными данными.
Модифицированный метод погруженного атома, теплопроводность, молекулярная динамика, моделирование, эксперимент, нанокристалл, lammps
Короткий адрес: https://sciup.org/146282431
IDR: 146282431 | УДК: 536.2.02
Текст научной статьи Расчет коэффициента теплопроводности нанокристаллов
ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2022PNRPU MECHANICS BULLETIN
Теплопроводность можно определить как количество тепла, передаваемого через единицу толщины материала – в направлении, нормальном к поверхности единицы площади, – из-за единичного температурного градиента в условиях устойчивого состояния. Теплопроводность – необходимая характеристика для рассеивания образовавшейся тепловой энергии в системе. Прогресс нанотехнологий за последние два десятилетия предоставил разнообразные системы с высокой теплопроводностью из различных типов материалов и топологических форм.
Определение такой характеристики, как теплопроводность материала, является задачей, которой посвящено множество теоретических и экспериментальных исследований. Ввиду этого использование методов математического и компьютерного моделирования является перспективным для описания моделей процессов теплообмена.
В данной работе приведены результаты расчетов теплофизических характеристик наносистем. В представленной статье в продолжение предыдущих исследований авторов [1; 2] рассмотрена задача расчета коэффициента теплопроводности однородных наносистем.
Отметим, что решению задачи определения коэффициента теплопроводности кремния на наноуровне посвящен обширный ряд работ. В исследовании [3] коэффициент теплопроводности равен 20 Вт/(м·К), а в работе
-
[4] – 235 Вт/(м·К). В статье [5] при моделировании использовался потенциал Стиллингера – Вебера, коэффициент теплопроводности равен 20 Вт/(м·К). В исследовании [6] коэффициент теплопроводности получился 37–43 Вт/(м·К). Отметим, что в источнике [7] получена диаграмма значений коэффициента теплопроводности для систем различной размерности.
1. Постановка задачи
Моделирование системы проводилось с помощью программного пакета LAMMPS [8] методом молекулярной динамики [9]. Выбор потенциала взаимодействия играет важную роль при моделировании. В настоящее время для кремния доступно огромное количество многочастичных потенциалов. Наибольшее распространения при моделировании металлических и полупроводниковых систем применяют EAM (метод погруженного атома) потенциалы [10; 11] и MEAM (модифицированный метод погруженного атома) потенциалы [12–15]. В данной работе использовался потенциал взаимодействия MEAM.
Задача расчета коэффициента теплопроводности может быть решена несколькими способами. Их описание можно найти в работах [16; 17]. В данной работе для определения теплофизических свойств наносистем использован метод Грина – Кубо.
Решение задачи определения коэффициента теплопроводности осуществляется в несколько этапов.
На первом этапе происходит формирование необходимой наноструктуры, которая помещается в расчетную ячейку с периодическими граничными условиями по осям x , y , z.
Второй этап предполагает достижение равновесного состояния моделируемой системы посредством применения NPT ансамбля. Графики температуры и давления на протяжении данного этапа представлены на рис. 1, 2. Целью данного этапа является релаксация системы, при которой расчетная ячейка моделирования доводится до равновесного объема при заданных температуре, давлении и числе атомов. Скорости атомов масштабируются таким образом, чтобы при моделировании температура держалась на заданном уровне. Данный этап должен быть достаточно продолжительным, чтобы система уравновесилась. После достижения равновесия, постоянная решетки не будет существенно изменяться и колебаться. В молекулярной динамике важную роль играет выбор временного шага интегрирования, так как он определяет точность и эффективность расчета. Если временной шаг мал, то требуется больше времени вы- числений для достижения желаемого времени моделирования. Если шаг велик, то большие силы могут развиваться на более легких атомах, что приведет к искусственно быстрым атомам. В работе используется шаг по времени 0,2 фс. Тестовые расчеты показали, что такая величина шага является подходящей для решения данного класса задач.
Третий этап предполагает достижение равновесного состояния моделируемой системы посредством применения NVE ансамбля. На этом этапе моделирования объем ( V ) и полная энергия ( E ) системы «заморожены» из-за применения ансамбля NVE. «Удаление» термостатирования ( T ) и баростатирования ( P ) освобождает атомные движения из-за искусственного изменения масштаба.
На рис. 3 представлен график температуры на протяжении всего третьего этапа моделирования. Видно, что система держит температуру в районе 300 К без применения термостатов.
На рис. 4, 5 представлены графики общей энергии и объема расчетной ячейки на протяжении всего третьего этапа моделирование NVE.
Рис. 1. График температуры системы 4 x 4 x 4 на втором этапе моделирования при температуре 300 К
Рис. 2. График давления системы 4 x 4 x 4 на втором этапе моделирования при температуре 300 К
Fig. 1. Temperature graph of a 4 x 4 x 4 system at the second stage of modeling at a temperature of 300 K
Fig. 2. Pressure graph of a 4 x 4 x 4 system at the second stage of modeling at a temperature of 300 K
Шаг по времени, ед.
Рис. 3. График температуры системы 4 x 4 x 4 на третьем этапе моделирования при температуре 300 К
Рис. 4. График энергии системы 4 x 4 x 4 на третьем этапе моделирования при температуре 300 К
Fig. 3. Temperature graph of a 4 x 4 x 4 system at the third stage of modeling at a temperature of 300 K
Fig. 4. Energy diagram of a 4 x 4 x 4 system at the third stage of modeling at a temperature of 300 K
Шаг по времени, ед.
а
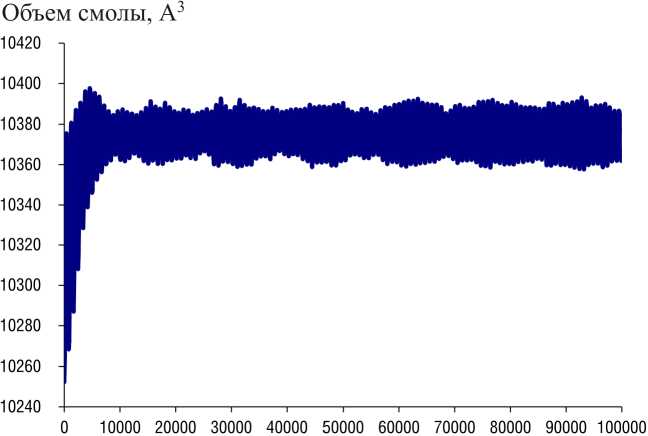
Объем смолы, А3
б
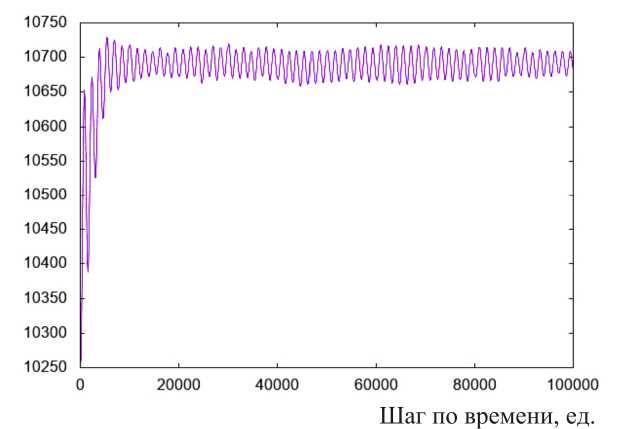
Рис. 5. График изменения объема расчетной ячейки системы 4 x 4 x 4 на третьем этапе моделирования при температуре: а – 300 К; б – 1000 К
Fig. 5. The graph of the change in the volume of the computational cell of the 4 x 4 x 4 system at the third stage of modeling at a temperature of: а – 300 K; б – 1000 K
2. Расчет коэффициента теплопроводности
В молекулярно-динамических расчетах величину коэффициента теплопроводности можно вычислить различными способами [8].
В данной работе используется формализм Грина – Кубо (Green – Kubo), который связывает автокорреляционную функцию теплового потока с коэффициентом теплопроводности. Тепловой поток может быть рассчитан из колебаний потенциальной и кинетической энергии атома и тензора напряжения атома в стационарном уравновешенном моделировании. Это отличие от двух предыдущих неравновесных методов молекулярной динамики (NEMD), где энергия течет непрерывно между горячими и холодными областями в моделируемом образце.
Коэффициент теплопроводности в модели Грина – Кубо рассчитывается по следующей формуле [18; 19]:
1τ
-
k = liimlim ^ T2 dd L JJ ( t ) J ( 0 )) dt , (1) t ^^ L ^^ KI *0
B где k – коэффициент теплопроводности d – мерной системы с линейным размером, T – температура, kB – постоянная Больцмана, J – компонента потока тепла.
Постоянная времени τ – это минимальное время, необходимое для того, чтобы автокорреляционная функция теплового потока затухала до нуля. Этот метод более подходит для анизотропных систем. Основным недостатком этого метода является то, что для затухания до нуля автокорреляционной функции теплового потока требуется много времени, а получаемые значения теплопроводности зависят от размера системы.
Автокорреляционные функции справа в формуле (1) оцениваются в равновесии, без градиента температуры. Автокорреляция – статистическая взаимосвязь между случайными величинами из одного ряда, но взятыми со сдвигом, например, для случайного процесса – со сдви- гом по времени. Автокорреляционная функция может быть определена как:
Ψ(τ)= ∫ f ( t ) f ( t –τ) dt .
Общий тепловой поток в системе вычисляется как J(t)=∫ j(x, t)dx, где j(x,t) – плотность теплового потока.
Порядок пределов в формуле (1) имеет большое значение. При правильных порядках пределов можно вычислить корреляционные функции с произвольными граничными условиями и применять формулу (1). Существуют различные формы записи уравнения (1) [20–25].
Существуют ситуации, когда формула (1) неприменима. Во-первых, для маленьких систем, которые изучаются в мезоскопической физике, термодинамический предел не имеет смысла. Во-вторых, во многих низкоразмерных системах перенос тепла аномальный и теплопроводность существенно отклоняется от экспериментальных значений [26; 27]. В таких случаях невозможно взять пределы в формуле (3). Поэтому тепловую проводимость рассматривают как функцию от длины L . В литературе, посвященной этой тематике [26; 27], обычно в формуле (1) меняют верхний предел интегрирования tc на L . Другой способ использования формулы Green – Kubo для конечных систем заключается в том, чтобы внедрять бесконечные резервуары, как это сделано в работах [28; 29].
В данной работе для расчета теплопроводности кремниевых наноструктур был выбран метод Green – Kubo. Для вычисления коэффициента теплопроводности использовалась следующая запись формулы (1) [8; 30]:
k = f U ( 0 ) J. ( t )) dt =---1—r [( J ( 0 ) x J ( t )) dt ,
-
Vk B T 2 0 xx 3 Vk B T 2 0
где V – объем системы.
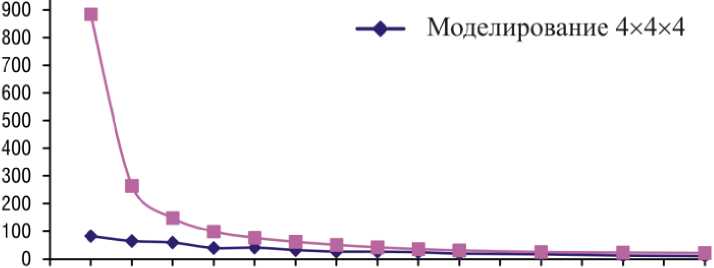
На рис. 6 и 7 приведены значения коэффициента теплопроводности чистого кремния при различной температуре в сравнение с экспериментальными данными. Полученные в нашей работе значения хорошо согласуются с таковыми, представленными в работе для масштабных образцов [32].
Известно, что в металлах и полупроводниках работают два механизма переноса тепла: за счёт электронов и посредством фононов. В чистых металлах процесс переноса тепла осуществляется в основном посредством свободных электронов, концентрация которых на единицу объема в металлах весьма велика. При температурах, близких к абсолютному нулю (T ^ 0 ), концентрация фононов будет мала. Большую роль будет играть электронная теплопроводность. Следует отметить, что в чистых металлах при нормальных условиях теплопро- водность электронного газа много больше решеточной теплопроводности.
На рис. 6, 7 видно, что при повышении температуры, когда фононная проводимость будет играть большую роль, чем электронная, результаты моделирования и экспериментальные данные хорошо согласуются.
Графики, показанные на рис. 8, 9, представляют собой усредненные корреляционные кривые тепловых потоков. Время сбора автокорреляционных данных должно быть достаточно большим, чтобы автокорреляция затухала до нуля.
Были построены графики теплопроводности в различные моменты времени при температуре 300 К (рис. 9) и 1000 К (рис. 10).
Как видно из рис. 10–11, после 20 пс система стабилизируется, и коэффициент теплопроводности выходит на стационарное значение.
Карра, Вт/(м К) 1000 и
0 100 200 300 400 500 600 700 800 900 1000110012001300140015001600
Температура, К
Рис. 6. График теплопроводности, полученный при моделировании системы 4 x 4 x 4, в сравнение с экспериментальными данными
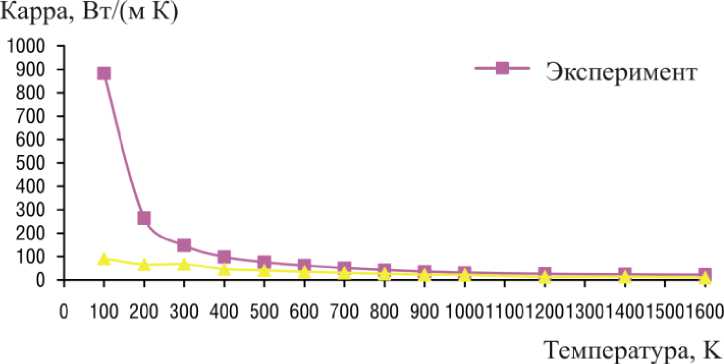
Рис. 7. График теплопроводности, полученный при моделировании системы 10 x 10 x 10, в сравнении с экспериментальными данными
-
Fig. 6. Thermal conductivity graph obtained when simulating a 4 x 4 x 4 system in comparison with experimental data
-
Fig. 7. Thermal conductivity graph obtained when simulating a 10 x 10 x 10 system in comparison with experimental data
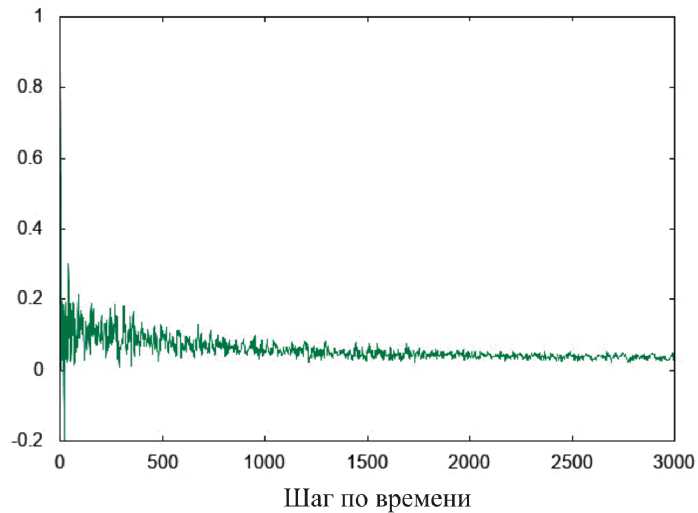
Рис. 8. График автокорреляционной функции теплового потока температуре 300 К
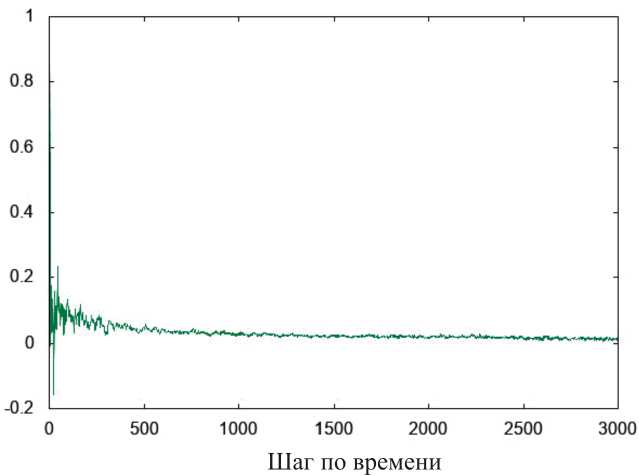
Рис. 9. График автокорреляционной функции теплового потока температуре 1000 К
-
Fig. 8. Graph of the autocorrelation function of the heat flux at a temperature of 300 K
-
Fig. 9. Graph of the autocorrelation function of the heat flux at a temperature of 1000 K
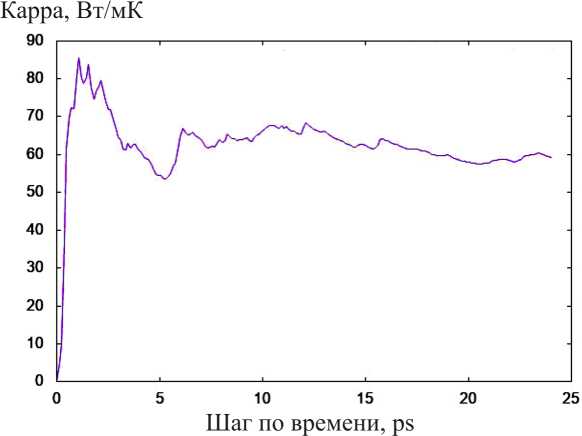
Рис. 10. График теплопроводности при температуре 300 К для системы 4 x 4 x 4
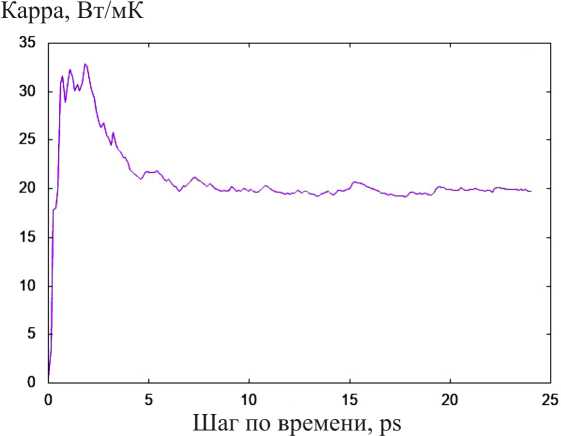
Рис. 11. График теплопроводности при температуре 1000 К для системы 4 x 4 x 4
Fig. 10. Thermal conductivity graph at a temperature of 300 K for a 4 x 4 x 4 system
Fig. 11. Thermal conductivity graph at a temperature of 1000 K for a 4 x 4 x 4 system
Заключение
Построены физическая и математическая модели процессов теплопроводности в наноматериалах на основе кремния высокой плотности с использованием потенциала взаимодействия MEAM. Изложена методика расчета характеристик данного процесса. Также в работе показаны особенности и различия потенциа- лов взаимодействия, используемых в молекулярнодинамических расчетах.
Список литературы Расчет коэффициента теплопроводности нанокристаллов
- Исследование теплофизических свойств наноматериалов на основе кремния методом Green – Kubo с использованием потенциала EDIP / А.В. Вахрушев, А.В. Северюхин, О.Ю. Северюхина, А.Ю. Федотов // Химическая физика и мезоскопия. – 2016. – Т. 18, № 2. – С. 187–198.
- Исследование теплофизических свойств кремниевых наноматериалов методом Green – Kubo / А.В. Северюхин, О.Ю. Северюхина, А.В. Вахрушев, А.Ю. Федотов // Проблемы механики и материаловедения труды Института механики УрО РАН. – Ижевск. – 2016. – С. 210–223.
- Schelling P.K., Phillpot S.R. and Keblinski P. Comparison of atomic-level simulation methods for computing thermal conductivity // Phys. Rev. B. – 2002. – Vol. 65. – P. 144306 (12). DOI: 10.1103/PHYSREVB.65.144306
- Lee Y., Lee S., and Hwang G.S. Effects of vacancy defects on thermal conductivity in crystalline silicon: A nonequilibrium molecular dynamics study // Phys. Rev. B. – 2011. – Vol. 83. – P. 125202 (7). DOI: 10.1103/PHYSREVB.83.125202
- Thermal conductivity reduction in core-shell nanowires / M. Hu, X. Zhang, K.P. Giapis and D. Poulikakos // Phys. Rev. B. – 2011. – Vol. 84. – P. 085442 (9).
- Esfarjani K. and Chen G. Heat transport in silicon from first-principles calculations // Phys. Rev. B. – 2011. – Vol. 84. – P. 085204 (11). DOI: 10.1103/PhysRevB.84.085204
- Slideserve [Электронный ресурс]. – URL: http://www.slideserve.com/guang/modeling-thermal-transport-at-singleinterfaces- and-in-nanostructured-materials-using-non-equilibriummolecular-dynamics (дата обращения: 07.09.2020).
- Lammps [Электронный ресурс]. – URL: https://lammps.sandia.gov (дата обращения 07.10.2020).
- Simulation of the processes of formation of quantum dots on the basis of the transition metals / A.V. Vakhrushev, O.Yu. Severyukhina, A.V. Severyukhin [et al.] // Nanomechanics Sci. Tech. Int. J. – 2012. – Vol. 3. – P. 51–75. DOI: 10.1615/NanomechanicsSciTechnolIntJ.v3.i1.30
- Daw M.S., Baskes M.I. Embedded-atom method: derivation and application to impurities, surfaces, and other defects in metals // Phys. Rev. B. – 1984. – Vol. 29, № 12. – P. 6443–6453. DOI: 10.1103/PHYSREVB.29.6443
- Daw M.S., Baskes M.I. Semiempirical, Quantum Mechanical Calculations of Hydrogen Embrittlement in Metals // Phys. Rev. Letters. – 1983. – Vol. 50, № 17. – P. 1285–1288.
- Daw M.S. Model of metallic cohesion: The embedded-atom method // Phys. Rev. B. – 1989. – Vol. 39, № 11. – P. 7441–7452. DOI: 10.1103/PHYSREVB.39.7441
- Ruda M., Farkas D., Abriata J. Interatomic potentials for carbon interstitials in metals and intermetallics. Scripta Mater. – 2002. – Vol. 46, № 5. – P. 349–355.
- Tomar V., Zhou M. Classical molecular-dynamics potential for the mechanical strength of nanocrystalline composite fcc Al+α-Fe2O3 // Phys. Rev. B. – 2006. – Vol. 73, № 17. – P. 174116.
- Hohenberg P., Kohn W. Inhomogeneous electron gas. // Phys. Rev. B. – 1964. – Vol. 136, № 3. – P. 864–871. DOI: https://doi.org/10.1103/PhysRev.136.B864
- Вахрушев А.В., Северюхин А.В., Северюхина О.Ю. Расчет макрохарактеристик наносистем. Часть 1. Коэффициент теплопроводности однородных наносистем // Химическая физика и мезоскопия. – 2017. – Т. 19, № 2. – С. 167–181.
- Вахрушев А.В., Северюхин А.В., Северюхина О.Ю. Расчет макрохарактеристик наносистем. Часть 2. Коэффициент теплопроводности многокомпонентных наносистем // Химическая физика и мезоскопия. – 2017. – Т. 19, № 4. – С. 538–546.
- Green M.S. Markoff Random Processes and the Statistical Mechanics of Time-Dependent Phenomena. II. Irreversible Processes in Fluids // J. Chem. Phys. – 1954. – Vol. 22. – P. 398–413.
- Kubo R., Yokota M. and Nakajima S. Statistical-Mechanical Theory of Irreversible Processes. II. Response to Thermal Disturbance // J. Phys. Soc. Jpn. – 1957. – Vol. 12. – P. 1203–1211.
- Green M.S. Markoff Random Processes and the Statistical Mechanics of Time-Dependent Phenomena. II. Irreversible Processes in Fluids // J. Chem. Phys. – 1954. – Vol. 22. – P. 398–413.
- Mori H. Statistical-Mechanical Theory of Transport in Fluids // Phys. Rev. – 1958. – Vol. 112. – P. 1829–1842.
- Green M.S. Comment on a Paper of Mori on Time-Correlation Expressions for Transport Properties // Phys. Rev. – 1960. – Vol. 119. – P. 829–830.
- Kadanoff L.P. and Martin P.C. Hydrodynamic equations and correlation functions // Annals of Physics. – 1963. – Vol. 24. – P. 419–469.
- Luttinger J.M. Theory of Thermal Transport Coefficients // Phys. Rev. – 1964. – Vol. 135. – P. A1505–A1514.
- Visscher W.M. Transport processes in solids and linearresponse theory // Phys. Rev. A. – 1974. – Vol. 10. – P. 2461–2472.
- Lepri S., Livi R. and Politi A. Thermal conduction in classical low-dimensional lattices // Phys. Rep. – 2003. – Vol. 377. – P. 1–80. DOI: 10.1016/S0370-1573(02)00558-6
- Kundu A., Dhar A. and Narayan O. The Green–Kubo formula for heat conduction in open systems // J. Stat. Mech. – 2009. – I. 3. – L03001. – P. 1–4. DOI: 10.1088/1742-5468/2009/03/L03001
- Allen K.R. and Ford J. Lattice Thermal Conductivity for a One-Dimensional, Harmonic, Isotopically Disordered Crystal // Phys. Rev. – 1968. – Vol. 176. – P. 1046–1055.
- Fisher D.S. and Lee P.A. Relation between conductivity and transmission matrix // Phys. Rev. B. – 1981. – Vol. 23, № 12. – P. 6851–6854.
- Allen K.R. and Ford J. Lattice Thermal Conductivity for a One-Dimensional, Harmonic, Isotopically Disordered Crystal // Phys. Rev. – 1968. – Vol. 176. – P. 1046–1055.
- Fisher D. S. and Lee P. A. Relation between conductivity and transmission matrix // Phys. Rev. B. – 1981. – Vol. 23, № 12 – P. 6851–6854.
- Lammps [Электронный ресурс]. – URL: http://lammps.sandia.gov/doc/compute_heat_flux.html (дата обращения 07.09.2020).
- Simulation of the processes of formation of quantum dots on the basis of the transition metals / A.V. Vakhrushev, O.Yu. Severyukhina, A.V. Severyukhin [et al.] // Nanomechanics Sci. Tech. Int. J. – 2012. – Vol. 3. – P. 51–75. DOI: 10.1615/NanomechanicsSciTechnolIntJ.v3.i1.30
- Howell Р.С. Comparison of molecular dynamics methods and interatomic potentials for calculating the thermal conductivity of silicon // The Journal of Chemical Physics. – 2012. – Vol. 137. – Р. 224111.
- Теплофизические свойства компонентов горючих систем / Ю.Е. Шелудяк, Л.Я. Кашпоров, Л.А. Малинин, В.Н. Цал-ков. – М.: НПО, 1992. – 184 с.


