РАСЧЕТ КОЛИЧЕСТВА АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ ДЛЯ ПОИСКА ОБРАТНОЙ МАТРИЦЫ И ПОВЫШЕНИЯ НАДЕЖНОСТИ ПРИНЯТЫХ СИМВОЛОВ В АЛГОРИТМЕ ПЕРЕСТАНОВОЧНОГО ДЕКОДИРОВАНИЯ НА ПРИМЕРЕ КОДА ХЭММИНГА (7, 4, 3)

На сегодняшний день активно развиваются системы дистанционного управления, передачи команд управления в реальном времени, машинного обучения, роботизированные системы, и т.д. Применяемые в подобных сетях радиоканалы требуют защиты передаваемых по ним данных от ошибок и влияния внешних деструктивных факторов – попыток перехвата сигнала, срывов процедуры управления [1–4]. Эффективным средством защиты радиоканалов является применение средств перестановочного декодирования (ПД). К тому же, ПД является средством повышения энергетической эффективности систем связи, что является одним из основных направлений развития телекоммуникационных систем.

В связи с отсутствием в цифровой информации избыточности, искажение любого переданного символа приводит к потере достоверности данных. В системах управления фактор достоверности является решающим – в качестве управляющих команд могут выступать исключительно достоверные данные. Теория помехоустойчивого кодирования является мощным средством повышения энергетической эффективности систем связи за счет рационального введения в цифровые данные избыточности [5–9]. Использование классического варианта алгоритма ПД позволяет в значительной мере повысить энергетическую эффективность систем связи, однако, алгоритм содержит этапы,

выполнение которых приводит к временным задержкам, что является существенным недостатком в системах передачи команд управления.

Таким образом, снижение вычислительных затрат приведет к еще большему повышению энергетической эффективности систем связи, а также к значительному временному выигрышу и ускорению работы алгоритмов. Полученные результаты ускорения и снижения затрат алгоритма декодирования востребованы в самых популярных областях – системах дистанционного управления беспилотными летательными аппаратами (БПЛА) различного типа, высокоскоростных оптических линиях связи, работающих с упреждающей коррекцией ошибок в условиях применения сложных видов модуляции и т.д. Описанного результата удается достичь путем применения когнитивной карты декодера (ККД) [10–12], что хранит множество необходимых для вычисления параметров эквивалентного кода (ЭК) матриц, соответствующих ряду возможных ситуаций, что обеспечивает временной выигрыш при реализации перестановочного декодирования за счет ухода от матричных преобразований в процессе выполнения процедуры декодирования.

Алгоритм перестановочного декодирования без применения когнитивной карты декодера

Классический алгоритм перестановочного декодирования описан в работах [13–15]. Вычисления реализуются по 12-ти шагам.

Шаг 1. Принятие поступающих из канала связи битов и фиксация жестких решений вектора приема V _пр ,на который в канале связи действует вектор ошибок V _е . Каждый соответствующий бит сопровождается оценкой надежности принятия символа λ с помощью значений МРС (мягких решений символов).

Шаг 2. Ранжирование значений МРС в порядке убывания. Слева записываются наиболее надежные символы с высоким значением λ. Данный способ расположения наиболее надежных символов связан с размещением слева единичной матрицы, входящей в состав порождающей матрицы в систематической форме для групповых кодов.

Шаг 3. После выполнения ранжирования символов в соответствии с убыванием МРС произведение биективных преобразований вида f : V ° ^— У. , где V пер - переставленный вектор. На этом шаге также происходит формирование соответствующей биекции матрицы перестановок P .

Шаг 4. Фиксирование в виде информационного вектора V ' _инф выделенных в векторе V пер левых k наиболее надежных символов.

Шаг 5. Осуществление вычисления переставленной матрицы G' путем умножения порождающей матрицы исходного кода G на матрицу перестановок P (G х P) .

Шаг 6. Выделение левых k столбцов переставленной матрицы G' для получения ключевой матрицы Q размерности k х k . Вычисление определителя матрицы Q - А . Если А ^ 0, переходим к шагу 7. Если А = 0, отказываемся от декодирования и переходим к шагу 2 с выполнением новых перестановок, меняя местами символы с номером k с символом с номером k + 1. Таким же образом происходит трансформирование матрицы перестановок P .

Шаг 7. Вычисление матрицы миноров M Q для ключевой матрицы Q.

Шаг 8. Нахождение обратной матрицы Q -1. Для этого элементы матрицы Q T необходимо разделить на значение А .

Шаг 9. Приведение переставленной матрицы G' к систематическому виду G ¹_cucm с использованием полученной обратной матрицы Q -1.

Шаг 10. Вычисление вектора эквивалентного кода V _экв путем умножения нового информационного вектора V¹_инф , полученного в ходе проведения процедур четвертого шага, на матрицу G ¹_cucm .

Шаг 11. Умножение вектора эквивалентного кода V э_кв на транспонированную матрицу перестановок P ^т. После этого осуществляется нахождение обратной биекции f : V ~° — V и получается эквивалентный переставленный вектор V °°p_p .

Шаг 12. Поразрядное сложение векторов V пр и V °' для вычисления вектора V e , характеризующего воздействие ошибок в канале связи во время фиксации битов вектора V пр .

Видно, что наиболее затратными в энергетическом и временном плане являются шаги 6-8, на которых осуществляется вычисление определителя ключевой матрицы и нахождение ее обратной матрицы. Далее будет выполнен расчет количества простейших арифметических операций для худшего случая.

Поиск обратной матрицы для нахождения эквивалентного кода

Рассмотрим 6-8 шаги декодирования кода Хэмминга (7, 4, 3). Подсчитаем количество элементарных операций, необходимых для нахождения определителя и обратной матрицы. Ключевая матрица кода Хэмминга (7, 4, 3) имеет формат (4 х 4).

Находим определитель матрицы А:

^ a b c d^Л

Л е f g h

A =                 .

i j k l

₄ m n o p_;

В качестве примера разложим операцию вычисления определителя матрицы методом разложения по первой строке на простые арифметические операции.

( a b c d \

det( A )

e

= a х ( - 1)^{1 + 1} х j

+ n х ( - 1)^{1 + 3} х

1^{1 + 1} х

k

o

х| e х ( - 1)¹⁺¹ х

k

o

g

k

^ ^m h У

f ^j n

g

o

h

P J

I ⁿ

e

i

^ m

l

P

l

P

o

f ^j n

: l + b х ( - 1)

’ P j

' h У l + d х (-1)' p J

= a х ( - 1)¹⁺¹ х

+ g х ( - 1)^{1 + 2} х

1^{1 + 2} х

( e i

g

k

h У l

+

1^{1 + 4} х

j I n p

+ b х ( - 1)^{1 + 2} х

+ g х ( - 1)^{1 + 2} х

i l

m p

+ c х ( - 1)^{1 + 3} х

^ m ^ e

i

m

o

f ^j n

P J

g k

o

1^{1 + 3} х

1^{1 + 3} х

j

n

k

o

+

J

i

k

+

m

o

J

х| _е х ( - 1)^{1 + 1} х

j

l

n

p

+ f х ( - 1)^{1 +} 2 х

il

mp

+ d х ( - 1)¹⁺⁴ х

+ h х ( - 1)^{1 + 3} х

ij

m

n

+

х| e х ( - 1)^{1 + 1} х j х k + f х ( - 1)^{1 +} 2 х — х- + g х ( - 1)^{1 + 3} х — х j V       no       mo       m n

= a х ( - 1)^{1 + 1} х ( f х ( - 1)^{1 + 1} х ( k х p - 1 х o ) +

+ g х ( - 1)¹⁺² х ( j х p - 1 х n ) + h х ( - 1)^{1 + 3} х ( j х o - k х n ) ) + + b х ( - 1)¹⁺² х ( e х ( - 1)^{1 + 1} х ( k х p - 1 х o ) +

+ g х ( - 1)^{1 + 2} х ( i х p - 1 х m ) + h х ( - 1)^{1 + 3} х ( i х o - k х m ) ) + + c х ( - 1)^{1 + 3} х ( e х ( - 1)^{1 + 1} х ( j х p - 1 х n ) +

+ f х ( - 1)^{1 + 2} х ( i х p - 1 х m ) + h х ( - 1)^{1 + 3} х ( i х n - j х m ) ) + + d х ( - 1)^{1 + 4} х ( e х ( - 1)^{1 + 1} х ( j х o - k х n )

+ f х ( - 1)^{1 +} 2 х ( i х o - k х m ) + g х ( - 1)^{1 + 3} х ( i х n - j х m ) ) = = 111 операций.

При подсчете числа операций следует учитывать, что по времени исполнения и сложности операции умножения и сложения считаются равными, поскольку умножаются целые числа. Операция умножения на 0 учитывается, поскольку она также выполняется процессором.

Для выполнения операции вычисления определителя матрицы потребуется выполнить 111 элементарных арифметический операций.

Находим обратную матрицу А ^-1 . В случаях, когда det( A ) ^ 0, обратная матрица для матрицы А существует. Находим обратную матрицу с использованием матрицы алгебраических дополнений.

A-1	=    1 = det( A ) х		C T =
	Г C 11	с 21	C 31	C 41 ^
1 х	C 12	22	32	C 42
det( A )	C 13	23	33	C 43
	V C 14	с 24	Си 34	с 44 >

где С – союзная матрица для матрицы А.

Приступаем к нахождению алгебраического

дополнения для последующего вычисления со-

юзной матрицы С:

+ C 42 X ( - 1) (¹⁺³⁾

с

= ( - 1) ( ^{l + 1)} x ( C 22 X ( - 1) ( ^{l + 1)} X ( C ₃₃ X C 44 - C 34 X C 43 ) +

+ C 32 X ( - 1) 3 x ( C 23 X C 44 - C 24 X C 43 ) + + C 42 X ( - 1) ^{1 + 3} X ( C 23 X C 34 - C 24 X C 33 ) ) .

Для вычисления одного элемента матрицы С необходимо вычислить алгебраическое дополнение (3 х 3), выполнив 23 операции. Всего необходимо найти 16 элементов матрицы С, для чего потребуется выполнить 368 операций. Для последнего действия – нахождения обратной матрицы – необходимо умножить союзную матрицу на 1/det( A ), для чего потребуется выполнить 17 операций (деление и умножение каждого из 16 элементов на полученное значение).

Для проведения матричных вычислений классического алгоритма перестановочного декодирования кода Хэмминга (7, 4, 3) с шестого по восьмой шаг было выполнено 111+368+17=496 арифметических операций. При этом извлечение готового результата из априори созданной ККД потребует выполнения всего 3 элементарных операций, которые не связаны с арифметическими действиями. Это способствует ускорению процесса обработки цифровых данных в высокоскоростных системах обмена информацией.

C 11 = ( - 1) ^{1 + 1} X

к ^24

C ⁴²'

C ⁴³

с

^ 44 7

= ( - 1) ^{(1 + 1)} xl C 22 X ( - 1) ^{(1 + 1)} X

+ C 32 X ( - 1) ^{(1 + 2)} X

С

С

+

+

Выигрыш в арифметических операциях при внедрении когнитивной карты декодера

Для сравнения эффективности работы классического алгоритма ПД и алгоритма ПД с ККД, следует сравнить число арифметических операций, необходимых для выполнения матричных преобразований с числом операций перебора внутри ККД.

В работе [14] было установлено, что полное множество комбинаций перестановок для кода Хэмминга (7, 4, 3) включает 35 комбинаций, 20 % из которых приводят к получению нулевого определителя и являются непродуктивными. В случае выпадения непродуктивной перестановки, вместо 111 операций, необходимых для вычисления определителя матрицы, будет выполнено сравнение всего с 7-ю комбинациями, что эквивалентно 7 арифметическим операциям. В случае получения продуктивной перестановки, будет выполнено сравнение с 7-ю непродуктивными перестановками и получен допуск к блоку продуктивных перестановок, где в худшем случае будет выполнено 28 операций сравнения вместо 496 арифметических операций.

Таким образом, выигрыш по количеству элементарных операций составит более 90 %.

Повышение надежности переданных по каналу связи символов с использованием алгоритма Бала

При выполнении процедуры декодирования, отсутствует гарантия наличия достаточно надежных символов для получения ЭК, ввиду чего становится невозможным применение узкого набора перестановок для получения ЭК. Алгоритм Бала – готовое решение повышения надежности символов –можно рассматривать в качестве выбора, как альтернативного поиску новой перестановки.

Алгоритм Бала описывается выражением:

L ( d 1 ) Ш L ( d 2 ) - L ( d 1 © d 2 ) -

- ( - 1) x sign[ L ( d i )] x sign[ L ( d 2 )] x min {| L ( d 1 )| , | L ( d 2 )| } , где обозначение Ш символизирует действие, представленное нижней строкой формулы;

L(d₁) – стратегически независимые информационные биты;

L(d₂) – биты четности от сочетаний L(d₁) .

Для осуществления алгоритма Бала требуется определенная подготовка: во время приема кодового вектора, вместе с выработкой МРС также следует провести операцию проверки на четность. В свою очередь, для проверки проверочных символов на четность требуется искусственно ввести надежный проверочный символ h ₄ . Код Хэмминга (7, 4, 3) можно представить на рассмотрение в следующем виде: x ₁ x ₂ x ₃ x ₄ h ₁ h ₂ h ₃ h ₄, а проверки на четность описываются выражениями: h ₁ + h ₂ + h ₃ = h 4 , x ₁ + x ₂ + x ₃ = h ₁, x ₂ + x 3 + x ₄ = h ₂, x ₁ + x ₂ + x ₄ = h 3 , что показано на рисунке 1.

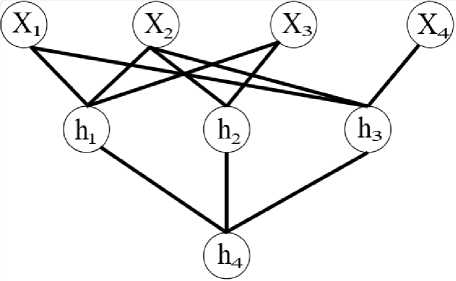
Рисунок 1. Проверка на четность элементов кодового вектора

Декодер со встроенным алгоритмом Бала работает следующим образом. После выработки МРС и первичной проверки на четность информационных символов x1x2x3x4 происходит повышение степени их надежности при выполнении алгоритма Бала. После первичного применения алгоритма повышения степени надежности символов к информационным разрядам происходит проверка избыточных символов h1h2h3 с последующим применением к ним алгоритма Бала в случае, если их МРС принимает значение, отличное от максимального, восстанавливая комбинациями x1x2x3h1, x2x3x4h2 или x1x2x4h3 надежность избыточных символов. Любые изменения МРС для каждого символа записывают в общий кодовый вектор VMPC. После того, как вектор выполнит все необходимые проверки и восстанавливающие процедуры, формируется вектор более надежных символов. Это позволяет выбрать подходящую комбинацию перестановок.

Экспериментальным путем было подтверждено, что в некоторых ситуациях выполнение алгоритма Бала до конца не является оптимальным решением. В частности, можно сократить время, затрачиваемое на выполнение алгоритма, если знаки символов, полученных на первом шаге, будут идентичны знакам исходных символов.

Операция повышения степени надежности позволит формировать ККД с минимально возможным количеством перестановок – от одной до k x ( n - k - 1) перестановок, благодаря чему объем занимаемой памяти позволит хранить готовые матрицы (проверочная, транспонированная), соответствующие каждой хранимой перестановке.

Расчет количества арифметических операций, необходимых для выполнения алгоритма повышения надежности

Подготовительными операциями являются операции проверки на четность hj + h2 + h3 = h4, x1 + x 2 + x3 = h1, x 2 + x3 + x4 = h2, x1 + x 2 + x4 = h3 и для их выполнения потребуется 8 арифметических операций. При возникновении ошибки при проверке на четность начинается выполнение алгоритма Бала. Для расчета повышения степени надежности во внимание принимается значение максимальной оценки МРС x1 + x2 + x4 = h3 и 2 оценки символов - Aa и Ab. Формируется список повышающих степень надежности коэффициентов (для Aa и Ab соответственно). Значение оценки Aa следует сложить с повышающим коэффициентом, полученном на предыдущем шаге для Ab и умножить на -1. При отрицательном значении полученного коэффициента или исходного значения x1 + x2 + x4 = h3 повторить процедуру умножения на -1. Соответствующие действия выполняются для оценки Ab. Поскольку алгоритм Бала выполняется до тех пор, пока дважды не будут получены идентичные значения восстановления символов, следует вычислить арифметиче- скую сложность выполнения 1 шага восстановления: от 4 до 6 простых арифметических операций. Поскольку во внимание следует принимать расчеты на худший случай – примем в расчет 6 элементарных арифметических операций.

Количество шагов для достижения конечного повышения может быть не достигнуто в принципе, поэтому на практике следует устанавливать ограничение по количеству выполненных шагов повышения степени надежности. Максимальное количество повторений шага восстановления символов без наличия результата (в случае отсутствия остановки) можно рассчитать по формуле размещения с повторениями для величины множества оценок МРС, в том числе и с отрицательным знаком, что для кода Хэмминга (7, 4, 3) составляет 15² = 225 шагов и 1350 арифметических операций. Данный расчет показывает необходимость введения ограничений на восстанавливающие операции, иначе они теряют актуальность в связи с продолжительностью своего исполнения. На практике большинство восстановлений происходят менее чем за n шагов, в связи с этим может быть введена рекомендация об ограничении количества исполняемых циклов до 2n шагов, что потребует выполнения не более 90 простейших арифметических операций.

Таким образом, алгоритм восстановления символов за 90 простейших арифметических операций способен повысить достоверность переданных данных, а значит, разрешить применение большего числа перестановок для выполнения процедуры ПД. Это означает, что объем ККД может быть во многом сокращен и вмещать порядка n перестановок, к выбору которых можно будет прийти с применением алгоритма восстановления символов.

Заключение

В статье была доказана необходимость применения ККД и рассмотрен восстанавливающий переданные символы алгоритм Бала. Применение ККД позволяет существенно сократить количество арифметических операций при вычислении параметров ЭК, а значит упростить данную операцию, обеспечив при этом временной и энергетический выигрыш при реализации перестановочного декодирования. Алгоритм восстановления символов, в свою очередь, позволяет существенно сократить объем ККД и сводить алгоритм ПД к применению ряда хранимых комбинаций. Совмещение рассмотренных средств упрощения алгоритма ПД приведет к уменьшению объема ККД и сокращению времени на исполнение декодирования.