Расчет композитных цилиндрических оболочек с применением многосеточных элементов
Автор: Матвеев А.Д., Гришанов А.Н.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 3 т.17, 2016 года.
Бесплатный доступ
Предложена процедура расчета трехмерных упругих композитных цилиндрических оболочек с различными коэффициентами наполнения, которая сводится к построению дискретных моделей, состоящих из криволинейных сложных многосеточных конечных элементов. В основе построения таких элементов лежат криволинейные двухсеточные конечные элементы. Двухсеточные и сложные многосеточные элементы проектируются на основе базовых конечно-элементных моделей композитных оболочек, которые учитывают их неоднородную структуру и имеют высокую размерность. Показаны процедуры построения в локальных декартовых системах координат криволинейных двухсеточных и сложных многосеточных элементов. Поля перемещений аппроксимируются известными степенными полиномами различных порядков, напряженное состояние описывается уравнениями трехмерной задачи теории упругости (без введения упрощающих гипотез о характере распределения полей перемещений, деформаций и напряжении). Аппроксимирующие полиномы и уравнения трехмерной задачи упругости записываются в локальных декартовых системах координат. Достоинства предлагаемых элементов состоят в том, что они описывают трехмерное напряженное состояние в композитных оболочках, учитывают их неоднородные структуры, сложное закрепление и порождают многосеточные дискретные модели с малым числом узловых неизвестных. Размерности многосеточных дискретных моделей оболочек на несколько порядков меньше размерностей базовых моделей. Временные затраты реализации метода конечных элементов (МКЭ) на ЭВМ для многосеточных дискретных моделей композитных оболочек существенно меньше, чем для базовых моделей. Предложен сложный многосеточный элемент 3-го порядка для расчета композитных цилиндрических оболочек. Приведен пример расчета по МКЭ консольной трехслойной оболочки с использованием сложных многосеточных элементов 3-го порядка. Результаты расчетов оболочки показывают высокую эффективность применения предложенных сложных элементов.
Композиты, упругость, цилиндрические оболочки, метод конечных элементов, криволинейные сложные многосеточные конечные элементы
Короткий адрес: https://sciup.org/148177598
IDR: 148177598 | УДК: 539.3
Текст научной статьи Расчет композитных цилиндрических оболочек с применением многосеточных элементов
Введение. Цилиндрические композитные (многослойные) оболочки широко применяются на практике, особенно в авиационной и космической технике. При расчетах композитных оболочек на прочность используют различные теории [1–4]. В основе существующих теорий оболочек лежат гипотезы, которые накладывают определенные ограничения на поля перемещений, деформаций и напряжений, существенно искажают реальные распределения напряжений в окрестностях закреплений оболочек или при действии локальных нагружений и порождают решения с неустранимой погрешностью. Чтобы избежать этих трудностей, необходимо решать проблему расчета оболочек в рамках трехмерной задачи теории упругости.
Как известно [5], расчет на прочность конструкции сводится к нахождению ее коэффициента запаса, который определяется с помощью максимального эквивалентного напряжения. Использование метода конечных элементов (МКЭ) при расчетах на прочность трехмерных композитных оболочек связано с большими трудностями [6–8]. При нахождении максимальных эквивалентных напряжений с малой погрешностью необходимо использовать достаточно мелкие разбиения, которые учитывают неоднородную (микронеоднородную) структуру оболочек, сложный вид их крепления и нагружения. Это порождает дискретные модели композитных оболочек очень высокой размерности и, как следствие, большую вычислительную погрешность. Таким образом, возникает необходимость в разработке новых конечных элементов (КЭ) и алгоритмов расчетов, более эффективных, чем существующие, которые сочетают в себе достоинства МКЭ и просто реализуются в расчетах напряженного деформированного состояния (НДС) конструкций со сложной неоднородной структурой.
В данной работе показано многосеточное моделирование трехмерных линейно-упругих композитных цилиндрических оболочек с различными коэффициентами наполнения. Предлагаемое моделирование сводится к построению дискретных моделей оболочек, которые состоят из криволинейных сложных многосеточных конечных элементов (МнКЭ). При проектировании сложного МнКЭ используется конечное число двухсеточных конечных элементов (ДвКЭ), которые представляют область сложного МнКЭ. Показаны процедуры построения в локальных декартовых системах координат криволинейных
ДвКЭ и сложных МнКЭ. Двухсеточные и сложные многосеточные элементы формы прямоугольного параллелепипеда (прямоугольника, треугольника) для анализа деформирования трехмерных (двумерных) упругих тел неоднородной структуры рассмотрены в работах [9–11]. В ДвКЭ и сложных МнКЭ функции перемещений интерполируются многочленами в форме степенных полиномов различных порядков [6–8], напряженное деформированное состояние описывается уравнениями трехмерной задачи теории упругости [12], которые записываются в локальных декартовых системах координат. В процедурах построения криволинейных ДвКЭ и сложных МнКЭ не требуется определять функции, которые связывают декартовые координаты с локальными криволинейными, и вычислять матрицу Якоби, что необходимо выполнять в существующих процедурах построения криволинейных КЭ [6–8].
При построении сложного МнКЭ используется криволинейная мелкая сетка (высокой размерности) и крупные сетки (малой размерности), вложенные в мелкую, на которых определяются аппроксимирующие функции перемещений. Базовое разбиение сложного элемента, которое учитывает его неоднородную структуру, порождает мелкую сетку. На базовом разбиении строится матричное выражение функционала полной потенциальной энергии сложного МнКЭ, в котором узловые перемещения мелкой сетки представляются через узловые перемещения крупных сеток. В результате полученное матричное выражение функционала энергии имеет малую размерность. Минимизируя построенный функционал, получаем формулы вычисления матрицы жесткости и вектора узловых сил сложного МнКЭ.
Приведен пример расчета трехслойной цилиндрической оболочки с применением сложных МнКЭ 3-го порядка. При построении ДвКЭ используются криволинейные однородные односеточные КЭ 1-го порядка, построенные в локальных декартовых системах координат.
1 . Однородные криволинейные односеточные КЭ
Кратко рассмотрим процедуру построения криволинейных КЭ 1-го порядка в локальных декартовых системах координат (более подробно изложена в работах [13–15]). На рис. 1 показан криволинейный односеточный КЭ Ve 1-го порядка с характерными размерами he х hy х he, где ae - угол раствора КЭ Ve; O1 x1 y1 z1 - локальная декартова система координат; z1 O1 y1 - плоскость симметрии; cd - ось цилиндрической оболочки; Re , Re - радиусы нижней и верхней поверхностей конечного элемента Ve; he - толщина, he - длина КЭ V, he = a„Re; узлы отмечены точка-y exe ми и пронумерованы (8 узлов). Итак, форма КЭ Ve есть прямая призма высотой hye , основанием которой является криволинейный четырехугольник 1-3-4-2. Конечный элемент Ve рассматриваем как тело, которое испытывает трехмерное напряженное состояние и для которого перемещения, деформации и напряжения удовлетворяют соотношениям Коши и закону Гука трехмерной задачи теории упругости [12]. Для мелких разбиений угол раствора ae КЭ Ve мал. Тогда формы КЭ Ve и прямоугольного параллелепипеда мало отличаются. Поэтому для аппроксимации функций перемещений ue, ve, we элемента Ve используем полиномы 1-го порядка, записанные в локальной декартовой системе координат O1 x1 y1 z1 (рис. 1). Функцию перемещений ue (ve, we) представим в виде ue = a1 + a 2 x1 + a 3 y1 + a 4 z1 + a 5 x1 y1 + + a 6 z1 x1 + a 7 z1 y1 + a 8 x1 y 1 z1.
Используя представления вида (1), по алгоритмам МКЭ строим аппроксимирующие функции перемещений ue , ve , we для КЭ Ve , которые применяем в виде [7; 8]
8 8 8
u e = L Niu1’ v e = Z Nv1’ w e = E N i w 1, (2) i = 1 i = 1 i = 1
где u i , v1 , w i 1 - перемещения i -го узла; u i 1 ( v i 1, w i 1) -перемещение i -го узла КЭ Ve в направлении оси O 1 x 1 ( O 1 y 1 , O 1 z 1 ); N i = N i ( x 1 , y 1 , z 1 ) - функция формы i -го узла КЭ Ve .
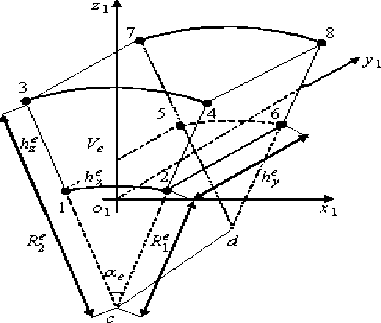
Рис. 1. КЭ Ve 1-го порядка
Полную потенциальную энергию W e ( § e ) для КЭ Ve запишем в матричной форме [7; 8]:
W e ( ^ e ) = ^jX ) T [ B e ] T [ D e ][ B e ] 6 e dV —
-
2 V
Ve
-
- J ( 6 e ) T [ N e ] T F e dV — J ( 6 e ) T [ N e ] T q e dS , (3)
VeSe где [Be ], [De ] - матрицы деформаций и модулей упругости КЭ Ve; 6e, - вектор узловых перемещений КЭ Ve, имеющий (в системе координат O1 x1 y1 z1) следующую структуру:
-
6 e = { u 1 ,..., u N , v 1 ,..., v N , w 1 ,..., w N } , (4)
где N - число узлов КЭ Ve (для рис. 1 имеем N = 8).
Применяя принцип минимума потенциальной энергии [8] для КЭ Ve , т. е. выполняя условие 5We ( ^ e )/ 5 6 e = 0, получаем соотношение [ K e ] 6 e = P e , где
[ K e ] = J [ B e ] T [ D e ][ B e ] dV ,
V e
P e 1 = J [ N e ] T F e dV + J [ N e f q e dS , (5)
VeSe где [Ke] - матрица жесткости; Pe - вектор узловых сил КЭ Ve , которые определяются в локальной декартовой системе координат O1 x1 y1 z1 КЭ Ve.
Учитывая (5), выражение полной потенциальной энергии We ( 6 e ) представим в виде
W e ( 6 e ) = 2( 6 e ) T [ K e ] » e - ( » e ) T p e . (6)
Криволинейность области КЭ Ve учитывается в формулах (5). Далее выражения полных потенциальных энергий криволинейных композитных ДвКЭ и сложных МнКЭ для удобства изложения будем записывать в форме, аналогичной (6). Процедуры построения однородных криволинейных односеточных КЭ 2-го, 3-го порядка, которые геометрически подобны форме КЭ Ve (рис. 1), аналогичны вышеописанной. Здесь рассматриваем композитные криволинейные ДвКЭ и сложные МнКЭ, геометрически подобные форме КЭ Ve (рис. 1).
2. Композитные криволинейные ДвКЭ
Рассмотрим две процедуры построения трехмерных криволинейных ДвКЭ с неоднородной структурой на примере ДвКЭ Va ( V b ) 3-го порядка с характерными размерами h X^ х h ya х hz “ (рис. 2, где Oxyz -локальная декартова система координат; hza - толщина и hya - длина ДвКЭ Va ).
Пусть между компонентами неоднородной структуры ДвКЭ Va связи идеальны. Компоненты есть линейно-упругие однородные тела, перемещения, деформации и напряжения которых удовлетворяют соотношениям Коши и закону Гука трехмерной задачи теории упругости [12]. Базовая дискретная модель (базовое разбиение) Ra ДвКЭ Va состоит из однородных криволинейных КЭ Ve 1-го порядка с характерными размерами h e х h y х h e (см. рис. 1). Дискрет -ная модель Ra учитывает неоднородную структуру ДвКЭ Va и порождает мелкую сетку ha . Отметим, что дискретные модели Ra всех ДвКЭ Va образуют базовую дискретную модель оболочки. Считаем, что h e , h e , a e = const, где e = 1, ..., M ; M - общее число КЭ Ve (см. рис. 1). На мелкой сетке ha определяем крупную сетку Ha ДвКЭ Va . Узлы сетки Ha (32 узла), отмеченные на рис. 2 точками, равномерно расположены на ребрах ДвКЭ Va (по 4 узла на каждом ребре). Порядок ДвКЭ определяется порядком интерполяционного полинома, который построен на его крупной сетке. Считаем, что угол раствора a a ДвКЭ V a мал. Тогда криволинейная форма ДвКЭ Va мало отличается от формы прямоугольного параллелепипеда. Поэтому при построении функции перемещений на крупной сетке Ha ДвКЭ Va используем известные интерполяционные полиномы 1-го, 2-го и 3-го порядка [7; 8], записанные в локальной декартовой системе координат Oxyz . В связи с этим, ДвКЭ Va будем называть ДвКЭ соответственно 1-го, 2-го и 3-го порядка.
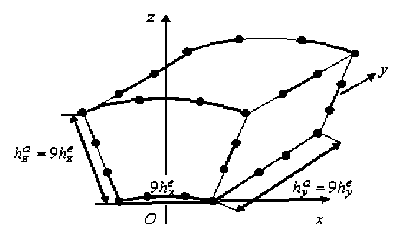
Рис. 2. ДвКЭ V a ( V b )
-
2.1. Первая процедура построения ДвКЭ. Первую процедуру (не теряя общности суждений) рассмотрим на примере построения ДвКЭ Va 3-го порядка (рис. 2). На крупной сетке Ha строим аппроксимирующие функции перемещений ua , va , wa ДвКЭ Va , используя полиномы 3-го порядка, записанные в системе координат Oxyz . Для функции ua имеем
u a = a 1 + a 2 x + a 3 y + a 4 z + a 5 xy + a 6 zx + a 7 zy + a8 xyz + 2222 2 2
+ a 9 x + a 10 y + a 11 z + a 12 xy + a 13 xz + a 14 yx +
+ а 15 y 2 z + a 16 z 2 x + a 17 z 2 y +
з . з . з . з . з . з .
+ a 18 x + a 19 y + a 20 z + a 21 xy + a 22 xz + a 23 yx +
з з 3 2 2
+ a 24 y z + a 25 z x + a 26 z y + a 27 x yz + a 28 y xz +
2333 + a 29 z xy + a 30 x yz + a 31 y xz + a 32 z xy .
Функции перемещений ua , va , wa , построенные по МКЭ, запишем в форме [7]
n 0 n 0 n 0
U a = Z N в q в , V a = £ N e q vv , W a = £ N ₽ q w , (7) i = 1 i = 1 i = 1
где q U , q V , qw7 , N B - перемещения и функция формы в—го узла сетки Ha , в = 1, ..., n 0; n 0 - общее число узлов сетки Ha (для ДвКЭ 3-го порядка n 0 = 32).
Обозначим 6 a = { q u , ..., q u 2, q v , ..., q 32 , q w , ..., q w } -вектор узловых перемещений крупной сетки Ha , т. е. ДвКЭ Va . Пусть ось O 1 y 1 КЭ Ve (см. рис. 1), который расположен в базовой модели ДвКЭ Va , параллельна оси Oy (см. рис. 2) и между осями O 1 x 1 и Ox угол равен в e . Вектор 6 e узловых перемещений КЭ Ve , отвечающий системе координат Oxyz , имеет вид
-
6 e = u ,..., u e , v e ,..., v e , w e ,..., w e } T , (8)
где uie , vie , wie – перемещения узла i КЭ Ve , i = 1, ..., 8.
Между векторами δ 1 e , δ e КЭ Ve (см. п. 1) имеем связь 6 e = [ T e ] 6 e , где [ T e ] - матрица вращений (размерности 24 х 24), которая в силу (4), (8) имеет вид [8]
[Те ] =
[ E 1 ]
[ E 0 ]
— [ E 2 ]
[ E 0 ][ E 2 ]
[ E ] [ E 0 ]
[ E 0 ][ E 1 ]
где [ E 0], _.,[ E 2] - матрицы размерности 8 х 8; [ E 0] -нулевая и [ E ] - единичная матрицы; [ E 1 ] = cos в e [ E ]; [ E 2 ] = sin в e [ E ].
Подставляя 6 e = [ Te ] 6 e в (6) и выполняя условие d We ( 6 e ) / d 6 e = 0 , получаем соотношение [ Ke ] 6 e = F e , где [ Ke ]– матрица жесткости и P e – вектор узловых сил КЭ Ve , определяемые в декартовой системе координат Oxyz (рис. 2) по формулам
-
[ Ke ] = [Te ]T [ K1][ Te ], Pe = [Te ]T Be* .(10)
Выражение полной потенциальной энергии Wa для ДвКЭ Va запишем в матричной форме
M
Wa =Zk6[KKe ] 6e — 6e^e(11)
-
e=1 V 2
-
2.1.1. Процедура определения напряжений в ДвКЭ V a . Пусть найден вектор δ a узловых перемещений ДвКЭ Va в локальной декартовой системе координат Oxyz (см. рис. 2). По формуле (12) находим (в декартовой системе координат Oxyz ) вектор δ e узловых перемещений КЭ Ve , e = 1, ..., M . Определяем вектор δ 1 е узловых перемещений КЭ Ve в локальной декартовой системе координат O 1 x 1 y 1 z 1 (см. рис. 1) по формуле 6 e = [ Te ] 6 e , e = 1, ..., M . Используя вектор δ 1 е , функции перемещений КЭ Ve , по алгоритмам МКЭ находим функции напряжений в каждом КЭ Ve базового разбиения ДвКЭ Va . Это позволяет определять напряжения в любом компоненте неоднородной структуры ДвКЭ Va .
-
2.2. Вторая процедура построения ДвКЭ. Основные положения 2-й процедуры рассмотрим на примере построения криволинейного ДвКЭ Vb 3-го порядка, который имеет размеры, геометрическую форму, неоднородную структуру и расположен в локальной декартовой системе координат Oxyz , как ДвКЭ Va (рис. 3). В данной процедуре используем мелкую ha и крупную Ha сетки, базовое разбиение Ra и функции перемещений ua , va , wa (см. формулу (9)) ДвКЭ Va , т. е. δ a есть вектор узловых перемещений ДвКЭ Vb . На базовом разбиении Ra ДвКЭ Vb с помощью метода конденсации [8] строим суперэлемент Gbs , полную потенциальную энергию Ws которого запишем в матричной форме:
Используя функции (7), узловые перемещения вектора δ e КЭ Ve выражаем через узловые перемещения крупной сетки Ha , т. е. вектора δ a ДвКЭ Va . В результате получим равенство
6 e = [ A a ] 6 а , (12)
где [ Aea ] – прямоугольная матрица размерностью 24 x 96, элементы которой (в силу (7)) определяются значениями функций N р в узлах КЭ Ve , e = 1, ..., M .
Подставляя (12) в (11) и выполняя условие dWa (6a)/ 56a = 0, получаем матричное соотношение [Ka ]6a = Fa , где [Ka ] – матрица жесткости; Fa – вектор узловых сил ДвКЭ Va , которые определяем по MM формулам [Ka ] = £[Ae f [Ke ][Ae ], Fa = £[Ae f Pe . e=1 e=1
W s = 2( 6 b ) T [ K s ] 6 b - ( 6 b ) T p s , (13)
где [ Kbs ], P b s , δ b s – матрица жесткости, векторы узловых сил и перемещений суперэлемента Gbs , определяемые в декартовой системе координат Oxyz (рис. 3).
Используя функции (7), узловые перемещения суперэлемента Gbs выражаем через узловые перемещения крупной сетки Ha ДвКЭ Vb , т. е. для векторов δ b s , δ a построим связь вида
6 b = [ A s ] 6 a , (14)
где [ Abs ]– прямоугольная матрица, элементы которой (в силу (7)) определяются значениями функций N ^ в узлах суперэлемента Gbs .
Подставляя (14) в (13) и выполняя условие d Ws ( 6 a )/ д 6 a = 0, получаем матричное соотношение [ K b ] 6 a = F b , где [ Kb ] – матрица жесткости; F b – вектор узловых сил ДвКЭ Vb , которые определяем по формулам [ K b ] = [ A s ] T [ K b ][ A s ], F b = [ A s ] T P b .
Процедура определения напряжений в базовых КЭ ДвКЭ Vb аналогична п. 2.1.1. Как показывают расчеты, ДвКЭ Vb (построенные по 2-й процедуре) порождают более точные решения, чем ДвКЭ Va (построенные по 1-й процедуре). Однако 2-я процедура включает построение суперэлементов, что связано с обращением матриц высокого порядка. Это усложняет алгоритм и увеличивает временные затраты на реализацию 2-й процедуры на ЭВМ. Криволинейные ДвКЭ 1-го, 2-го порядка с неоднородной (микронеоднород-ной) структурой, строим по процедурам, аналогичным процедурам п. 2.
-
3. Композитные криволинейные сложные МнКЭ
Рассмотрим процедуру построения композитных криволинейных сложных МнКЭ (не теряя общности суждений) на примере сложного МнКЭ Vm 3-го порядка с характерными размерами hZ x hm x hZ, который имеет неоднородную структуру и расположен в локальной декартовой системе координат Oxyz (рис. 3). Область МнКЭ Vm представляем криволинейными ДвКЭ Vnb 3-го порядка, построенными по алгоритмам, аналогичным п. 2. Базовые дискретные модели ДвКЭ Vnb состоят из однородных криволинейных КЭ Ve 1-го порядка с характерными размерами he x hy x he (см. рис. 1) и учитывают неоднородную структуру ДвКЭ V„b, т. е. сложного МнКЭ Vam. Пусть he, he, a = const, где e = 1, ..., M„ , M„ - об-y z e "—a "—a щее число КЭ Ve базовой дискретной модели МнКЭ Vm . ДвКЭ Vnb с характерными размерами bZ x by x bZ расположен в локальной декартовой системе координат O1 x1 y1 z1, причем ось Oy МнКЭ Vm параллельна оси O1 y1 ДвКЭ vZ , где n = 1, ...,N, N - общее число ДвКЭ vZb. Для рис. 3 имеем N = 27, h™ = 3b^., hm = 3by - толщина, hm = 3bn - длина МнКЭ Vm . Пусть by,bZ,Yn = const, n = 1, ...,N.
На мелких сетках ДвКЭ Vnb определяем крупную сетку Hm МнКЭ V Z . Узлы сетки Hm равномерно расположены на ребрах МнКЭ V m , по 4 узла на каждом ребре (рис. 3), узлы отмечены точками (32 узла).
Отметим, что МнКЭ V α m включает конечное множество криволинейных различных мелких и крупных вложенных сеток ДвКЭ Vnb и крупную сетку Hm . При мелких разбиениях угол раствора α m МнКЭ V α m мал. Тогда формы МнКЭ V α m и прямоугольного параллелепипеда мало отличаются. В связи с этим при построении аппроксимирующих функций перемещений um , vm , wm для сложного МнКЭ V α m (рис. 3), определяемых по МКЭ на крупной сетке Hm , используем полиномы 3-го порядка [7; 8] и поэтому МнКЭ V α m называем сложным МнКЭ 3-го порядка. Функции um , vm , wm запишем в форме
32 32 32
u m = ∑ N i mu i m , v m = ∑ N i mv i m , w m = ∑ N i mw i m , (15) i = 1 i = 1 i = 1
где Nim – базисная функция i -го узла крупной сетки Hm ; uim , vim , wim – значения перемещений в i -м узле сетки Hm , определяемые в декартовой системе координат Oxyz , i = 1, ..., 32 .
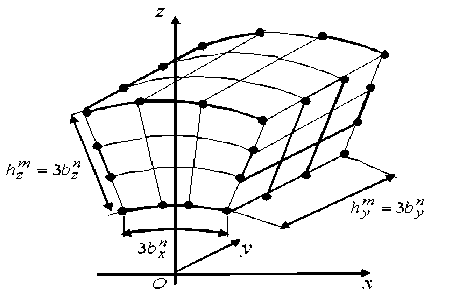
Рис. 3. Сложный МнКЭ V α m
Обозначим через qαm вектор узловых перемещений (размерностью 96) крупной сетки Hm в декартовой системе координат Oxyz , т. е. qαm есть вектор узловых перемещений сложного МнКЭ Vαm . Пусть ось O1y1 параллельна оси Oy и между осями O1x1 и Ox угол равен ϕn . Пусть векторы δ1n , δbn узловых перемещений ДвКЭ Vnb , отвечающие соответственно системам координат O1x1y1z1 и Oxyz , имеют структуру вида (4). Между векторами δ1n , δbn установим связь δ1n= [Tnb]δbn, где [Tnb] – матрица вращений, имеющая такую же структуру, как и матрица вращений [Te ] (см. формулу (9)). Учитывая, что δ1n= [Tnb]δbn, получим соотношения [Knb]= [Tnb]T× × [K1n][Tnb], Pnb=[Tnb]Pn1, где [Kn1], [Knb] – матрицы жесткости; Pn1 , Pnb – векторы узловых сил ДвКЭ Vnb , отвечающие соответственно декартовым системам координат O1x1y1z1 и Oxyz , n= 1, ..., N. Полную потенциальную энергию Wαm сложного МнКЭ Vαm представляем матричным выражением
N
W α m = ∑ (1( δ b n ) T [ K n b ] δ b n - ( δ b n ) T P n b ). (16)
n = 1 2
Используя функции (15), узловые перемещения b вектора δn выражаем через узловые перемещения крупной сетки Hm сложного МнКЭ Vαm , т. е. между векторами δbn , qαm установим связь вида
δ b n = [ A n m ] q α m , (17)
где [ Anm ] – квадратная матрица размерности, элементы которой (в силу (15)) определяются значениями функций Nim в узлах ДвКЭ Vnb , n = 1, ..., N .
Подставляя (17) в (16) и выполняя условие ∂Wαm(qαm)/∂qαm=0, получим матричное соотношение [Kαm]qαm=Fαm, где [Kαm], Fαm – матрица жесткости и вектор узловых сил сложного МнКЭ Vαm , которые N определяем по формулам [Kαm] = ∑[Anm]T[Knb][Anm], n=1
N
F α m = ∑ [ Anm ] T P n b . Криволинейные сложные МнКЭ n = 1
1-го и 2-го порядка с неоднородной (микронеодно-родной) структурой, которые геометрически подобны форме сложного МнКЭ V α m , строим по процедуре, аналогичной процедуре п. 3.
3.1. Процедура определения напряжений в сложном МнКЭ Vαm. Пусть найден вектор qαm узловых перемещений МнКЭ Vαm , отвечающий системе координат Oxyz (рис. 3). По формуле (17) находим вектор δbn узловых перемещений ДвКЭ Vnb , n= 1, ..., N. С помощью матрицы вращений [Tnb ] вектор δ1n узловых перемещений ДвКЭ Vnb определяем (в системе координат O1x1y1z1 ) по формуле δ1n= [Tnb]δbn. Используя вектор δ 1n , напряжения в КЭ Ve базового разбиения ДвКЭ Vnb вычисляем по процедуре, аналогичной процедуре п. 2.1.1.
4. Результаты расчетов
В качестве модельной задачи рассмотрим расчет в безразмерных параметрах цилиндрической трехслойной оболочки V0 постоянной толщины h , которая расположена в декартовой системе координат Ox0y0z0(рис. 4). При y0 = 0 имеем u=v=w=0 , т. е. левый торец оболочки жестко закреплен. Жесткие (верхний и нижний) слои составляют 1/6 толщины оболочки и параллельны оси Oy0 . Модуль Юнга связующего материала равен 1, жестких слоев – 10, коэффициент Пуассона для жестких слоев и связующего материала равен 0,3. Радиус внутренней поверхности оболочки равен 140, радиус внешней поверхности - 150, толщина оболочки h = 10, длина L = 350 . На верхней поверхности S0 оболочки, симметричной относительно плоскости Oy0z0, приложена равномерно распределенная радиальная нагрузка q = 0,01. Область S0 на рис. 4 заштрихована, угол раствора а области S0 равен п /2 . В расчетах, силу симметричного вида нагружения, используем половину оболочки относительно плоскости Oy0z0. Базовая дискретная модель R0 оболочки V0 состоит из однородных криволинейных КЭ Ve 1-го порядка с характерными размерами he х hy х he (см. рис. 1). Базовая модель R0 оболочки V0 учитывает ее неоднородную структуру и порождает мелкую сетку h0 размерностью 145 х109 х 7, h = 6 he . Имеем hy, he, а e = const, где e = 1, ..., M ; M - общее число КЭ Ve.
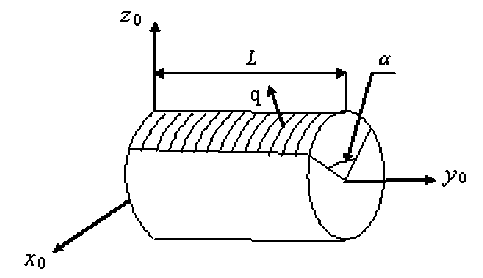
Рис. 4. Схема нагружения оболочки
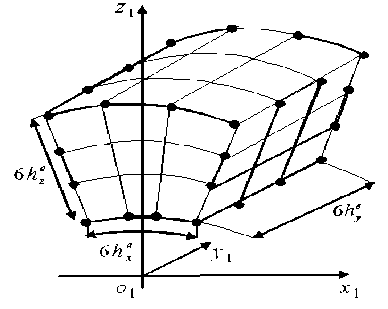
Рис. 5. ДвКЭ Vnd
Многосеточная дискретная модель Rh оболочки V0 состоит из криволинейных сложных МнКЭ Vm 3-го порядка с характерными размерами 18he х18hy х 6he, мелкие сетки которых имеют размерность 19 х 19 х 7 . Сложные МнКЭ Vm построены по процедуре, анало гичной процедуре п. 3, а = 1, ..., N0, N0 - общее число МнКЭ Vm , N0 = 48.
При построении сложных МнКЭ V m используем девять криволинейных ДвКЭ Vnd 3-го порядка с характерными размерами 6 h e х 6 h y х 6 h e (рис. 5), которые построены по процедуре п. 2.2 и мелкие сетки которых имеют размерность 7 х 7 х 7 . Результаты расчетов оболочки V 0 показывают, что максимальное эквивалентное напряжение □ m = 2,206 (вертикальное перемещение wm = 156,188) многосеточной модели R m отличается от максимального эквивалентного напряжения а 0 = 2,270 (перемещения w 0 = 158,153) базовой модели R 0 оболочки на 2,81 % (на 1,24 %). Размерность базовой модели R 0 равна 327348, ширина ленты системы линейных алгебраических уравнений (СЛАУ) МКЭ – 2295. Многосеточная модель R m оболочки V 0 имеет 1776 узловых неизвестных, ширина ленты СЛАУ МКЭ равна 252. Реализация МКЭ для многосеточной модели R m требует в 1678 раз меньше объема памяти ЭВМ, чем для базовой модели R 0 . Построение решения для многосеточной дискретной модели R m требует в 420 раз меньше временных затрат, чем для базовой модели R 0 . Эквивалентные напряжения определяем по 4-й теории прочности в центрах тяжести КЭ Ve базовой модели R 0 оболочки.
Заключение. В данной работе показаны процедуры построения композитных криволинейных сложных МнКЭ 1-го, 2-го и 3-го порядка. Достоинства предлагаемых конечных элементов состоят в том, что они:
-
- описывают трехмерное напряженное деформированное состояние в композитных цилиндрических оболочках;
-
- учитывают неоднородную (микронеоднород-ную) структуру оболочек;
-
- порождают многосеточные дискретные модели оболочек, размерности которых на несколько порядков меньше размерностей базовых дискретных моделей;
-
- учитывают сложный характер крепления и нагружения оболочек.
Реализация МКЭ для многосеточных дискретных моделей композитных цилиндрических оболочек требует мало временных затрат и значительно меньше объема памяти ЭВМ, чем для базовых моделей.
Acknowledgments. This work was financially supported by RFBR (code project 14-01-00130).
Список литературы Расчет композитных цилиндрических оболочек с применением многосеточных элементов
- Болотин В. В., Новиков Ю. Н. Механика многослойных конструкций. М.: Машиностроение, 1980. 375 с.
- Голушко С. К., Немировский Ю. В. Прямые и обратные задачи механики упругих композитных пластин и оболочек вращения. М.: ФИЗМАТЛИТ, 2008. 432 с.
- Андреев А. Н., Немировский Ю. В. Многослойные анизотропные оболочки и пластины: изгиб, устойчивость, колебания. Новосибирск: Наука, 2001. 288 с.
- Киселев А. П. Расчет тонких оболочек на прочность в трехмерной постановке без упрощающих гипотез//Изв. вузов. Сер. «Строительство». 2008. № 1. С. 18-23.
- Москвичев В. В. Основы конструкционной прочности технических систем и инженерных сооружений. Ч. 1. Постановка задач и анализ предельных состояний. Новосибирск: Наука, 2002. 106 c.
- Сегерлинд Л. Применение метода конечных элементов в технике. М.: Мир, 1975. 541 с.
- Зенкевич О. Метод конечных элементов в технике. М.: Мир, 1975. 541 с.
- Норри Д., де Фриз Ж. Введение в метод конечных элементов. М.: Мир, 1981. 304 с.
- Матвеев А. Д. Некоторые подходы проектирования упругих многосеточных конечных элементов/Ин-т вычислительного моделирования СО РАН. Красноярск, 2000. 30 с. Деп. в ВИНИТИ № 2990-В00.
- Матвеев А. Д. Многосеточное моделирование композитов нерегулярной структуры с малым коэффициентом наполнения//ПМТФ. 2004. № 3. С. 161-171.
- Матвеев А. Д. Построение сложных многосеточных элементов с неоднородной и микронеоднородной структурой//Известия АлтГУ. Сер. «Математика и механика». 2014. № 1/1. С. 80-83.
- Самуль В. И. Основы теории упругости и пластичности. М.: Высш. шк., 1982. 264 с.
- Матвеев А. Д., Гришанов А. Н. Смешанные многосеточные дискретные модели трехмерных цилиндрических композитных панелей и оболочек сложной формы//Сб. ст. XIX зимней школы по механике сплошных сред. Пермь, 2015. С. 198-211.
- Матвеев А. Д., Гришанов А. Н. Многосеточные криволинейные элементы в трехмерном анализе цилиндрических композитных панелей с полостями и отверстиями//Ученые записки Казанского университета. Сер. «Физико-математические науки». 2014. Т. 156, кн. 4. С. 47-59.
- Матвеев А. Д., Гришанов А. Н. Расчет композитных цилиндрических панелей и оболочек с учетом их структуры на основе свыше миллиарда уравнений МКЭ с малыми временными затратами//Численные методы решения задач теории упругости и пластичности: материалы ХХIV Всерос. конф. Омск: Изд-во ОмГТУ, 2015. С. 141-150.


