Расчет контактных напряжений при совмещенной прокатке-прессовании

В теории совмещенной прокатки-прессования (СПП), как и в теории других процессов ОМД, важное практическое значение имеет определение контактных напряжений. От величины и характера распределения контактных напряжений по длине очага деформации зависят энергосиловые параметры процесса СПП, которые служат основными критериями при разработке технологии и проектировании оборудования для процесса СПП.

В настоящее время одним из наиболее распространенных методов определения контактных напряжений является совместное решение уравнений равновесия и пластичности, в частности решение дифференциального уравнения прокатки с определенными граничными условиями и упрощающими допущениями.

Впервые математический анализ контактных напряжений при прокатке проведен Т. Карманом [1], а затем А.И.Целиковым [2], который рассмотрел более общий случай, когда прокатываемая полоса при входе в валки и выходе из них подвергается натяжению, и получил следующее уравнение:

τ dh dPx = (^s ±  ---)    ,                               (1)

tgϕX hX где знак плюс – для зоны опережения, а знак минус – для зоны отставания; βL = 1,15 – коэффициент вида напряженного состояния Лоде; σ S – сопротивление металла деформации; τ – напряжение трения; h и ϕ – текущая высота и центральный угол очага деформации.

XX

Конкретные решения уравнения (1) могут быть разными в зависимости от выбора закона трения, изменения геометрических характеристик очага деформации ф X , h_X и других условий.

Методика расчета давления и силы прокатки в прямоугольных (ящичных) калибрах разработана В. М. Клименко [3]. В работах В.Н. Выдрина и Л.М. Агеева [4], В.М. Салганика и А.М. Песина [5] представлены методики, расчетные алгоритмы и результаты численного исследования на ЭВМ контактных напряжений при асимметричной прокатке. Однако формулы для определения энергосиловых параметров, полученные для условий прокатки в гладких и сортовых валках, не применимы для процесса СПП.

Теоретические исследования контактных напряжений для процесса СПП в работах Н.Н. Довженко и С.Б. Сидельникова [6], В.Н. Корнилова [7] были получены на основе математической модели симметричного очага деформации, что требует проведения дополнительного анализа и создания новой методики для их определения.

Методика расчета контактных напряжений для процесса совмещенной прокатки-прессования

При выводе дифференциального уравнения для процесса СПП примем, что изменение сил трения подчиняется закону Зибеля, а остальные допущения будут такие же, что и у А.И. Целикова [2]:

т = ^s ,                                     (2)

где μ – коэффициент трения.

При определении контактных напряжений используем совместное решение уравнений равновесия и пластичности для каждой характерной зоны асимметричного очага деформации при СПП.

Вначале рассмотрим равновесие элемента высотой h + dx и толщиной dx, выделенного в x очаге деформации зоны прокатки (рис. 1). Его положение определяется углом ф или координатой x. При этом начало координат поместим в точке О, а ось x направим в противоположном направлении движению металла.

Найдем сумму горизонтальных проекций всех сил, действующих на выделенный элемент:

n

Е F ix = ^Ш + d ^ x X h x + dh x ) b + CT x ^ x b + ² P x bR nP sin Ф ^d Ф + ^T 1 ^bRnP^d Ф + i = 1

+(t2 bRПpdф + 2т hRnPd?) = 0,(3)

. _  __ где знак плюс - для зоны опережения, а знак минус - для зоны отставания; т1,т 2 ,тK - напряжения трения на верхнем и нижнем валках и на боковых стенках калибра соответственно;

_ 2 R 1 R ₂

RΠP =       – приведенный радиус прокатки.(4)

R1 + R 2

Сократив все слагаемые уравнения (3) на ширину калибра b, раскрыв скобки и пренебрегая бесконечно малыми величинами второго порядка, получим:

-^ x dh x - h x d o x + 2 p_xR_n P sin dPф + T 1 R_npdp^ v ( t ₂ R _n P d( p + 2 T K h 1 R_npd p Ib ) = 0.        (5)

Учтем, что h_x = h 1 + R_nP d ²; dh x = 2 R_ПP d d ф ; d ^ x = dp x ; sin Ф = Ф ; P_x — ^ = e L G' S ;

T i e* 1 S ; т 2     ^ 2 ^ S "

Подставив данные выражения в ( 5), окончательно получим дифференциальное уравнение для процесса СПП, где в качестве переменной принимается текущий угол ф - :

dp_x = ^ ^sRnp 2 [2 в^ + а Т А (1 + ^m K h^A d d ,                    (6)

прФ здесь mK = тK /т2 - коэффициент отношения напряжений трения, действующих по боковым стенкам тK и по дну т2 калибра; ц1, ц2 - коэффициенты трения на валках.

Для упрощения решения примем, что толщина полосы на протяжении очага деформации

_ , h + 2 h _ остается постоянной и равной hCP =------. Тогда после интегрирования (6) получим:

^a S _a R_nP     2 _    _ _п 2 m_Kh 1

Px =  7---[вLф + R№ + ^2ф( + 7 )] + Ca , hCP где Са - постоянная интегрирования находится из условия, что на входе в зону прокатки p (а) = вЛ^5я (с$а - сопротивление деформации в области прокатки):

R„„ х              2 mA .

Ca = ^SakPL - -7— [eLa +А1а W(1 +  , )]L hCP

^{С помощью} уравнен™ ^{(7) и (8) можно определить} контактные ^{напряжения в зоне прокат}ки при 0 <  ф <  а . Расчет проводится в последовательности от входа в зону прокатки и до оси прокатки с учетом значений нейтральных углов на валках и расположения характерных зон в зоне прокатки. Постоянные интегрирования в каждой характерной зоне должны обеспечивать равенство контактных напряжений на границах соседних зон.

При расчете контактных напряжений в зоне прессования так же, как и для зоны прокатки, рассмотрим равновесие элемента высотой h + dh и толщиной dx , выделенного в очаге деформации зоны прокатки (рис. 2). Его положение определяется углом ф _x или координатой x . Начало координат поместим в точке О , а ось х направим по направлению движения металла.

В соответствии с принятой методикой проведем аналогичные математические выкладки для зоны прессования и найдем уравнения для расчета контактных напряжений:

Рх = CTS®Rnp [-eLd2 ± М1Ф ± ИМ1 + ^mKh1-^ + C6, hCP где Cθ – постоянная интегрирования находится из условия, что на выходе из зоны распрессовки px (5) = стПР + eL^Se (а4в - сопротивление деформации в области прессования):

Ce = а пр + as, в - -ПР [-eL^2 ± R19 ± Ц1^\ + —р)]}.(10)

hCP

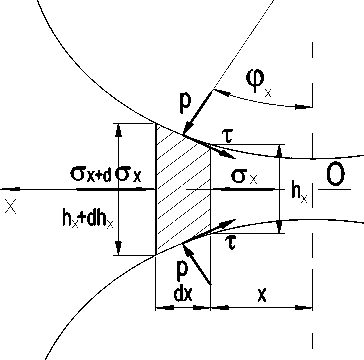
Рис. 1. Схема к расчету контактных напряжений в зоне прокатки

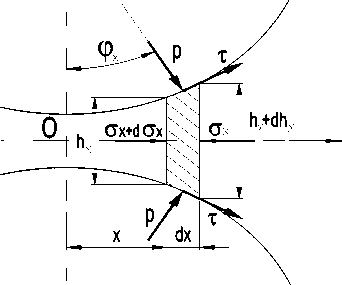
Рис. 2. Схема к расчету контактных напряжений в зоне прессования

С помощью уравнений (9) и (10) можно определить контактные напряжения в зоне прессования при 0 < ф < 0 .

Применим разработанную методику определения контактных напряжений для анализа динамики процессов СПП с одним и двумя приводными валками. В качестве примера рассчитаем эпюры контактных давлений для конкретных условий процесса СПП: заготовка из алюминиевого сплава АД31 размерами h ₀ • b ₀ = 14 - 14 мм, которая при температуре 480 ⁰С во время прокатки получала обжатие е h = 55 % ( h 1 = 6,3 мм) и выдавливалась в пруток диаметром d_np = 7,0 мм (X пр = 6,7). Матрица имела высоту h_M = 20 мм ( 0/а = 1,33 ). Валки радиусами R 1 = 107 мм и R ₂ = 81,25 мм вращались с одинаковой скоростью п вр = 4,0 об/мин ( ю 1 = ш , = 0,42 с^-1). В случае СПП с одним приводным валком - валок радиусом R 1 = 107 мм был неприводным.

По методике, представленной в работе автора [8], определяем нейтральные углы для обоих видов СПП:

• -    с двумя приводными валками: у 1 = 0,5 0 и у ₂ = 8,5 0 ;

• -    с одним приводным валком: у 1 = 11,8 0 и у ₂ = 2,0 0 .

  

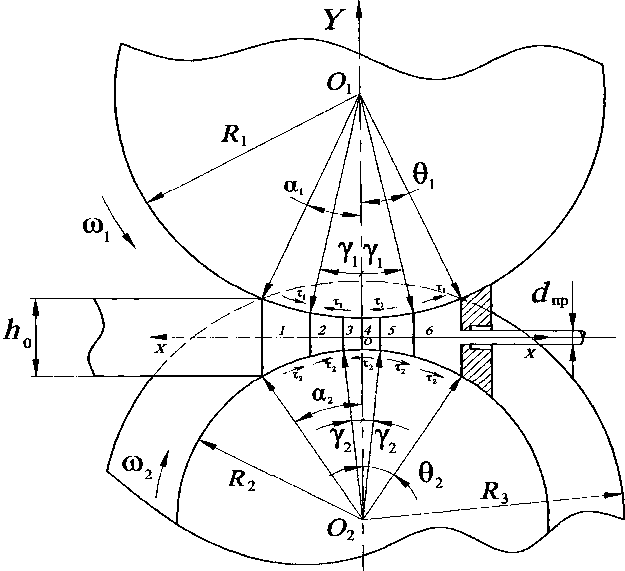
  Рис. 3. Характерные зоны очага деформации при СПП: 1 – зона отставания прокатки; 2 – переходная зона прокатки; 3 – зона опережения прокатки; 4 – зона опережения прессования; 5 – переходная зона прессования; 6 – зона отставания прессования

  
  

Далее приводим найденные углы к одной угловой координате с помощью приведенного радиуса прокатки R_ПР :

^γ ПPi

R i γ i R_ПР

Сопоставляя приведенные нейтральные углы на валках, определяем размеры характерных зон. В случае процесса СПП с двумя приводными валками Y _{nP 2} >  Y _nP 1 , поэтому в области прокатки будут следующие зоны вдоль оси прокатки (рис. 3).

В случае процесса СПП с одним приводным валком соотношение нейтральных углов другое - Y _nP 1 >  Y _{nP 2}, поэтому размеры характерных зон будут тоже другими.

Для каждой характерной зоны уточняем дифференциальное уравнение равновесия, интегрируем его и находим произвольную постоянную из граничных условий.

Для СПП с двумя приводными валками получим уравнения для определения контактных давлений.

• -    В области прокатки:

для зоны отставания при а_№ > ф> y _№ 2 :

Рх 1 (Ф) = в^а + CTSaRnP [в (Ф2 — а 2) — ^1 (Ф — а) — Мг(Ф - а )(1 + 2^;^L)], hCP> 1                                                              b для переходной зоны при Ynp2 > Ф > Ynp 1 :

CSaRnP,R ^^Hm mKhA^.p pX 2(Ф) = —-----VвLФ +---------) + C 2,(13)

hCP 2

где C ₂ = p_X , ( y ₂) - p X ₂ ( y ₂) - произвольная постоянная;

для зоны опережения при Y np 1 >  Ф >  0 :

, . ^ Rhpvr        _л 2 тД.-

Рхз№ = Sa ПР W + № + ^1 +  K)] + C3, hCP з где C3 = pX2 (Yj ) - pX3 (Yi) — произвольная постоянная.

• -    В области прессования:

для зоны опережения при 0 < ф <  Y np 1 :

, X ^еRnpv о 2           „ 2 m_Kh

Рх4 (Ф) = S8 ПР [-РъФ + WP + ^(1 + hCP 4

где C . = p , , (0) ^{- p} _{v 4}(0) = С , , - произвольная постоянная;

для переходной зоны при Y _nP 1 ^ Ф- Y _{nP 2}:

Рх ,(,) = ^S^RnP- (-в,- + 2-^) + C5, hCP 5

где C 5 = Р х 4 ⁽ Y 1 ) ^- Р х 5 ⁽ Y 1 ) ^- произвольная постоянная; 5 X 41 X 51

для зоны отставания при Y_{np 2} < ф < в :

Рх 6 (ф) = СТ пресс + eLOs6 - CSeRnP [eL (в2 - Ф2 ) + ^ (в - ^) + ^2 (в - ^)(1 + ^mKhL)].

hcp 6

где β – центральный угол расположения ОЧПЗ.

Для СПП с одним приводным валком уравнения для определения контактных давлений будут аналогичного вида, что и для СПП с двумя приводными валками.

Результаты теоретических исследований

Для иллюстрации результатов расчета на рис. 4 приведены теоретические эпюры распределения давления на границе контакта очага деформации при СПП.

Полученные зависимости отличны от результатов исследований других авторов [6; 7], которые не учитывали асимметрию и влияние переходных зон при СПП.

Получив уравнения распределения давлений по дугам контакта, можно определить среднее контактное давление, усилие и крутящий момент на валках, мощность процесса СПП по известным формулам в теории прокатки [9].

Среднее контактное давление можно выразить в виде интегральной суммы распределенных давлений:

Рср = ^-[“1р ( Ф )d ф + 1 Р p( Ф )4 ФА « -1- ]Г (Pi^ p^ ,         (18)

^а пр ⁺ Пп_Р 0              0               la ^{+ l}e i = 1        ²

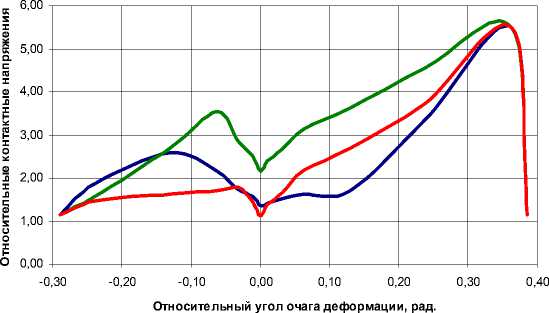
^^^^^* р/σs w ^^^^^^^ p/σs w ϲp ^^^^^^^ p/σs н/п

Рис. 4. Эпюры распределения относительного контактного давления вдоль очага деформации при СПП с двумя приводными валками c учетом p /σ S w и без учета асимметрии p / σ S wcp ; с одним приводным валком p /σ S н/п

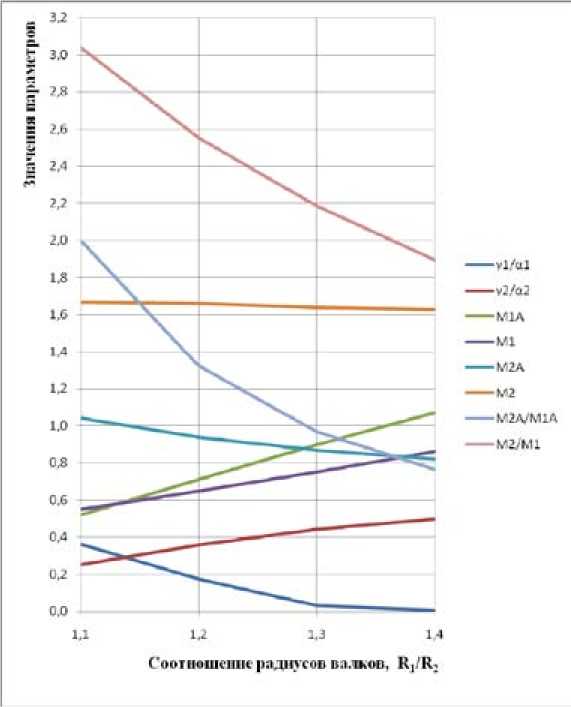
Рис. 5. Изменение крутящих моментов на валках М (в кН·м) с выступом (индекс «1») и с ручьем (индекс «2») с учетом асимметрии (индекс «А») и без нее, а также соотношений моментов M ₂ / M ₁ и нейтральных углов γ / α на валках от соотношения радиусов валков R ₂ / R ₁

Таблица 1. Энергосиловые параметры процесса СПП

Параметр процесса СПП Вид процесса СПП с двумя приводными валками без учета асимметрии с двумя приводными валками с одним приводным валком Среднее контактное давление, МПа 69,49 54,36 52,92 Усилие на валках, кН 60,55 47,37 46,11 где la, l0 - длина зоны прокатки и прессования соответственно; pi, p+1 - давление на входе и выходе из характерной i-й зоны очага деформации; li – длина характерной i-й зоны очага деформации.

Усилие на валках можно найти как произведение среднего контактного давления p_CP на площадь контакта деформируемого металла с инструментом F_K :

P b = P cp F k ” P cp b ( l a + l ₆ ).                                 (19)

Полный крутящий момент для одного валка с учетом различного направления сил трения в зонах отставания и опережения составляет:

• -    для валка с выступом

α _i γ _i γ _i θ _i δ _i

MCnni = bR( J TadP -J TadP - J Ted9 + J Ted9 -J TM dP)(20)

Yi               0               0              Yi0

• -    для валка с ручьем

_h α i γ i γ i θ i δ i

MCPnni = [ b + 2 hi(1 + 2R-)] R,( J Tadtp -J Tadtp -J Tedcp + J Tedcp -J Tm dp), где условные обозначения приняты такими же, как и в предыдущих разделах.

Допуская, что напряжения трения остаются постоянными на протяжении очага деформации, после интегрирования получим формулу крутящего момента, аналогичную той, которая впервые была предложена В.Ф. Баюковым [9]:

• -    для валка с выступом

M Спп. = bR- T a [ a . + К Д- Y (1 + K _T )],                         (22)

• -    для валка с ручьем

M Спп, = [ b + 2 h i (1 + ^^)] R,²T a [ a + К _т9, -y, (1 + K „ )],                   (23)

• ² R i

где K _a = ст _{$ в}/ст _{$ a} ; n S _a и □ S ₀ - сопротивление металла деформации в областях прокатки и прессования.

Полученные формулы (22) – (23) просты и вполне приемлемы для анализа и практических расчетов, но требуют обязательного определения нейтральных углов на валках.

Результаты расчетов энергосиловых параметров, проведенные с помощью полученных формул, представлены на рис. 5 и в табл. 1. В качестве примера рассмотрен процесс СПП с указанными параметрами. При этом радиус валка с ручьем принимался постоянным и равным R2 = 81,25 мм, а радиус валка с выступом R1 изменяли в соответствии диапазоном соотношений R 2 / R1 = 1,1 ^1,4 .

Выводы

Анализируя полученные результаты, можно отметить следующее:

• 1.    Во всех случаях СПП в зоне прокатки контактные напряжения имеют локальные максимальные значения в районе приведенных нейтральных углов Y_{nP 2} на валке с вырезом (ручьем), а в зоне прессования контактные напряжения увеличиваются, достигая своего абсолютного максимума в начале области выдавливания, что соответствует центральному углу в расположения ОЧПЗ.

• 2.    Максимальное значение контактных напряжений зависит в основном от вытяжки при выдавливании профиля.

• 3.    С увеличением отношения радиусов валков соотношения моментов на валках уменьшаются.

• 4.    Определение энергосиловых параметров без учета асимметрии процесса СПП [6; 7] завышает результаты расчетов.