Расчет квантовых характеристик на основе классического решения задачи дифракции в резонаторе с диэлектрической пластиной

Актуальность создания квантовой теории дифракционных оптических элементов основывается на том, что в настоящее время квантовые телекоммуникации приобретают первостепенное значение [1]. Квантовые телекоммуникации – это совокупность методов для передачи информации, закодированной в квантовых состояниях из одной точки в другую. Квантовая связь даёт возможность передавать информацию в зашифрованном виде [2–4].

Если квантов в импульсе 1000, есть вероятность, что 100 квантов по пути будет отведено злоумышленником на свой приёмник. В последующем, анализируя открытые переговоры между передающей и принимающей стороной, он может получить нужную ему информацию.

Поэтому в идеале число квантов в импульсе должно быть равно одному. В этом случае любая попытка отвода части квантов злоумышленником приведёт к существенному изменению всей системы в целом и, как следствие, росту числа ошибок у принимающей стороны. В подобной ситуации принятые данные должны быть отброшены, а попытка передачи повторена.

Сигналы передаются с помощью потока одиночных фотонов. Фотон невозможно разделить, измерить, скопировать или незаметно убрать [5–8]. Из-за подобных действий фотон просто разрушается и не может дойти до своего получателя [9– 12]. Это делает невозможным несанкционированный перехват сообщений третьими лицами.

На рис. 1 представлена оптическая схема установки, используемой в современной квантовой криптографии. Передающая сторона находится слева, а принимающая – справа. Ячейки Поккельса необходимы для импульсной вариации поляризации потока квантов передатчиком и для анализа импульсов поляризации приёмником. Передатчик может формировать одно из четырёх состояний поляризации. Передаваемые данные поступают в виде управляющих сигналов на эти ячейки. В качестве канала передачи данных может быть использовано оптоволокно. В качестве первичного источника света можно использовать и лазер. На принимающей стороне после ячейки Поккельса установлена кальцитовая призма, которая расщепляет пучок на два фотодетектора (ФЭУ), измеряющих две ортогональные составляющие поляризации. Представляет интерес, как одиночные фотоны проходят через обычные оптические элементы.

Другой пример, где проявляется квантовая природа света, – это оптические системы формирования изображения с малым числом фотонов. Примером могут служить системы дистанционного зондирования Земли, особенно космические изображающие гиперспектрометры, в которых ослабленный поступлением через узкую щель входящий световой поток ещё и распределяется по длинам волн [13– 15]. Даже на освещённой стороне Земли количество света недостаточно. Это приво- дит к тому, что в этих системах используются зеркала огромных размеров (конечно, зеркало с большой апертурой необходимо не только для того, чтобы интенсивность изображения была достаточна для регистрации датчиками, но и для повышения разрешения). В качестве главного собирающего оптического элемента такого телескопа можно использовать очень тонкую и лёгкую мембрану диаметром 20–30 метров [16]. Дифракционный муаровый узор мембраны сфокусирует свет на объективе камеры. Сам спутник предполагается запустить на геостационарную орбиту (36 тысяч километров). На этой орбите Земля является неподвижной. Это позволит исключить эффекты, связанные с явлением смаза на изображении. Только в этом случае камеры спутника могут уловить на поверхности Земли что-то полезное для различных применений. Изучая взаимодействие пучков с малым числом фотонов с датчиками, можно построить оптические системы с высоким разрешением. На основе строгой теории возможно построение приборов, которые фиксируют не только интенсивность, но и корреляции фотонов. Возможно также создание квантовых изображающих гиперспектрометров, которые используют информацию о корреляции фотонов в различных точках изображения.

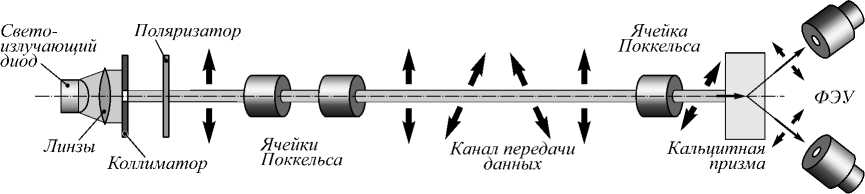
Рис. 1. Оптическая схема установки, используемой в современной квантовой криптографии

В данной работе описана процедура квантования электромагнитного поля в резонаторе с идеально отражающими стенками при наличии диэлектрической пластины. С этой целью получены выражения для собственных мод резонатора с диэлектрической пластиной. Также получены выражения для операторов векторного магнитного потенциала и напряжённости электрического поля. Кроме того, получены выражения для (среднего) наблюдаемого значения распределения напряжённости электрического поля и квадрата напряжённости электрического поля в многофотонном состоянии.

1. Моды 1D-резонатора с диэлектрической пластиной

где Ф m ( x ) удовлетворяет уравнению Гельмгольца:

ф;( x ) + k m n ² ( x ) Ф m ( x ) = 0,                      (3)

k m = to _m / c и c - скорость света.

Слева от диэлектрика

Ф 1 ( x ) = P 1 sin ( k ( x + 1 1 ) ) .                               (4)

Внутри диэлектрика с показателем преломления n :

Ф ²( x ) = P ₂sin ( knx ) + R ₂cos ( knx ) .                 (5)

Справа от диэлектрика

В случае когерентного состояния выражение для среднего значения представляет собой просто выражение для разложения векторного потенциала по модам резонатора. Рассмотрим область – l 1 <  x <  l 2 . При x =0 находится граница раздела диэлектрика (см. рис. 2).

Ф ³( x ) = T jsin ( k ( x - 1 ₂ ) ) .                              (6)

Соответствующие производные имеют вид

Диэлектрическая Зеркало пластина / /

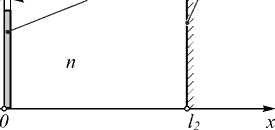
Рис. 2. Схема 1D-резонатора с диэлектрической пластиной

дФ 1 ( x )

—д---= P1 k cos (k (x +11)), дФ2( x)

—д--- = P ₂ kn cos ( knx ) - R ₂ kn sin ( knx ) ,          (7)

дФ ³( x )

—д--- = P ₃ k cos ( k ( x - 1 ₂ ) ) .

Условие сшивки при x =0:

Решение волнового уравнения для потенциала

P sin ( k1 1 ) = R ₂, P cos ( k1 1 ) = P ₂ n .

д2 A (x, t) n2 (x )д2 A (x, t)

д x ²        C²     d t² "

После деления одного уравнения в (8) на другое получаем:

имеет вид

A ( x ’ t ) = Z ° m ( x ) [ F m cos ( ® m t ) + G m sin ( ® m t ) ] , (2) m

n sin ( k1 1 ) R ₂ cos ( k1 1 ) P ₂

Условие сшивки при x = d :

P₂ sin ( knd ) + R 2 cos ( knd ) = P₃ sin ( k ( d - 1 2 ) ) , P₂n cos ( knd ) - R 2 n sin ( knd ) = P₃ cos ( k ( d - 1 2 ) ) .

Аналогично после деления одного уравнения в (10) на другое получаем:

P ₂sin ( knd ) + R ₂cos ( knd ) sin ( k ( d - 1 2 ) ) P₂ n cos ( knd ) - R ₂ n sin ( knd ) cos ( k ( d - 1 ₂ ) )

Преобразовываем (11) к виду

Г             R,         .x)

sin( knd ) + —cos( knd ) cos( k(d - 1 ₂)) =

I            P 2           -

Г         R

= n cos( knd )—² n sin( knd ) sin( k(d - 1 ₂)).

I              P2           ^J

P ₂ = P l cos ( k1 1 ) [n , P₃ = P l cos ( k1 1 ) [C ,

R ₂ = P l sin ( k1 1 ) ,

где

C = n sin ( knd ) sin ( k ( d - 1 ₂ ) ) + + cos ( knd ) cos ( k ( d - 1 ₂ ) ) .

Решая дисперсионное уравнение (13) относительно k , находим множество его решений k m . Поиск решений k m осуществляется в некотором заданном диапазоне k e [ k mi _n, k max ]. В результате получаем, что моды резонатора с диэлектрической пластинкой имеют следующий вид:

Подставляя (9) в (12), получаем дисперсионное уравнение:

Ф m ( x ) =

Ф 1 т ( X ) = P m ■ sin

- 1 i <  x <  0,

[ sin ( knd ) cos ( k1 1 ) + n sin ( k1 1 ) cos ( knd ) ] x

x cos (k (d -12)) =

= |^ n cos ( knd ) cos ( k1 1 ) - n ² sin ( k1 1 ) sin ( knd ) ]x x sin ( k ( d - 1 ₂ ) ) .

Решением дисперсионного уравнения (13) является набор волновых чисел k m . Далее для каждого найденного k m , используя систему уравнений (8) и (10):

P sin ( k1 i ) = R 2 ,

P cos ( k1 i ) = P 2 n ,

< P ₂sin ( knd ) + R ₂cos ( knd ) = P 3 sin ( k ( d - 1 ₂ ) ) ,   (14)

P ₂ n cos ( knd ) - R ₂ n sin ( knd ) =

= P3 cos (k (d -12)), нужно найти неизвестные коэффициенты P1, P2, R2, P3.

Так как три коэффициента можно выразить через первый, то выбросим в (14) второе уравнение, тогда:

R 2 = P l sin ( k1 i ) ,

< P 2 sin ( knd ) + R ₂cos ( knd ) - P₃ sin ( k ( d - 1 ₂ ) ) = 0,   (15)

P₂n cos ( knd ) - R ₂ n sin ( knd ) - P₃ cos ( k ( d - 1 ₂ ) ) = 0.

Ф ²т ( X ) = P m

cos ( k m 1 i )

---------sin ( k m nx ) + n

= <

+sin (km11) cos (kmnx)], 0 < x < d, sin I km (x - 12 )l

Ф т ( x ) = P m cos ( k m 1 i )---------- , d <  x <  1 2 ,

Cm где

C m = n sin ( k m nd ) sin ( k_m ( d - 1 ₂ ) ) +

+ cos(kmnd)cos(km (d -12)), а Pm – вычисляется из условия нормировки базисных функций:

l ₂

j n ² ( x ) Ф m ( x ) Ф т ( x ) d x = 1.                      (20)

• - 1 1

В частном случае, когда резонатор пустой, дисперсионное уравнение (20) принимает следующий вид:

sin ( k1 1 ) cos ( k1 ₂ ) + cos ( k1 1 ) sin ( k1 ₂ ) = 0.             (21)

Корни уравнения (21) можно вычислить аналитически:

Учитывая первое уравнение, перепишем систему (15):

P ₂ sin ( knd ) + P 1 sin ( k1 1 ) cos ( knd ) -

• - P₃ sin ( k ( d - 1 ₂ ) ) = 0,

P ₂ n cos ( knd ) - P l sin ( k1 1 ) n sin ( knd ) -

• - P 3 cos ( k ( d - 1 2 ) ) = 0.

_ n m

= ( 1 1 + 1 2 ) .

Также моды пустого резонатора имеют простой аналитический вид:

Ф m ( x ) =

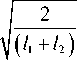
sin

n m

x( 11 + 12 )

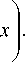
После преобразований решаем систему (16) и получаем:

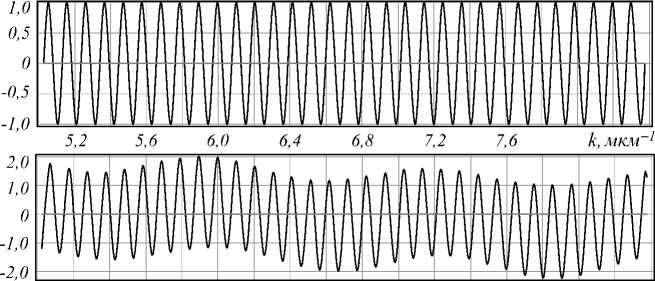
Рассмотрим в качестве примера резонатор при следующих параметрах расчёта: длина резонатора l2 = l1 =30 мкм, диэлектрическая пластинка толщиной d =2 мкм с показателем преломления n = 1,5, kmm = 5 мкм-1, kmax = 8,4 мкм-1. На рис. 3 показаны результаты расчёта km (соответствуют координатам пересечения графика для уравнения (20) нулевой линии) для пустого резонатора (рис. 3а) и резонатора с диэлектрической пластинкой (рис. 3б). Как видно, при наличии диэлектрической пластинки набор km, соответствующий решениям дисперсионного уравнения (20), не имеет линейной зависимости.

На рис. 4 показаны примеры мод резонатора с диэлектрической пластинкой толщиной d =2 мкм и показателем преломления n = 1,5. Хорошо видно, что с увеличением индекса моды частота её растёт. Также видно, что в области пластинки (0< x <  d ) происходит «сбой» гармонического характера моды.

б)

5,2      5,6       6,0       6,4       6,8       7,2       7,6

к, МКМ *

Рис. 3. Результаты расчёта k m для пустого резонатора (а) и резонатора с диэлектрической пластинкой (б)

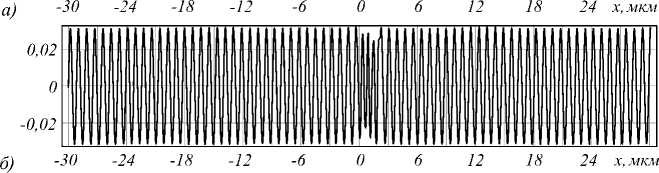
Рис. 4. Графики мод резонатора с диэлектрической пластинкой толщиной d=2 мкм и показателем преломления n=1,5: m=14 (а), m=47 (б)

2. Прохождение импульса в резонаторе

Использование коротких импульсов в системах телекоммуникаций становится всё актуальнее. При этом наблюдаются различные пространственновременные эффекты [17–20], особенно для ультракоротких импульсов [21 – 24].

Выражение для потенциала (2) можно записать в виде:

A ( x , t ) = ^ Ф m ( x ) { b m exp ( - i ® m t ) + b m exp ( i ® m t ) } , (24)

где b m =( F m + iG m )/2.

Коэффициенты поля (2) вычисляются на основе начального распределения потенциала:

b

Fm = j A(x,0)Фm (x)dx, a                                                (25)

1 ^b

Gm =     A (x,0)Фm (x)dx, to mja

где a = - 1 1 , b = 1 2 , , , d A(x , t)

A 1 ( xt ) =^.

В случае однонаправленного пучка

dA (x, 0)      dA (x, 0)

dt             dx’ тогда c b dA(x,0), ,

G^m =--f—— ^Ф m ( x ) d x .

to m ad

Вычисляя интеграл (27) по частям, получаем:

Gm =-^_(a(b,0)Фm (b)-A(a,0)Фm (a)-to m

b

^- j A ( x , ⁰ )

a

дФ m ( x ) ) dx .

д x       I

Для поля (2), которое в начальный момент времени сосредоточено между диэлектрической пластиной и левым зеркалом резонатора (т.е. A ( a , 0) = A ( b , 0) =0), выражение (28) упрощается:

Рассмотрим распространение в резонаторе с диэлектрической пластинкой импульса следующего вида:

c- [Ja (x, 0)^ dx ).

^to m V a            ^x^

F (x ) = F0

cos ( k ₀ ( x - x ₀ ) ) exp

(x - x 0)

^^^^^^B ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^B

2 g ²

.

В случае, если входное поле сосредоточено в первой области вдали от зеркал, базисные функции имеют вид, аналогичный (23):

Ф m ( X ) = P m Sin ( k m ( X + 1 1 ) ) .

С учётом узости входного поля пределы интегрирования можно расширить на всю числовую ось, тогда коэффициенты вычисляются по формулам:

F^m = P m J A ( x ,0 ) sin ( k m ( x + 1 1 ) ) d x ,

G m = P m J A ( x ,0 ) cos ( k m ( x + 1 1 ) ) d x ,

b m = i™" J A ( x ,0 ) exp ( - ik m ( x + 1 1 ) ) d x .          (32)

На рис. 5 показано распространение импульса (33) при x ₀ = -15 мкм, g = 3 мкм.

По результатам, представленным на рис. 5, хорошо видно, что при прохождении импульса через диэлектрическую пластинку частота осцилляций в области пластинки повышается в соответствии с относительным показателем преломления пластинки к окружающей среде. Также хорошо видно, что отражённый от пластинки сигнал фактически соответствует производной исходного импульса по времени. Отметим, что дифференцирование импульсов возможно также с использованием волноводных периодических структур и решёток [25 – 27], резонаторов [28], фотонных кристаллов [29], метаповерхностей [30, 31].

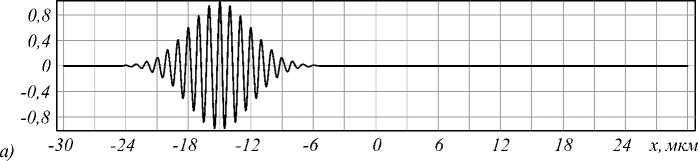
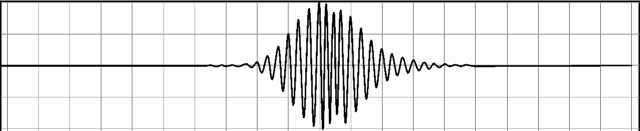
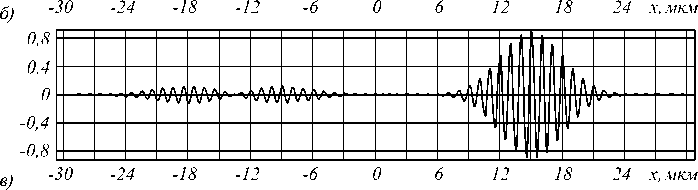
Рис. 5. Распространение импульса (33) при x o = -15 мкм, ст 3 мкм в резонаторе с диэлектрической пластинкой толщиной d=2 мкм и показателем преломления n=1,5 в различные моменты времени: t=0 (а), t=50 фс (б), t=100 фс (в)

3. Квантование поля в резонаторе с диэлектрической пластиной

Общая процедура квантования электромагнитного поля в резонаторе с диэлектриком описана во многих работах [5–9, 32].

Перепишем выражение для векторного потенциала в виде

A (x, y, z, t) = £ CsMs Ф s (x, y, z) exp (-ito st) + s                                      (34)

+ c s M s Ф S ( x , y , z ) exp ( i to s t ) ,

где c s – произвольные постоянные, M s – константы, которые определяются в процессе квантования поля.

Запишем выражение для энергии (гамильтониана электромагнитного поля):

w =

A

1 .           <^j^2         Л

— f e( x, y, z ) — +(rot A)

8nJ v      \at) v ’

V                          J

d x d y d z ,    (35)

где s ( x , y , z ) - распределение диэлектрической проницаемости.

Используя ортогональность модовых функций, получаем выражение для гамильтониана в виде:

W ~ ^ r s ( e s c * + c s c s ) , s

Операторы рождения и уничтожения действуют в этом пространстве функций:

где r s – коэффициенты, зависящие от конкретной конфигурации оптической системы (некоторые примеры рассмотрены ниже).

Далее заменяем числовые константы на операторы, действующие в гильбертовом пространстве. В результате выражение для гамильтониана становится также оператором, действующим в том же пространстве:

W ~ ^ r s ( a s a s + a + a s ) .

s

Тогда выражение для оператора магнитного потенциала

A (x, y, z, t) = ^ asMs Ф s (x, y, z) exp (-ito st) + s                                      (38)

+ a + M s Ф - ( x , y , z ) exp ( i to s t ) .

Операторы электрического поля и магнитного поля имеют по аналогии с классической электродинамикой вид:

1 dA c d1 ’

H = rot A .

Можно показать, что операторы как функции координат и времени удовлетворяют уравнениям Максвелла.

Операторы a s и as⁺ , а также числа M s выбираются таким образом, чтобы оператор векторного потенциала удовлетворял уравнению

d A d 1

= { [ H , A ] ,

an й+ _ an

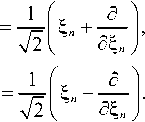
При таком выборе операторов выполняются коммутационные соотношения:

а+а —а а ⁺ =8 nm mn nm ^.

Очень полезным свойством операторов рождения и уничтожения является следующее:

Л( * ’ ( 5 ) a ■ /⁽- ) ) ^( x Cti a Ф - ( 5 ) ) d 5 ,

£ (ф * ^(-) a х^(-) ) d ^-=£ ( х⁽⁵⁾ a ⁺ф * ^(-) ) d ^- ,

где х ( — ) и Ф ( — ) — произвольные дифференцируемые функции.

3.2. Состояния с определённым числом фотонов

Рассмотрим базисные функции вида:

Ф q i q 2 ... q ,.... ( 5 i - 2 ...5р.. ) = П ф q n ( 5 n ) ,                    (49)

Ф q. ( 5 n ) = NH ( 5 n ) exp M n -) ,               (50)

где H_q n ( 5 n ) - полином Эрмита, N_n- нормировочный множитель, так что выполняется свойство ортонор-мированности:

( 'Ф q n ( 5 n ) Ф q „ ( 5 n ) d - n = 1.                            (51)

а гамильтониан электромагнитного поля имел вид

W = ^ htos | a+as + — |.(42)

s X

Для этого достаточно положить, что коммутаторы операторов имеют вид:

[as,a+] = 8sP,(43)

[ as, ap ] = [ as, a + ] = 0.(44)

• 3.1.    Пространство состояний электромагнитного поля

Пространство состояний электромагнитного поля описывается пространством функций бесконечного числа переменных:

Ф ( 5& ...5 j ... ) .                                          (45)

Каждая переменная в (45) относится к отдельной моде, причём переменные не связаны с пространственными координатами.

Операторы (46) действуют в этом пространстве следующим образом:

a n ^Ф q n ( ⁵ n ) = V q n ^Ф q n -I ( ⁵ n ) , ^{a + Ф} q n ( ⁵ n ) = V ( q n ^{+ 1} ) ^Ф q n +1 ( ⁵ n ) , ^an^an ^Ф q n ⁽⁵ n ) = ⁽ q n ^{+ 1 )Ф} q n ( ^ n ) , a + a n Ф q n ( 5 n ) = q n Ф q n ( 5 n ) •

Рассмотрим действие оператора Гамильтона на базисную функцию (49):

H Ф q 1 q 2_.. ( 5 1 5 2 ...5 j ... ) =

• 3.3.    Когерентные состояния квантового поля в резонаторе

Когерентные поля описываются функциями состояния вида:

4' n (^n ) = exp (-an/2)^^L Ф m (^n).(56)

m !

Действие оператора:

anWn (^n ) = anWan (^n ),(57)

a. Т..- „((j(58)

= « n W a i a₂...a,... (i ; ii ; 2 -Л-. ) .

• 3.4.    Сжатые состояния

Сжатые состояния определяются следующим образом:

|a,^ = S (^) D (a)| 0),(59)

где a и ^ - произвольные комплексные числа,

D ( a ) = exp ( a a ⁺ -a * a ) =

Г „I2 ^

a        (. X

= exp - ^L"2- exp ( a a ⁺ ) exp ( -a a ) =

= exp

exp ( -a * a ) exp ( a a ⁺ ) ,

Г 1              1

^S ( ^ ) = exp I 2 ^ * a 2 ^- 2 ^ ( a + )

Для вычисления средних значений нам понадобятся следующие формулы

(a , ^1 a | a , ^ = (a , ^1 D ⁺ ( a ) S ⁺ ( £ ) aS ( £ ) D ( a)| 0^ =

= (al a ch ( r ) - a ⁺ exp ( i 9 ) sh ( r )| a)=                (62)

= a ch (r )-a* exp (i 9) sh (r), где было использовано представление ^ = r exp (i9).

(a , £l a ²1 a , ^ =

= (a , ^| D ⁺( a ) S ⁺(y a ² S ( ^ ) D ( a )| 0) =

= (a , ^| D ⁺ ( a ) S ⁺ ( ^ ) aS ( ^ ) S ⁺ ( ^ ) aS ( ^ ) D ( a ) | 0) = (63)

= a ²ch² ( r ) + ( « *) 2 exp ( 2i 9 ) sh² ( r ) -

- 2| a| 2 exp ( i 9 ) sh ( r ) ch ( r ) - exp ( i 9 ) sh ( r ) ch ( r ) .

(a , £l a ⁺ a |a, ^ = |a| 2 ( ch² ( r ) + sh² ( r ) ) -

- ( a * ) 2 exp ( i 9 ) sh ( r ) ch ( r ) -                        (64)

- ( a ) 2 exp ( - i 9 ) sh ( r ) ch ( r ) + sh² ( r ) .

• 3.5.    Перепутанные состояния

Рассмотрим две моды резонатора с номерами n и m . Пусть в моде n содержится n n фотонов, а в моде m содержится n m фотонов.

Состояние описывается следующей функцией:

Ф^n§m ) = Фnn (^n )Фnm (^m ) ,(65)

где Ф q_n ( ^ n ) описывается выражением (50).

Рассмотрим ещё две моды резонатора с номерами p и s , содержащие n p и n s фотонов соответственно:

Ф(^ p^^ ) = Ф ns (^S )Ф np (^p ).(66)

Далее рассмотрим состояние:

Ф ( § n ^ m ^ p ^ s ) =

= ^= (Фnn (^n )Фnm (^m ) + Фns (^s )Фnp (^p )).

Состояние вида (67) нельзя представить с помощью функции с разделяющимися переменными. Такие состояния называются несепарабельными (неразделимыми) или перепутанными состояниями.

Другим примером перепутанного состояния может служить вариант, когда перепутываются две моды:

Ф ( § n ^ m ) =

= -12 ( Ф n n ( ^ n ) Ф n m ( ^ m ) + Ф n m ( ^ n ) Ф n n ( ^ m ) ). ^

• 4. Вычисление наблюдаемых величин

Наблюдаемое значение любой физической величины в квантовой механике определяется средним значением оператора этой величины и вычисляется по формуле p = !(ф*( x) P (x )Ф( x)) dx.

Для описания распространения поля в квантовой трактовке необходимо вычислить средние значения оператора электрического поля. Оператор электрического поля выражается через оператор векторного потенциала

, .     1 dAU, A

E ( r , t ) = ^x c d t

Наблюдаемое значение электрического поля – это среднее значение оператора электрического поля

E 0 ( r , t ) = (W| E ( r , t )| W> .

где | W) описывает состояние квантового электромагнитного поля.

Среднеквадратичные отклонения электрического поля

( A E 0 ( r , t ) ) 2 = (V| ( E ( r , t ) - E 0 ( r , t ) ) ²| V) .          (72)

В дальнейшем нас будут интересовать также операторы положительно-частотной части электрического поля E ⁽⁺⁾ ( r , t ) и оператор отрицательно-частотной части электрического поля E ^(–)( r , t ) и их матричные элементы

E 0 ⁺⁾ ( r , t ) = (Y| E ⁽⁺⁾ ( r , t )|V) , E < ^-) ( r , t ) = (Y E »( r , t )|Y> .

Для расчёта наблюдаемых величин нам будет необходимо найти квадраты электрического поля

( E ^: ( r , t ) E ⁽⁺⁾ ( r , t )) =

= (ф E ^(-) ( r , t ) E ⁽⁺⁾ ( r , t )|ф) .

Эти выражения соответствуют наблюдаемым величинам, которые измеряются в эксперименте.

• 4.1.    Вычисление средних значений векторного потенциала

Однако следует отметить, что среднее значение оператора квадрата электрического поля не равно нулю.

В когерентном состоянии

Рассмотрим одномодовое когерентное состояние

I ^a m 1У^(а m )

|Vm) = expl —— 1Л      |П”)•

< 2)

Многомодовое когерентное состояние

IY m)=W-)•(80)

m это состояние удовлетворяет соотношению am| V m) = am| Ym) •

Для сопряжённого оператора выполняется соотношение

(Y{ m} |am=(Y m I am.(82)

Эти два уравнения позволяют вычислять матрич-

A ( x, y, z, t ) =

= £ a m M Ф m ( x , y , z ) exp ( - i to m t ) +              (76)

+ a m M m Ф ” ( x , y , z ) exp ( i to m t ) .

ные элементы операторов.

I V = H = n| a n ),

n

(Y| a m |v} = (a| a m |a) = a m •

Среднее значение оператора

(Y| A ( x , y , z , t )|v) =

= £( ф I a m | y) M m Ф m ( x , y , z ) exp ( - i to m t ) +      (77)

+X(v M V M m ^Ф ” ( x , y , z ) exp ( i to m t ) •

При вычислении (77) используется соотношение:

*

(V | a m |Y) = ((Y | a m | V)) .

В состоянии с определённым числом фотонов

Рассмотрим состояние | n_m ) с определённым числом фотонов в моде c номером m . Эти состояния удовлетворяют соотношениям

Например, найдём среднее значение оператора электромагнитного потенциала в когерентном состоянии.

(Y| A ( x , y , z , t )| Y) =

= ^ a m M m Ф m ( x , y , z ) exp ( - i to m t ) +              (85)

+ a ” M m Ф ” ( x , y , z ) exp ( i to m t ) •

Это выражение совпадает с функцией векторного потенциала в классической теории. То же самое можно сказать относительно операторов электрического и магнитного полей.

В сжатом когерентном состоянии

В этом случае:

a m| n m ) = T n ” |( П ” — 1)) , a ” | n m ) = V П ” + 1 | ( П ” + 1)) •

I Y) = |a,n) = n| a n ,n « ) = |a m ,П m )H|a n ,П n \   (86)

n                           n ^ m

Учитывая соотношение в (86), получаем:

В случае многомодового поля в резонаторе состояние электромагнитного поля описывается вектором

I V = | n m ) = №) ,

(Y| a m |Y) = ^| a m |^ = 0.

В результате получаем, что среднее значение магнитного потенциала и электрического поля в состоянии с определённым числом фотонов равно нулю.

(Y| a m |v) = (a,n| a m |a,n) =

= H( a n ,П n I I a n ,n n ) (a m ,n m | a m |a m ,n m ) =        (87)

n ^ m

= (a m ,n m| a m |a m ,П m )•

Далее, используя выражение (62), получаем

(a m , ^ m|a,

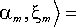
= a m ch ( r m ) -a m exp ( i 9 m ) sh ( r m ) •

Особенность сжатых состояний

Рассмотрим простой случай

A ( X , y , z , t ) = £ a M m Ф m ( X , y , Z ) exp ( - i to m t ) + + a m M m Ф т ( X , y , z ) exp ( i to m t ) .

Пусть у нас есть только одна мода

A ( X , y , Z , t ) = a m M m Ф m ( X , y , Z ) exp ( - i to m t ) + + a m M m Ф m ( X , y , z ) exp ( i to mt ) .

Оператор электрического поля имеет вид

E ( x , y, z, t ) =

= ia m I ^^ M m |^Ф m ( X , y , z ) exp ( - i to mt ) -

только оператором Y 1 , в другой момент времени – только оператором Y 2 .

Дисперсии этих операторов, а значит, и дисперсии электрического поля равны

( DY ) 2 = YY ,²) - Y )² = 4exp ( 2 r ) , ( DY ₂ ) 2 = YY ₂²) - YY^ = 4exp ( - 2 r ) .

В результате получается, что дисперсия в одни моменты очень большая по сравнению с когерентным состоянием, но зато в другие моменты дисперсия электрического поля намного меньше, чем в когерентном состоянии.

В перепутанном состоянии

- ia m I — M m |ф m ( X , y , z ) exp ( i to m t ) .

Обозначим Q_m =

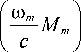
| Ч^Ф^ n ^ m ^ p ^ s ) =

= ^= ( Ф „ „ ( ^ n ) Ф n m ( ^ m ) + Ф n s ( ^ s ) Ф n p ( ^ p ) ) ,

(Y|aq |Y) =

Введём новые операторы рождения и уничтожения:

ia m b m ,

- ia m = b m ,

E ( X , y , z , t ) = b m Q m Ф m ( X , y , z ) exp ( - i to mt ) + + b m Q m Ф * m ( X , y , z ) exp ( i to m t ) .

Ф m ( x , y , z ) являются действительными функциями.

E ( X , y , z , t ) =

= Q m Ф m ( X , y , z ) ( b m eXp ( - i to m t ) + b m eXp ( i to m t ) ) .

Представим выражение в виде

E ( X , y , z , t ) =

= 2 Q m Ф m ( X , y , z ) ( X i SO S ( to m t ) + X 2 sin ( to m t ) ) ,

( b m + b m ) __.( b m - b m )

X i =-----------; X ? = i.

Рассмотрим теперь f9)f

X, = Y cos    - Yq sin,

• 11    12 J 2

f®)f®)

X2 = Y sin    + Y2 cos.

• ²¹    I 2 J ² I 2 J

  
  
  
  

Подставляя это в выражение для электрического поля, получаем

E ( x , y , z , t ) =

= 2 (Ф n n ( ^ n ) Ф n m ( ^ m ) + Ф n s ( ^ s ) Ф n p ( ^ p ) x

X a q ( ^ q )|Ф n n ( ^ n ) Ф n m ( ^ m ) + Ф n s ( ^ s ) Ф n p ( ^ p )) =

= (Ф nn (^n )Ф nm (^m )| aq (^q )|Ф nn (^n )Ф nm (^m ))+ (102)+ (Фnn (^n )Фnm (^m )| aq (^q )| Фns (^s )Фnp (^p )) +

+ (Ф n s ( ^ s ) Ф n p ( ^ p )| a q ( ^ q )| Ф n n ( ^ n ) Ф n m ( ^ m )) +

+ (Фns (^s )Фnp (^p )| aq (^q )|Фns (^s )Фnp (^p )) .

Найдём действие оператора на базисные вектора:

a q ( ^ q )| Ф n s ( ^ s ) Ф n p ( ^ p )) = = 8 qsjn^ |Ф n s -1 ( ^ s ) Ф n p ( ^ p )) + + 5 qp^ n p |^Ф n s ( ^ s ) ^Ф n p -1 ( ^ p )) , a q ( ^ q )| Ф n n ( ^ n ) Ф n m ( ^ m )) = = ⁵ qs^fnn |^Ф n n -1 ⁽^ n ^)Ф n m ⁽^ m )^ ⁺ +5 qnX n m |Ф n n ( ^ n ) Ф n m -1 ( ^ m )} .

Используя соотношение

(Ф n s ( ^ s ) Ф n p ( ^ p )| Ф n n ( ^ n ) Ф n m ( ^ m )) = 5 sn 5 pm , (105)

можно получить явный вид для {^ | a q | V) .

Заключение

= 2 Q m Ф

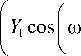
9), _v _ 2 1 + Y 2 sin Ito m t

Из этого выражения видно, что в одни моменты времени оператор электрического поля определяется

На примере дифракции света на диэлектрической пластине в резонаторе рассмотрены аспекты квантовой оптики. Показана связь между классическим и квантовым решением задачи дифракции на диэлектрической пластине. Получены выражения для соб-

ственных мод такого резонатора, а также для операторов векторного магнитного потенциала и напряжённости электрического поля. Метод, предложенный в данной работе, может быть распространён на диэлектрические пластины с дифракционным микрорельефом, то есть на дифракционные оптические элементы. Результаты расчёта квантовых систем с дифракционными оптическими элементами будут представлены в следующих публикациях.

Работа выполнена при финансовой поддержке Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части анализа дифракции излучения в резонаторе на диэлектрической пластине, а также в рамках реализации Программы развития Самарского университета на 2021–2030 годы в рамках программы «Приоритет-2030» при поддержке Правительства Самарской области в части разработки квантовой теории дифракционных оптических элементов.