Расчет манипуляторов с гидравлическим приводом в машинах различного технологического назначения

The summary. In article calculation of manipulators with a hydraulic drive in machines of various technological appointment by means of the mathematical method based on use of a matrix of turns and a vector of movings is considered

Формирование эффективных уравнений динамики манипуляторов технологических машин, которые могут быть рассчитаны на ЭВМ, является одной из важнейших задач в машиностроении. Ее решение необходимо для моделирования динамики манипуляторов в масштабе реального времени, для разработки эффективных алгоритмов управления технологическими машинами с учетом динамики, для повышения эффективности исследования и разработки манипуляторов.

Одним из методов математического моделирования манипуляторов является способ расчета кинематических и динамических величин, определяющих математическую модель манипулятора [1,2]. Для этого используются матрицы поворотов размерности 3x3 и вектора относительных перемещений.

Рассмотрим 3-звенный манипулятор с вращательными шарнирами (рис.1). Для описания его кинематики с каждым из звеньев сформируем систему координат, относительно которой будут рассчитываться параметры звена, а также введем обобщенные координаты, т.е. зададим направления отсчета углов поворота звеньев.

С основанием манипулятора П₀ свяжем неподвижную систему координат (СК) S 0 , причем одна из ее осей совпадает с осью первого поворота e rot 1 , а начало находится в центре первого шарнира - точке О 1 .

Теперь построим систему координат S 1 , связанную с первым звеном П 1 . Ее начало выберем в центре первого шарнира. Одну из координатных осей СК S 1 направим по оси первого поворота. Так как ось поворота второго звена e rot 2 ⊥ e rot 1 , то одну из осей в плоскости, перпендикулярной e rot 1 , направим параллельно вектору e_{rot 2} , а третья координатная ось будет дополнять выбранные две до правой ортогональной тройки.

Таким образом, как СК S₀ и S₁, так и СК S₁ и S₂ будут иметь одну координатную ось с общим направлением, определяемым для S₀ и S₁ вектором e_{rot 1} , а для S₁ и S₂ вектором e_{rot 2} . Поэтому матрицы перехода от S 0 к S 1 и от S 1 к S 2 будут матрицами поворотов относительно соответствующих координатных осей : ξ _i ∈ { ξ _x, ξ _y, ξ _z}, где ξ _x, ξ _y, ξ _z - матрицы поворотов относительно осей x , y и z соответственно.

Аналогичным образом определим системы координат S 2 , S 3 оставшихся звеньев манипулятора (S i связана со звеном П i , а ее начало O i находится в центре i-ого шарнира).

Для однозначного определения СК S 1 , .., S n необходимо задать направления отсчета обобщенных координат q 1 , .., q n (q i определяет переход от S_i-1 к S_i). С этой целью введем вектора e⁰_qi ∈ П i-1 (направлен по одной из координатных осей СК S i-1 , перпендикулярных e_{rot i} ) и e¹_qi ∈ П_i (направлен по одной из координатных осей СК S i , перпендикулярных e rot i ).

Угол q_i будем отсчитывать от e_qi⁰ к e_qi¹ ; положительное

01 направление отсчета определяется поворотом от e_qi к e_qi

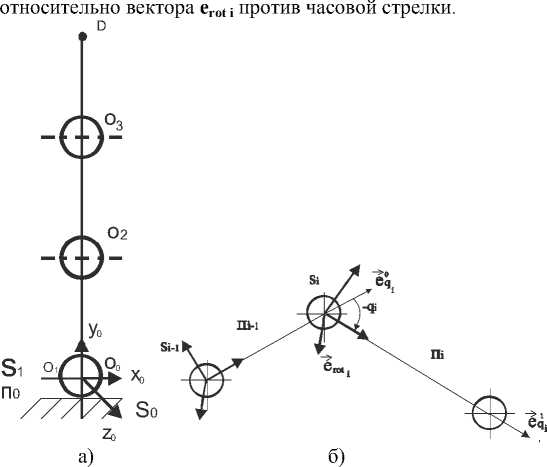
Рис.1. Расчетная схема манипулятора

Для полного кинематического описания манипулятора необходимо определить матрицы поворотов ξ i , задающие ориентацию соседних систем координат S_i-1 и S_i, и вектора переноса l_i-1 = O_i-1O_i, определяющие сдвиг между ними (l₀ = 0, т.к. O 0 = O 1 ; l n = O n D, где D - конечная точка манипулятора).

Для манипулятора в “начальном” состоянии, т.е. при q 1 = q 2 = ... = q n = 0. Задав СК S 0 (т.е. оси координат х 0 , y 0 , z 0 ), выполним последовательно параллельные переносы S 0 в точки O 1 , O 2 , ..., O n .

При этом будут определены оси систем координат S 1 , ..., S n . и матрицы ξ _i и вектора l_i. для каждого звена.

Затем, при q1 = q2 = ... = qn = 0, найдем направления осей СК звеньев (рис.1) В соответствии с рисунком определены матрицы ξi и вектора li: ξ1 = ξy, ξ2 = ξ3 = ξz, l1 = (l1x;0;0); l2 =(l2x;0;0); l3 =(l3x;0;0)

(l ix , l iy , l iz определяют геометрические размеры звеньев).

Далее получены основные соотношения кинематики манипулятора.

Координаты точки D (выходное звено манипулятора-ударник) могут быть найдены из соотношения:

nn

R D = ∑    l i⁰ = ξ 1 ξ 2 l 1 + … + ξ 1 ξ 2 … ξ n l n = ∑   ξ 1i l i

i=1                                      i=1

где принято обозначение ξ _1i = ξ ₁ ξ ₂ … ξ _i l i⁰ - координаты вектора l i в СК S 0 .

Матрица ξ _D = ξ _1n определяет ориентацию точки D в СК (совпадающую с СК S_n) относительно базовой СК S₀. Пара (R_D, ξ _D) задает решение прямой задачи кинематики манипулятора.

Линейная скорость ударника определяется выражением:

VD = RD′ = (ξ1′ξ2 + ξ1ξ2′)l1 +...+( ξ1′ξ2...ξn+..+ ξ1ξ2…ξn′)ln (здесь учтено, что li′ = 0, т.к. эти вектора рассматриваются относительно неподвижных систем координат).

Производные от матриц поворотов можно вычислить с помощью вспомогательных матриц Q i :

ξ i ′ = Q i ξ i q i ′

Введя обозначение: V ps = ξ 1 ξ 2 ... ξ s-1 Q s ξ s ... ξ p

Получим:

n

( ∑  Vps lp) qs′ p=s

V D = V 11 q 1 ′ l 1 +...+ (V n1 q 1 ′ +...+ V nn q n ′ ) l n = ∑ ⁿ

s=1

Угловая скорость конечного звена манипулятора по теореме сложения угловых скоростей равна геометрической сумме угловых скоростей звеньев:

nn   n

WD = ∑  WS = ∑  erot s0 qs′ = ∑ ξ1s erot s qs′ s=1        s=1            s=1

Далее можно определить матрицу Якоби манипулятора. По определению матрица Якоби манипулятора J(q) связывает вектора V D и W D с вектором обобщенных координат манипулятора q = (q 1 , q 2 , ..., q n ) ^T :

(V d , W d ) = J(q) q '

Определим компоненты матрицы Якоби:

n

J vs = X   V ps i p ;

p=s

Jws = ^1s erot s где Jvs - компоненты первых трех строк матрицы Якоби, Jws -компоненты последних трех строк.

В дальнейшем, при выводе уравнений динамики манипуляторов, используются также выражения для радиус-вектора R i и скорости V i произвольной точки M i i-ого звена манипулятора:

Для вывода уравнений динамики манипулятора используется описание кинематики с помощью матриц поворотов и векторов переноса и уравнения Лагранжа II рода:

d Г dL)  dL

= ^Tk

d (dqk J  -\     k

где L = (K - P) - функция Лагранжа, K и P - кинетическая и потенциальная энергия манипулятора; т _к - момент обобщенных сил в k-ом шарнире, обусловленный работой привода и воздействием внешних нагрузок.

Чтобы воспользоваться уравнениями Лагранжа, необходимо вычислить кинетическую и потенциальную энергию манипулятора.