Расчет методом потоков структуры течения и аэродинамических характеристик при отделении лобового теплозащитного экрана от возвращаемого аппарата

Всовременныхкосмическихвозвращаемых аппаратах (ВА) применяются лобовые теплозащитные экраны (ЛТЭ), отделяемые от возвращаемого аппарата на малых дозвуковых скоростях на режиме посадки. Наличие в набегающем потоке теплозащитного экрана вблизи ВА существенно влияет на структуру течения и аэродинамические характеристики ВА. Учет этого влияния необходим при проектировании систем отделения ЛТЭ.

Математическое моделирование обтекания ВА вместе с ЛТЭ может осуществляться на основе нестационарной модели невязкого сжимаемого газа, позволяющей моделировать крупномасштабные вихревые структуры, предполагая, что вязкость и мелкомасштабная турбулентность не оказывают существенного влияния на основные характеристики потока. Несмотря на указанное упрощение математической модели, подобный подход в трехмерной нестационарной постановке требует использования значительных вычислительных мощностей и больших временных затрат.

В настоящей работе задача об обтекании ВА и ЛТЭ решается в пространственно-нестационарной постановке на основе консервативного численного метода, реализованного на суперкомпьютере кластерной архитектуры. Рассматривается влияние различных расположений ЛТЭ по отношению к ВА на структуру пространственно-нестационарного потока и аэродинамические характеристики ВА и ЛТЭ.

Постановка задачи. Численный метод

Рассматриваются ВА и находящийся неподвижно около него ЛТЭ (рис. 1).

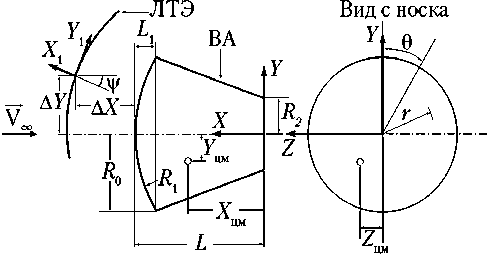
Рис. 1. Схематизация возвращаемого аппарата (ВА) и лобового теплозащитного экрана (ЛТЭ). Система координат

Примечание. L — длина аппарата; L ₁ — высота лобовой сферической поверхности; R ₀ — радиус миделя аппарата.

ВА представляет собой тело вращения, состоящее из лобовой сферической поверхности, конической боковой поверхности с углом полураствора 20 ° и донного среза. ЛТЭ представляет собой сферический сегмент, совпадающий по форме и размерам с лобовой сферической поверхностью ВА. Используются две правосторонние системы координат ОХYZ и О ₁ Х ₁ Y ₁ Z ₁, связанные соответственно с ВА и ЛТЭ (рис. 1).

Меридиональные углы 0 и 6 1 отсчитываются от положительных направлений соответственно осям OY и O ₁ Y ₁ против часовой стрелки.

Взаимное расположение ВА и ЛТЭ задается значениями Ах, А у — расстояниями вдоль осей ОХ и ОY между центром лобовой сферической поверхности ВА и центром поверхности ЛТЭ, а также значением v — угла поворота ЛТЭ вокруг оси O 1 Z 1. Влияние разворота ЛТЭ вокруг оси O1Y1 не рассматривалось.

Рассматриваемая среда — идеальный газ с отношением удельных теплоемкостей Y = 1,4 и параметрами стандартной атмосферы на бесконечности. Вектор скорости набегающего потока направлен вдоль отрицательного направления оси ОХ (угол атаки ВА равен нулю). Число Маха набегающего потока M_∞ = 0,2.

В дальнейшем используются безразмерные единицы, в которых линейные размеры отнесены к радиусу миделя ВА R ₀, плотность, скорость и температура отнесены соответственно к плотности, скорости и температуре набегающего потока. Время отнесено к R ₀/ V _∞, где V _∞ — скорость набегающего потока. Значения геометрических размеров ВА следующие:

Длина аппарата L , м                    1,732;

Высота лобовой сферической поверхности L ₁, м                       0,275;

Радиус кривизны лобовой сферической поверхности R ₁, м         1,953;

Радиус донного среза R ₂, м              0,471.

Координаты центра масс возвращаемого аппарата ( Х _цм, У _цм, Z _цм) принимались равными

Х _цм / L = 0,65; У _цм / L = –0,04; Z _цм / L = 0,00.

Решение задачи осуществлялось на основе нестационарного варианта консервативного метода потоков [1, 2], основанного на конечноразностной аппроксимации законов сохранения, записанных в интегральной форме для каждого конечного объема вычислительной сетки. Разработанные параллельные алгоритмы [3, 4] реализованы на вычислительном комплексе кластерной архитектуры Межведомственного суперкомпьютерного центра Российской академии наук (МСЦ РАН). В расчетах использовалось до 1 500 процессоров.

Результаты расчетов

В настоящей работе исследовалось влияние относительных расстояний А х , А у , угла V на структуру потока и аэродинамические силы, действующие на ВА и ЛТЭ. В расчетах использовались вычислительные сетки, включающие до 5∙10⁶ расчетных объемов. Фрагмент вычислительной сетки представлен на рис. 2.

В качестве начальных данных в момент времени t = 0 задается невозмущенный дозвуковой поток, в который помещены ВА и ЛТЭ. Скорости газа в области между ними и в донной области ВА при t = 0 принимались равными нулю.

Рис. 2. Фрагмент вычислительной сетки

а)

Общие характеристики течения

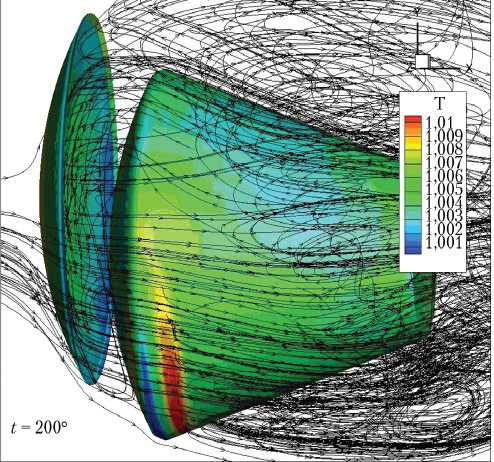
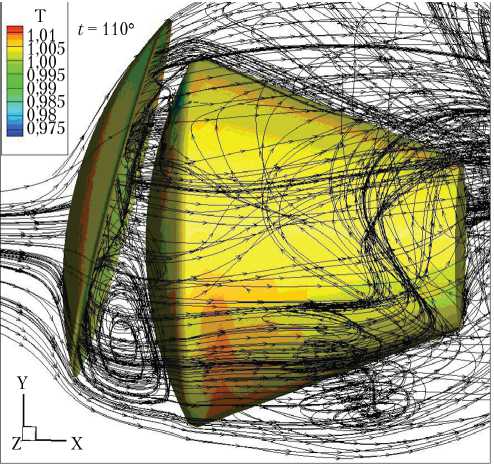
При симметричном расположении теплозащитного экрана по отношению к ВА численное решение сначала имеет симметричный характер, который при дальнейшем интегрировании теряет устойчивость, и течение приобретает пространственно-нестационарный характер, переходящий в устойчивый, но нестационарный режим. При несимметричном расположении ЛТЭ по отношению к ВА численное решение с момента времени t = 0 пространственно-нестационарно. В качестве примера, демонстрирующего сложную структуру течения, на рис. 3 изображены мгновенные линии тока для А х = 0,4; А у = 0,3 и двух значений угла у = 0 ° и у = 15 ° . Здесь же цветом показано распределение безразмерной температуры газа по поверхности ВА.

На рис. 4 показаны зависимости от времени t на установившемся режиме аэродинамических характеристик ЛТЭ, а именно, коэффициента подъемной силы C y _а , коэффициента боковой силы C z _а , коэффициента момента тангажа M в случае А х = 0,4; А у = 0,3; V = 10 ° .

В дальнейшем приводятся аэродинамические характеристики, усредненные по достаточно большому промежутку времени на установившемся режиме. Моменты аэродинамических сил, действующие на ВА, рассчитаны относительно его центра масс, а моменты сил, действующие на ЛТЭ, — относительно начала координат ( О ₁ X ₁, Y ₁, Z ₁). При вычислении коэффициентов моментов сил, действующих на ВА и ЛТЭ, значения моментов относились к скоростному напору набегающего потока, площади миделя (одинаковой для аппарата и экрана) и, соответственно, длине L или L ₁.

б)

Рис. 3. Мгновенные линии тока для случая А х = 0,4; А у = 0,3: а — у = 0 ° ; б — у = 15 °

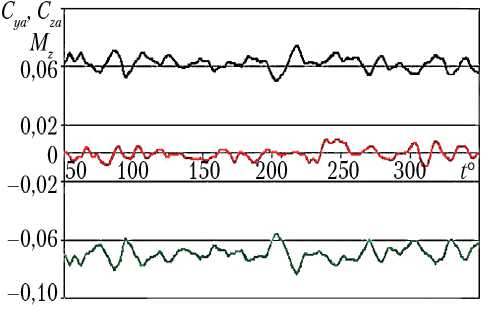
Рис. 4. Зависимость коэффициента подъемной силы C y _а , коэффициента боковой силы C z _а , коэффициента момента тангажа M_z от времени t для лобового теплозащитного экрана для случая А х = 0,4; А у = 0,3; у = 10 ° Примечание. — — C y _а ; — — C z _а ; — — M z .

Влияние смещения ЛТЭна аэродинамические характеристики

В табл. 1, 2 приведены суммарные аэродинамические характеристики ВА и ЛТЭ (коэффициенты лобового сопротивления C x _а , подъемной силы C y _а , момента тангажа M z ) для различных значений А х , А у , v .

Значения коэффициентов С х _а , С у _а , M z для возвращаемого аппарата

Значения коэффициентов С х _а , С у _а , M z для лобового теплозащитного экрана

Таблица 1

А х	А У	v°	C ха	C У а	M z
0,2	0	0	–0,523	–0,00069	–0,0209
0,3	0,2	0	–0,270	0,06509	–0,0426
0,3	0,2	10	–0,326	0,03236	–0,0328
0,4	0,3	0	–0,118	0,06915	–0,0500
0,4	0,3	10	–0,107	0,01635	–0,0349
0,4	0,3	15	–0,122	–0,01932	–0,0387
0,6	0,4	10	–0,056	0,00797	–0,0488
0,6	0,4	20	–0,085	–0,01279	–0,0645

Таблица 2

А х	А У	v°	C ха	C У а	M z
0,2	0	0	1,665	–0,00031	0,0022
0,3	0,2	0	1,464	0,02701	–0,1898
0,3	0,2	10	1,455	0,05083	–0,3572
0,4	0,3	0	1,382	0,03811	–0,2679
0,4	0,3	10	1,286	0,06000	–0,4216
0,4	0,3	15	1,265	0,07261	–0,5099
0,6	0,4	10	1,228	0,06216	–0,4366
0,6	0,4	20	1,230	0,09769	–0,6865

Из табл. 1 видно, что во всех рассмотренных случаях значения коэффициента лобового сопротивления ВА отрицательны, что вызвано значительным разрежением в области между ЛТЭ и лобовой частью ВА. В этой области возникает интенсивное вихревое течение (см. рис. 3). В качестве примера на рис. 5, 6 показаны зависимости коэффициента давления

Ср = 2(Р- РJ /(YMJPJ от меридионального угла 0 на лобовой сферической поверхности ВА для трех значений угла наклона ЛТЭ v = 0; 10; 15°, где Р„ — давление в набегающем потоке на бесконечности, Р — давление на поверхности.

На рис. 5 представлены данные на сферической поверхности в плоскости x = const для значения радиуса окружности r = 0,41, а на рис. 6 — для значений r = 0,83.

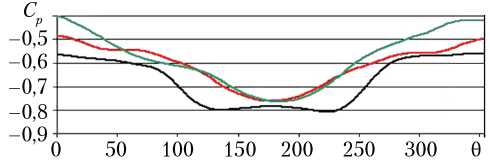
Рис. 5. Зависимость С р от 0 на сферической поверхности возвращаемого аппарата для случая А х = 0,4; А у = 0,3; r = 0,41 Примечание. ■ — v = 0 ° ; ■ — v = 10 ° ; ■■" — v = 15 ° .

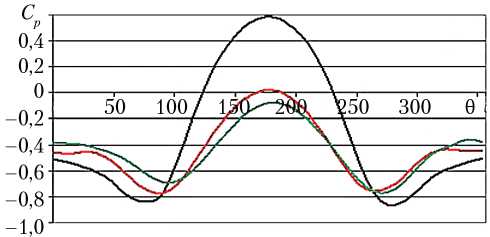
Рис. 6. Зависимость С_р от 0 на сферической поверхности возвращаемого аппарата для случая А х = 0,4; А у = 0,3; r = 0,83 Примечание. — — v = 0 ° ; ■■“ — v = 10 ° ; “ — v = 15 ° .

Из сравнения рис. 5 и 6 видно, что влияние угла наклона v на распределение С р ( 0 ) увеличивается при увеличении r . Так, на рис. 5 все три кривые достаточно близки между собой, в то время как на рис. 6 кривая, соответствующая v = 0 ° , заметно отличается от двух других. На нижней части сферической поверхности ВА появляется область, где разрежение сменяется областью повышенного давления.

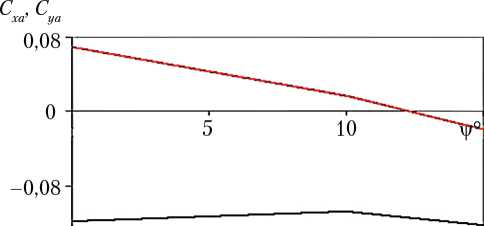
На рис. 7 показаны зависимости коэффициентов лобового сопротивления и подъемной силы ВА от угла наклона v при Ах = 0,4; А у = 0,3. Видно, что в этом случае сила лобового сопротивления практически не зависит от угла наклона теплозащитного экрана, а подъемная сила уменьшается с ростом v , что согласуется с данными, приведенными на рис. 5, 6.

-ОД6J-------------------------------------

Рис. 7. Зависимость С_{х а} и С_{у а} от v для возвращаемого аппарата для случая А х = 0,4; А у = 0,3

Примечание. ■ — C x _а; ■■" — C y _а.

Влияние угла наклона лобового теплозащитного экрана на его аэродинамические характеристики

Рассмотрено смещение ЛТЭ А х = 0,4; А у = 0,3. На рис. 8 показаны зависимости коэффициента давления C_р от меридионального угла 0 1 на поверхности ЛТЭ для трех значений v = 0; 10; 15 ° на окружности r 1 = 0,7.

Пунктирными линиями приведены данные для наветренной (лобовой) стороны экрана, сплошными — данные для подветренной (донной) стороны. Видно, что за ЛТЭ существует разрежение, которое слабо зависит от угла наклона экрана v при r 1 = 0,7.

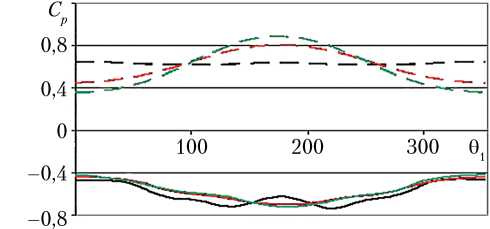
Рис. 8. Зависимость С р от 0 1 на поверхности лобового теплозащитного экрана для случая А х = 0,4; А у = 0,3; r 1 = 0,7 Примечание. ---; — — v = 0 ° ; ---; — — v = 10 ° ; ---; — — v = 15 ° .

Зависимости коэффициентов лобового сопротивления и момента тангажа ЛТЭ от его угла наклона для А х = 0,4; А у = 0,3 представлены на рис. 9, а на рис. 10 показана зависимость коэффициента подъемной силы от угла наклона при тех же значениях А х и А у .

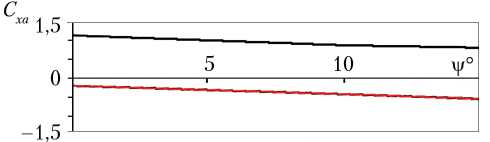
Рис. 9. Зависимость С_{х а} и M z от v для лобового теплозащитного экрана для случая А х = 0,4; А у = 0,3

Примечание. — — C x _а; — — М z .

Приведенные данные показывают, что ЛТЭ статически устойчив в исследованном диапазоне изменения углов v . Действующие на ЛТЭ аэродинамические силы при увеличении угла v стремятся уменьшить его величину. Сила лобового сопротивления экрана при этом незначительно уменьшается.

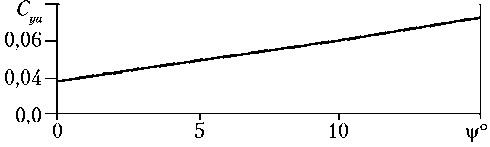
Рис. 10. Зависимость С_{у а} от v для лобового теплозащитного экрана для случая А х = 0,4; А у = 0,3

Заключение

Проведенные исследования показывают, что наличие отделяемого ЛТЭ вблизи ВА существенно влияет на их аэродинамические характеристики, что необходимо учитывать в анализе динамики разделения.

Аэродинамическое сопротивление ЛТЭ увеличивается примерно в 1,5 раза по сравнению с изолированным экраном, а сопротивление ВА становится отрицательным в результате изменения структуры течения между этими объектами, что может замедлять процесс их расхождения.

Взаимное влияние между ЛТЭ и ВА проявляется при достаточно больших расстояниях (до одного диаметра корпуса ВА), уменьшаясь с увеличением расстояния.

При появлении поперечных смещений на ЛТЭ и ВА действуют дополнительные возмущающие аэродинамические силы и моменты, которые необходимо учитывать при расчете траекторий их относительного движения.

Результаты настоящей работы, полученные для значения M∞ = 0,2, могут быть распространены и на другие малые дозвуковые скорости набегающего потока, поскольку на этих режимах аэродинамические характеристики слабо зависят от числа M . ∞