Расчет мод фотонно-кристаллического световода разными методами

Коммерческая программа моделирования процессов распространения света FIMMWAVE v.4.6 позволяет рассчитывать моды диэлектрических световодов с произвольным поперечным сечением однородных в продольном направлении, в том числе фотонно-кристаллических световодов (ФКС), с помощью реализации векторного метода согласованных синусоидальных мод (FMM Solver (real)) и метода эффективного индекса (Eff. Idx. Solver (real)).

Основной целью статьи является сравнение двух реализаций метода FMM c помощью программы FIMMWAVE 4.6 и программы в среде Matlab 7.0 для расчета мод ФКС.

Фотонно-кристаллические световоды – это относительно новый класс оптических волокон, использующих свойства фотонных кристаллов [1]. ФКС представляют собой кварцевую или стеклянную микроструктуру с периодической либо апериодической системой микровключений, чаще цилиндрических микроотверстий, ориентированных вдоль оси волокна. Дефект микроструктуры, соответствующий отсутствию одного или нескольких элементов в центре структуры, служит сердечником световода, обеспечивая волноводный режим распространения электромагнитного излучения. Существуют световоды со сплошным сердечником или сердечником с более высоким усредненным показателем преломления относительно микроструктурированной (дырчатой) оболочки, которые используют эффект полного внутреннего отражения, так же как и обычные оптические волокна, но в отличие от последних могут обладать лучшей способностью удерживать свет в сердечнике при его распространении за счет большей локальной разницы показателей преломления в сердечнике и оболочке. Другой тип ФКС для заключения в себе света использует эффект фотонных запрещенных зон (брэгговское отражение), создаваемый микрострук-турированной оболочкой, за счет этого свет может удерживаться и распространяться даже в сердечнике с более низким по отношению к оболочке показате- лем преломления, в том числе и в полом сердечнике. Фотонная запрещенная зона, возникающая в спектре пропускания (зависимость коэффициента пропускания от длины волны) двумерной периодической оболочки световода данного типа, обеспечивает высокий коэффициент отражения для излучения, распространяющегося вдоль полого сердечника, позволяя существенно снизить потери, присущие модам обычных полых световодов со сплошной оболочкой и быстро растущие [2] с уменьшением диаметра полого сердечника. Среди световодов второго типа выделяется несколько групп. Световоды с полым сердечником – центральное отверстие, как правило, большего радиуса, окружается «кольцами» микроотверстий. Волокно Брэгга [3-7] имеет полый сердечник, окруженный оболочкой, образованной чередующимися кольцами с низким и высоким показателями преломления. В работе [8] демонстрируется волокно Брэгга с заполненным материалом (твердым) сердечником, рабочая область которого может быть смещена в видимый диапазон путем варьирования толщины оболочки из брэгговских отражающих колец. Твердотельные световоды [9, 10], оболочка которых содержит стержни с высоким показателем преломления, размещенные в основном материале световода с низким показателем преломления. Кроме того, в обоих типах световодов может варьироваться целый ряд параметров (рис.1), таких как форма микроотверстий (круглые, квадратные, эллиптические) [11], схема локализации микроотверстий (правильные шестиугольная и прямоугольная решетки, неправильные решетки) [12, 13], количество сердечников [14, 15], количество дефектов, образующих сердечник [16, 17], материал, заполняющий микроотверстия [18, 19]. Так, например, в работе [20] полости в оболочке ФКС заполнялись жидкими кристаллами, что породило гибридный механизм распространения света: эффект полного внутреннего отражения и эффект фотонных запрещенных зон действуют соответственно на ортогонально поляризованные моды. О применении ФКС, заполненных жидкими кристаллами, в оптических свичах говорится в работах [21-23].

ill 000000000000 0000000000000 л0Д0Д0Д00Д0Д0Д0л

. W.

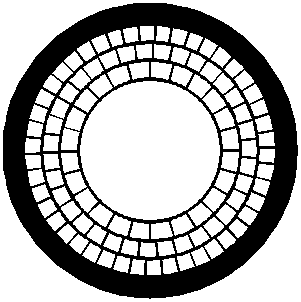
Рис. 1. Сечения различных типов ФКС: (а) - схема сплюснутой шестиугольной решетки с эллиптическими отверстиями [12], (б) - схема сечения волокна Брэгга с тремя концентрическими цилиндрическими слоями кварца [6], (в) - оптический микроснимок сечения твердотельного световода, светлые и темные области на снимке соответствуют областям с низким и высоким показателями преломления [10]

С созданием ФКС появились новые степени свободы для управления характеристиками световода, позволившие эффективно управлять дисперсией, делать волокна с очень высокой или очень низкой нелинейностью, с большой или малой эффективной площадью моды и т.д.

Теоретический интерес к ФКС вызван в большей степени фактом наличия в их структуре больших контрастов показателя преломления, чем в обычных слабонаправляющих волокнах, и, как следствие, необходимости создания специальных работоспособных методов их исследования. Стоит отметить, что способность ФКС заключать в себе свет зависит от множества факторов, таких как количество микровключений, их местоположение, соотношение диаметра и расстояния межд у центрами. Это дает широкое поле деятельности для проектирования световодов с заранее заданны ми свойствами .

С общей точки зрения, фотонный кристалл является сверхрешеткой (crystal superlattice) – средой, в которой искусственно создана периодическая модуляция какой-либо внутренней характеристики вещества, на порядки превышающая период основной атомной решетки вещества. Для фотонов такую модуляцию получают периодическим изменением коэффициента преломления среды в одном, двух или трех измерениях (1D-, 2D-, 3D-фотонные структуры соответственно). Если период оптической сверхрешетки сравним с длиной электромагнитной волны, то поведение фотонов кардинально отличается от их поведения в решетке обычного кристалла, узлы которого находятся друг от друга на расстоянии, много меньшем длины волны света. Поэтому такие решетки и получили особое название – фотонные кристаллы.

Понятие разрешенных и запрещ енных энергетических зон является основным в твердотельной электронике. В оптике твердого тела схожие понятия появились лишь в 1987 году [24]. Как и электрические среды, в зависимости от ширины запрещенных зон фотонные кристаллы можно разделить на проводники – вещества, способные проводить свет на большие расстояния с малым поглощением, диэлектрики – практически идеальные зеркала, полупроводники – вещества, способные, например, выборочно отражать фотоны определенной длины волны, и сверхпроводники, в которых благодаря коллективным явлениям фотоны распространяются практически на неограниченные расстояния.

Аналогично примесному атому, нарушающему трансляционную симметрию атомного потенциала, изменения диэлектрической проницаемости в определенной области фотонного кристалла нарушают трансляционную симметрию и приводят к появлению разрешенной моды внутри фотонной запрещенной зоны, локализованной в пространственной окрестности дефекта.

Изготавливаемые путем набора однородных стержней или трубок в заготовки и последующей вытяжки их в волокна, имеющие полости (неоднородности) по всей длине, ФКС по аналогии с кристаллами имеют зонную энергетическую структуру, т. е. у них существуют разрешенные и запрещенные энергетические зоны, в которых свет с определенной длиной волны либо может, либо не может распространяться вдоль волокна. Такой световод в поперечном сечении является двумерным кристаллом с зонной структурой фотонного изолятора. При этом в продольном направлении волокно является идеальным проводником.

Заготовки для производства ФКС могут выполняться из различных диэлектрических материалов, таких как кварц, полимеры, легкоплавкие ст екла. Кварц используется часто по причине прозрачности в широком диапазоне длин волн. Заготовки обычно имеют длину порядка 400-600 мм, внешний диаметр – 20-40 мм и содержат исходные элементы (стержни, труб ки), формирующие затем микроструктуру размерами порядка 0,5-5 мм [25]. Впоследствии заготовки вытягиваются в волокна диаметром около 100 мкм с конечными размерами элементов структуры порядка одного микрометра и меньше. В процессе вытягивания геометрия исходной микроструктуры может деформироваться, исследованию влия- ния ее искажения на дисперсию и свойство двулучепреломления посвящены работы [26, 27].

Благодаря оболочке в виде фотонного кристалла ФКС обладают рядом свойств, отличающих их от обычных световодов. Так, ФКС мог ут быть одномодовыми в очень широком диапазоне длин волн [28]. Величина и наклон кривой дисперсии групповой скорости может сильно меняться в зависимости от геометрических параметров ФКС, что позволяет, например, сместить ее нулевое значение в область более коротких длин волн, чем у стекла, получить дисперсию с малым наклоном в достаточно широком диапазоне длин волн или треб уемое значени е дисперсии на заданной длине волны [29-33]. В работе [34] исслед уется связь межд у эффективной площадью моды и дисперсией. ФКС, дисперсия которого может изменяться в широких пределах за счет незначительного изменения показателя преломления материала, производимого фоточувствительным германием, присутствующим в составе в качестве добавки, предложен в работе [35]. Обладающие аномальной дисперсией групповой скорости ФКС могут быть использованы в качестве компенсаторов дисперсии [36]. Анизотропия формы сечения ФКС, связанная, например, с использованием множественного дефекта для образования сердечника [17] или геометрически неправильных реш еток периодической структуры оболочки, приводит к возникновению двулучепреломления. Ортогонально поляризованные моды в таких световодах различаются постоянными распространения, т.е. проекциями на оптическую ось волнового вектора моды, эффективными модовыми индексами, групповыми скоростями, значениями дисперсии групповой скорости и другими параметрами. Структура ФКС позволяет достигать больших, порядка 10 ^-2 , значений параметра двулучепреломления 8 n = n efj - n f , где n f и n _e ^y _ff – эффективные модовые индексы ортогонально поляризованных мод [12]. ФКС со значительным двулучепреломлением привлекательны для использования в оптических сенсорах. В таких световодах удается осуществить преобразование частоты лазерных импульсов и поляризационное управление явлением генерации суперконтинуума – искусственного белого света, получаемого в результате нелинейно-оптического преобразования сверхкоротких лазерных импульсов [37].

Масштабное преобразование геометрии одномодового ФКС позволяет изменять эффективную площадь моды в широких пределах (практически на два порядка), что дает возможность управления величиной нелинейных эффектов в ФКС [31, 38]. ФКС с большой площадью моды позволяют достигать высоких энергий лазерны х импульсов в волоконных лазерах и усилит елях [15].

Оптические солитоны – важный класс объектов нелинейной оптики, используемых для передачи оптических сигналов на большие расстояния и позволяющих наблюдать новые нелинейно-оптические явления [39]. ФКС с полым сердечником позволяют сформировать устойчивые изолированные моды (солитоны) мощных сверхкоротких световых импульсов и осуществлять эффективные нелинейнооптические преобразования таких полей [40]. Полые ФКС открывают широкие возможности для передачи нано- и пикосекундных импульсов высокой мощности для биомедицинских и технологических приложений [41].

Для целей передачи информации наиболее важной задачей является создание световодов, в которых удаст ся снизить затухание до величины меньше фундаментального предела затухания обычных кварцевых световодов, порядка 0,2 дБ/км, определяемого рэлеевским рассеянием в материале волокна. Сердечники ФКС обычно изготавливаются из кварца, поэтому уменьшение затухания в них ниже фундаментального предела невозможно так же, как в обычных волокнах. Для ФКС, в основе действия которых лежит эффект фотонных запрещенных зон, в случае падения света с длиной волны, лежащей в запрещ енной зоне полубесконечной периодической структуры оболочки, должно происходить полное отражение падающего света, но так как в реальных световодах количество периодических слоев ограничено, происходит частичное вытекание света из волокна. В работе [42] показано, что данные потери можно сократить до уровня ниже 0,01 дБ/км. Оптимизации слоев оболочки брэгговских волокон с точки зрения минимизации потерь посвящена работа [43]. Установлено [44], что значительный вклад в потери ФКС с полым сердечником вносит механизм рассеяния, основанный на перекачке энергии направляемы х мод в поверхностные моды оболочки [45], которых нет в обычном кварцевом волокне, поэтому необходимо обеспечить отсутствие самих поверхностных мод [46, 47] или, как минимум, чтобы в спектральной области фотонных запрещенных зон отсутствовал волновой синхронизм межд у направляемыми и поверхностными модами. Для волокон Брэгга, как показано в работе [48], общие потери можно снизить до уровня от 0,01 до 0,1 дБ/км при использовании в оболочке материала с затуханием 10 дБ/км. Твердотельные световоды, обладающие лучшей устойчивостью к механическим воздействиям по сравнению с полыми световодами, демонстрируют большие потери при распространении света, составляющие порядка 2 дБ/км в случае использования вокруг каждого стержня дополнительного слоя с еще более низким показателем преломления, нежели основной материал оболочки [10].

В данной работе прив еден краткий обзор существующих методов расчета мод ФКС, а также проведено сравнение межд у н екоторыми из них. В работе показано, что значения эффективного индекса для фундаментальной моды, полученные с помощью КР-метода и коммерческой программы FIMMWAVE для двух моделей ФКС с заполненным сердечником совпадают с точностью до 0,2 %. По- казано также, что разработанная авторами реализация ССМ-метода в среде Matlab [80] дает более устойчивую и монотонную сходимость, а также существенно меньшую величину ошибки при малом числе локальных мод (до 20 мод), чем коммерческая программа FIMMWAVE.

Методы расчета мод фотонно-кристалли ческих световодов

Основной задачей исследования ФКС, как и световода любого другого типа, является проблема отыскания его мод – электромагнитных полей , способных в нем распространяться. Исторически первым методом, примененным для расчета мод ФКС, стал метод эффективного индекса [28, 49-51]. Метод эффективного индекса является одним из самых быстрых, суть его состоит в замене сложной модели сечения ФКС с множеством микроотверстий на адекватную модель обычного круглого световода со ступенчатым профилем показателя преломления. При этом метод уступает конкурентам по точности.

Существует несколько методов, предназначенных для расчета мод ФКС. Все их можно условно разделить на три группы: приближенно-аналитические методы, или методы декомпозиции, интегральные методы и конечно-разностные методы.

Методы декомпозиции

Основная идея, эксплуатируемая в данной группе методов, – это возможность представления поля моды световода в форме разложения по некоторому базису. В результате чего отыскание мод сводится к задаче на собственные значения и собственные вектора некоторой матрицы .

Разложение по плоским волнам [32] с периодическими граничными условиями дает решение для бесконечного, периодически повторяющегося в поперечной плоскости световода, что делает принципиально невозможным получение данны м методом мнимой части константы распространения, соответствующей потерям при распространении вытекающей или несобственной моды.

Метод разложения по модам Гаусса-Эрмита [29, 30] оказывается более пригодным для описания сложной структуры сечения ФКС, нежели метод разложения по плоским волнам, однако данный метод ограничен применени ем только к ФКС с отверстиями в оболочке, расположенными в узлах правильной гексагональной решетки, так как расстояние межд у центрами любых двух соседних отверстий должно быть фиксировано, и это значение входит в выражение для базисных ф ункц ий.

Обобщением метода мультиполя, применяемого обычно для световодов с несколькими сердечниками, на случай ФКС можно считать работу [52]. Ключевым аспектом предлагаемого авторами метода мультиполя является то, что он с выгодой использует факт округлости включений и свойства симметрии, присущие многим ФКС, в связи с рег у-лярностью расположения микроотверстий [53].

Сильная сторона метода также состоит в том, что он позволяет вычислять как действительную, так и мнимую части константы распространения. В отличие от подхода мультиполя для световодов с несколькими сердечниками, продемонстрированного в работе [54], использующего технику поточечной стыковки поля на границах включений, метод [52] обрабатывает граничные условия путем разложения компонент поля по ортонормальному базису. Авторы утверждают, что применение метода может быть расширено также на световоды с произвольной формой включений, в соответствии со стратегией , предложенной в работе [55].

Характерной чертой метода согласованных синусоидальных мод (ССМ-метод) [56] является техника разбиения неоднородного сечения волноводной структуры на прямо угольные области с постоянным значением показателя преломления среды. В каждой из таких област ей поле моды аппроксимируется суперпозицией факторизованных гармонических ф ункций . А константы распространения мод находятся из условия минимизации невязки представлений поля на границах соседних област ей, для чего используется интегральный подход. Метод согласованных синусоидальных мод использует процедуры поиска корней уравнений, и потому проигрывает по скорости методам, основанным исключительно на отыскании собственных чисел матриц.

Интегральные методы

Интегральные методы являются сеточными, то есть в отличие от методов предыдущей группы в данном случае решением задачи отыскания поля моды является сеточная функция, а не заданная аналитически.

Среди этой группы можно выделить метод конечных элементов [57, 58]. Он представляет собой мощный инструмент векторного анализа, способный учитывать все особенности геометрии микроотверстий и расположени е их в структуре сечения. Достаточно быстрый и гибкий, он часто используется для моделирования свойств ФКС. Среди недостатков метода конечных элементов можно назвать требовательность к ресурсам памяти, так как для описания структуры сечения ФКС треб уется подробная дискретизация и большое количество переменных, а также необходимость вмешательства человека в работу алгоритма для лучшего определения граничных условий (Perfectly matched layer) и сетки дискретизации.

Метод граничных элементов [59], где сечение разбивается на однородные области, а задача на собственные значения получается в результате применения теоремы Грина, отличает меньшая требовательность к ресурсам памяти. Однако существенным недостатком является возможность возникновения ложных решений .

В методе функции Грина [60] задача отыскания констант распространения мод также сводится к задаче на собственные числа матрицы , для решения которой разработан специальный быстрый алгоритм. Этот метод работоспособен в случае сложны х геометрических форм микроотверстий, хотя и с меньшей скоростью сходимости, чем в случае круглых отверстий.

Конечно-разностные методы

Конечно-разностные методы так же, как и методы интегральные, дают сеточное решение.

Метод конечных разностей (КР-метод) широко используется для решения разного рода уравнений . Благодаря простоте реализации этот метод стал удобным инструментом для расчета мод оптических световодов, особенно тех, для которых не существует аналитического решения, например, таких как ФКС. Наличие больших контрастов показателя преломления в структуре сечения ФКС треб ует использования полностью векторного подхода при расчете мод вместо часто используемого для слабонаправляющих световодов скалярного подхода. Однако, как было продемонстрировано в работе [61], скалярный конечно-разностный метод может использоваться для получения как минимум качественной оценки распределения мод ФКС, в том числе на основе эффекта фотонных запрещенных зон.

Для более точного анализа были предложены векторные конечно-разностные схемы [62]. Дискретизации подвергаются дифференциальные операторы и ф ун кции, входящие в уравнение Гельмгольца или волновые уравнения. В работе [63] представлен конечно-разностный пространственно-временной подход (FDTD-метод) расчета мод ФКС с использованием сдвинутых сеток (ячеек Йи). Усовершенствованному конечно-разностному пространственновременному метод у, учитывающему дисперсию материала, посвящена публикация [64].

Результатом применения специальных конечно-разностных схем к нестационарным волновым уравнениям или уравнениям Максвелла является семейство методов распространения пучка [6567]. Суть методов состоит в моделировании распространения когерентного пучка света вдо ль св етовод а, в результате чего по лучаю т моды данной структуры как бы апостериорно . С помо щью метода удобно исследовать энергетич еские по тери при про хожд ении излуч ения по св етоводу, хо -тя это мо жет быть и затруднительно в связи с проб лемо й сходимости метод а к усто йчивому состоя нию , а пло хо сходящиеся резуль таты для многомодового световод а будут по лучаться всякий раз, когд а более одно й моды достиг аю т устойчивого состояния одновременно.

Модернизация ССМ-метода

Базовая идея ССМ-метода, близкая к идее другого метода - метода поперечного резонанса [68, 69], была впервые сформулирована в работе [70]. Последующее развитие метод получил в работе [71], где его применяли для расчета потерь излучения за счет вытекающих мод в ступенчатых световодах. Затем в работах [56, 72] был введен описательный термин

«согласование синусоидальных мод» и дана точная математическая формулировка. Близость метода поперечного резонанса и другого широко используемого метода – метода линий [73, 74], отмечалась уже неоднократно [75, 76]. Подход бинаправленного распространения собственной моды [77] и метод бинаправленного распространения, основанный на методе линий [78], позволяют вычислять распределение любых (не только модовых) полей в оптических св етоводах. Оба они могут рассматриваться как частные случаи метода поперечного резонанса. Несмотря на преимущества данного подхода, связанные с возможностями полного векторного анализа и непрерывным характером результирующего поля, ССМ-метод до публикации авторов [79] не применялся для моделирования ФКС. Кроме того, в ССМ-методе процедуры поиска корней (нулей ф ункци и) как на начальном этапе отыскания локальных мод, так и при определении константы распространения обладают существенным недостатком, а именно: возможен пропуск корней в том случае, если они располагаются вблизи друг друг а или вблизи разрыва функции на расстоянии меньше шага дискретизации. Пропуск корней в первом случае ведет к неверному реш ению для пространственной моды, а во втором – и вовсе к ошибочному отрицанию факта существования моды световода с некоторым значением константы распространения. Поэтому в работе [80] ССМ-метод был модифицирован на этапе отыскания констант распространения с помощью итеративного метода Крылова решения нелинейной матричной задачи на собственные значения и вектора. А на этапе поиска локальных мод авторами предложен оригинальный «статистический» алгоритм нахождения нулей непрерывной ф унк ции.

Модернизация КР-метода

За основу конечно-разностного метода, рассматриваемого в настоящей работе, был взят подход, предложенный в работе [11], где для расчета мод использовалась техника применения конечноразностных ап проксимаций к стационарным векторным волновым уравнениям для монохроматического света. КР-метод выигрывает (в несколько раз) по скорости работы алгоритма у СС М-метода, поскольку задача отыскания константы распространения и отсчетов сеточных решений для поперечных компонент электрической или магнитной составляющих напрямую сводится к линейной матричной задаче на собственные числа и вектора. В работе [11] приводится вывод только для электрической составляющей электромагнитного поля. Компоненты магнитной составляющей могут быть рассчитаны через компоненты электрической составляющей путем численного их дифференцирования, что влечет возникновение дополнительных ошибок. В работе [81] формулируется математическая задача расчета магнитной составляющей светового поля и строится алгоритм ее решения. Полностью расписана структура матрицы линейной задачи на собст- венные значения и в ектора для электрической составляющей, которая не показана в [11]. Совместное решение двух аналогичных, но независимых задач для электрической и магнитной составляющих электромагнитного поля позволяет произвести контроль правильности работы метода путем сравнения значений констант распространения.

Сравнение реализаций ССМ- и КР-метода с программой FIMMWAVE

Для модели ФКС, сечение которого изображено на рис.2, и длины волны λ = 1,3 мкм в FIMMWAVE с применением FMM Solver (real) с числом локальных y -мод равным шестидесяти была получена фундаментальная мода с эффективным индексом 1,4477.

Полученны е авторами ранее [82] результаты с помощью реализаций модернизированных ССМ- и КР-методов для данной модели сравниваются с результатом работы FIMMWAVE в Таблиц е 1.

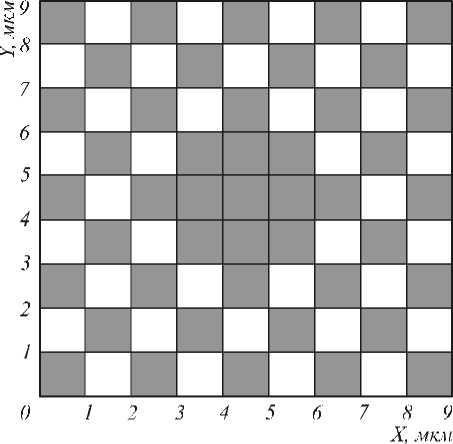
Рис. 2. Модель сечения фотонно-кристаллического световода: темным показаны области со значением показателя преломления п 1 =1,47, светлым - с п 2 = 1

Таблица 1. Абсолютное и относительное отклонения значений эффективного индекса фундаментальной моды ФКС (рис. 2.), рассчитанных разными методами, от результата, полученного FIMMWAVE

Метод	Эффективный индекс, n eff	Абсолютное отклонение, А	Относительное отклонение, 8
КР-метод, п х х n y =52 x 52	1,4480	0,0003	0,02%
ССМ-метод (векторный)	1,4473	0,0004	0,03%
ССМ-метод (скалярный)	1,4491	0,0014	0,10%
FMM Solver (real)	1,4477	0	0

Как след ует из Таблицы 1, результаты трех рассмотренных методов отличаются от результата FMM Solver (real) не более чем на одну десятую процента. На рис.3 показаны распределения интенсивности моды, рассчитанной программой FIMMWAVE (г), скалярной моды, полученной ССМ-методом (а), и основной векторной компоненты магнитного поля, полученной ССМ-методом (б) и КР-методом (в). Из рис. 3 видно, что все четыре картины основной моды очень близки.

Для другой модели ФКС (рис. 4) с круглыми отверстиями и заполненным сердечником, расчет фундаментальной моды которого в работе [83] производился с помощью только КР-метода, также было проведено сравнение с коммерческой программой FIMMWAVE.

При прочих равных параметрах модели и количестве локальных y-мод FMM Solver (real) равном тридцати было получено значение эффективного индекса n efflMMWAVE = 1,4533. Таким образом, относительное отклонение значения, полученного КР-методом n f = 1,4509, составляет 0,17 %.

На рис.4 по казаны два аналогичных сечения ФКС, но ря дов отв ерстий в мод ели на рис.4б на один меньше, чем на рис.4а. Это сд елано для того, чтобы показать, что увеличение числа рядо в отв ерстий в о бо лоч ке ФКС больше трех не приводит к заметному влиянию на параметры о снов -ной моды.

На рис.5 показаны распределения модулей амплитуд поперечных электрических составляющих фундаментальной моды, рассчитанных для ФКС (рис.4) КР-методом (а, б) и программой FIMMWAVE (в, г). Из рис. 5 видно, что оба метода дают почти одинаковые картины фундаментальной моды, и что эта мода почти вся сосредоточена в сердечнике ФКС.

В сопровождающей документации к программному продукту FIMMWAVE рекомендовано использовать минимальное число локальных мод, равное тридцати, что согласуется с исследованиями сходимости метода, проведенными в [79]. Сравним две реализации СММ-метода: предложенную в работе [80] и коммерческую программу FIMMWAVE – на сходимость относительно числа локальных мод. Изменение относительной ошибки расчета одного из выходных параметров – константы распространения, от числа локальных мод в диапазоне от 10 до 60 для ФКС (рис. 2) показано на рис. 6.

Из сравнения графиков на рис.6 следует, что предложенная в работе [80] реализация в среде Matlab 7.0 дает более устойчивую и монотонную сходимость, а также существенно меньшую величину ошибки при малом числе локальных мод (до 20), чем коммерческая программа FIMMWAVE. Если выбрать число локальных мод при расчете ССМ-методом больше 30, но меньше 60, то обе реализации будут давать практически одинаковые результаты (рис. 6).

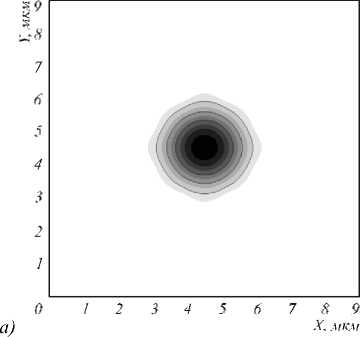
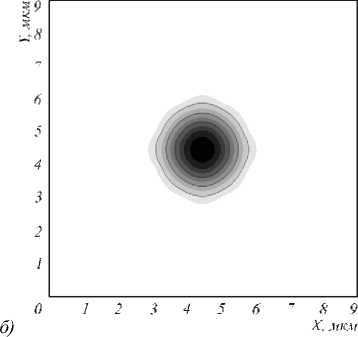
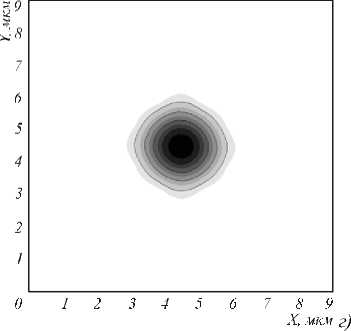
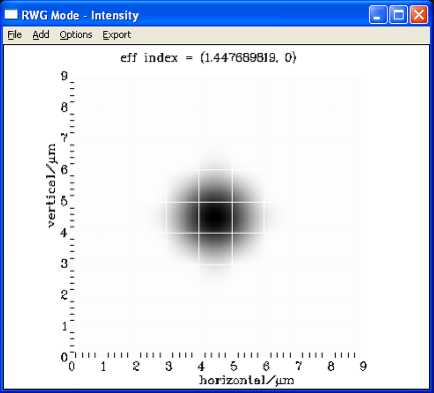
Рис 3. Для модели ФКС (рис. 2) распределения квадрата модуля амплитуды скалярного поля фундаментальной моды, рассчитанное ССМ-методом (а), распределения квадрата модуля амплитуды наибольшей векторной компоненты Hy фундаментальной моды , рассчитанное ССМ- методом ( б), распределения квадрата модуля амплитуды наибольшей векторной компоненты Hy фундаментальной моды, рассчитанное КР-методом (в), и распределения интенсивности фундаментальной моды, полученное в программе FIMMWAVE (г)

-4 -3 -2 -10  12  3  4

а)                                     ^Л б)

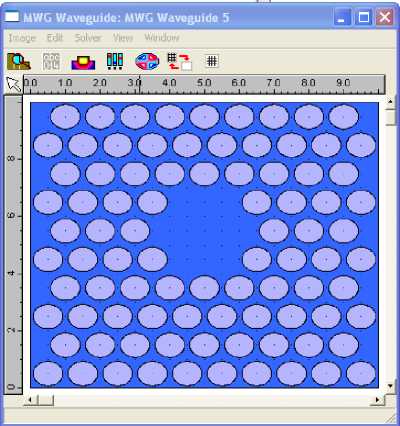
Рис. 4. Модель сечения ФКС (а): темным показаны области со значением показателя преломления n 1 = 1,46 , светлым – отверстия, заполненные воздухом n 2 = 1 ; окно программы FIMMWAVE с моделью сечения аналогичного световода (б), но количество рядов отверстий по вертикали на один меньше

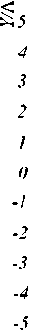
-4 -3 -2 -10  12 3 4

а)                                  АЛ

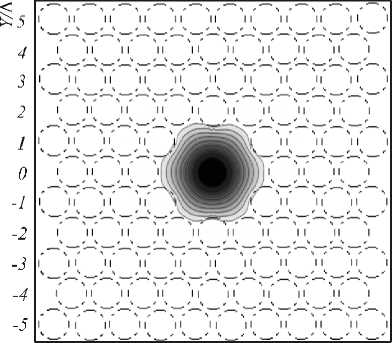
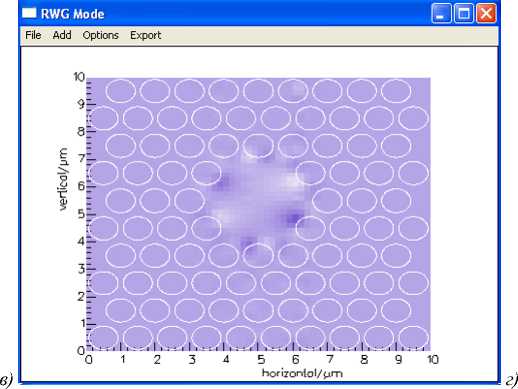
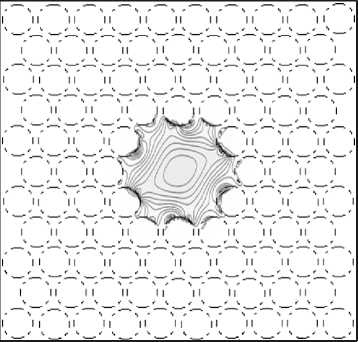
Рис. 5. Для модели ФКС (рис. 4а) распределения абсолютных значений амплитуды поперечных электрических составляющих фундаментальной моды: E_x (а) и E_y (б), рассчитанные КР-методом, и для модели ФКС (рис.4б) – E_x (в)

-4 -з _2 -10  12  3 4

б)                                  XX

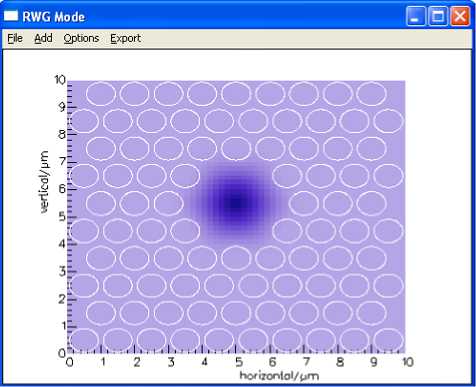
и E_y (г) , полученные программой FIMMWAVE

22 0,0012

J 0,0010

§ 0,0008

I 0,0006

| 0,0004

~ 0,0002

-0,0002

		---CCM Matlab ..........CCM KMMW'AVK
	*'•,-♦,

0   10   20   30   40   50 К

Рис. 6. Зависимость относительной ошибки константы распространения фундаментальной моды ФКС (рис. 2) от числа локальных мод для двух реализаций ССМ-метода

Заключение

В работе дан обзор методов расчета мод фотонно-кристаллических световодов и получены следующие результаты:

• 1.    Значения эффективного индекса для фундаментальной моды, полученные с помощью КР-метода и коммерческой программы FIMMWAVE для двух моделей ФКС с заполненны м сердечником совпадают с точностью до 0,2% .

• 2.    Разработанная авторами реализация ССМ-метода в среде Matlab [80] дает более устойчивую и монотонную сходимость, а также существенно меньшую величину ошибки при малом числе локальных мод, чем коммерческая программа FIMMWAVE.

Работа выполнена при финансовой поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF PG08-014-1), гранта РФФИ 08-0799007 и гранта Президента РФ поддержки вед ущи х научных школ (НШ-3086.2008.9).