Расчет мод полого фотонно-кристаллического световода разностным методом

Все большую популярность, благодаря своим нетривиальным свойствам, в наши дни приобретают микроструктурированные волокна или фотонно-кристаллические световоды (ФКС). Это относительно новый класс оптических волокон, обладающих свойствами фотонных кристаллов [1]. В настоящий момент ФКС находят применение в сфере коммуникаций, волоконных лазерах, устройствах нелинейной оптики, оптических линиях передачи излучения высокой мощности, высокочувствительных газовых сенсорах. Известно два основных типа ФКС, представляющих практический и теоретический интерес: волокна со сплошным сердечником, окруженным несколькими рядами микроотверстий, обычно располагающихся в форме шестиугольника [2, 3], и волокна с полым сердечником – центральное отверстие, как правило, большего радиуса, также окружается “кольцами” микроотверстий [4]. Такое волокно в поперечном сечении является двумерным кристаллом с зонной структурой фотонного изолятора. При этом в продольном направлении волокно является идеальным проводником света. Теоретический интерес к ФКС вызван в большей степени фактом наличия в их структуре больших контрастов показателя преломления, чем в обычных сла-бонаправляюших волноводах, и как следствие необходимости создания специальных работоспособных методов их исследования.

Стоит отметить, что способность ФКС заключать в себе свет, зависит от множества факторов, таких как количество микровключений, их местоположение и форма [5, 6], соотношение диаметра микроотверстий и расстояния между центрами ближайших микроотверстий, что дает широкое поле деятельности для моделирования их свойств [7].

В данной работе на основе разностного решения векторного волнового уравнения для монохроматического электромагнитного излучения, которое сведено к решению линейной задачи на собственные вектора и собственные значения, рассчитаны распределения поперечных составляющих электрического вектора (вектора напряженности электрического поля) для основной моды полого ФКС. Численно получена почти линейная зависимость эффективного показателя преломления этой моды от длины волны (в видимом диапазоне), а также показано, что дисперсионный параметр для ФКС с полым сердечником положительный и в два раза меньше по абсолютной величине, чем для такого же ФКС с заполненным сердечником.

Конечно-разностный метод решения волновых уравнений

За основу был взят подход, предложенный в работе [6], который ранее был применен нами к круглым волокнам [8]. В [6] для расчета мод использовался метод конечноразностного решения векторных волновых уравнений для монохроматического света.

Рассмотрим однородные волновые уравнения для монохроматического излучения в диэлектрической среде без источников [6,9]:

V ² E + v ( v ln n ² • e ) + k ₀ ² n ² E = 0; (1)

PE yx

A '(Ex Inn2)   d2Ex dy [    dx    J  dydx , (8)

Q„H,    H + (1 + ln n ²) ^-H T -— (In n² — ) + n²k 0 H (9)

" ^x     d x ²                 d y ²     d y        d y         ^{0 x ,(} )

V ² H - ( Vx H ) xV ln n ² + n ² k 0 H = 0, (2)

где n – показатель преломления среды, зависящий от поперечных координат (x,y), k ₀ = 2 п / X - волновое число в вакууме, х -длина волны света.

Далее применим уравнения (1) и (2) для волноводов, однородных вдоль продольной оси z. При этом электрическая и магнитная

Q yy H y

Q

, d² h,   d² h,    a ,5 h,     , ,

(1 + ln n ²)--- ^- +-- (ln n^г--- y ) + n^гk 2 H , (10)

d x ²      d y ²     d y        d y        ⁰ y ^{,( V)}

xy H y

d d H H,        , d ² H,

= —(In n ²----) - In n ²----- (11)

d y        d x            d y d x , ⁽ )

составляющие поля можно представить в виде E ( x , y , z ) = E ( x , y )exp( - ik z z ) и H ( x , y , z ) = H ( x , y )exp( - ik z z ), где E ( x , y ) и H ( x , y ) - напряженности электрической и магнитной составляющих электромагнитно-

Q yx H x

9_n dHH_xx ,   ₂d² H_x

= —^(ln n -x- ) ^- ln n —-x- . (12) d x        d y          d x d y

го поля в поперечной плоскости, k_z – константа распространения. Далее используются граничные условия Неймана d E = о и d H = о , где n - вектор нормали к границам исследуемой области. Принимая во внимание

Заменяя непрерывные дифференциальные операторы конечно-разностными и используя следующие аппроксимации:

^d f ⁽ x , y ) 8x

^d f ⁽ x , y )

xi

f ⁽ x i + 1 , y ) ^- f ⁽ x i - 1 , y )

2 h x

,

f ⁽ x , y j + 1 ) ^- f ⁽ x , y j - 1 )

инвариантность волновода вдоль продольной d ।     2

справедливость равенств nn = о, и H                            5 z d z

оси z и

а e d z

- ik _z E

5 y

y j

2 h y

, (14)

(1) и (2) форме:

можно

ik z H , векторные уравнения представить в матричной

^{d 2} f ⁽ x , y ) d x²

xi

f ⁽ x i - 1 , y ) ^{- 2} f ⁽ x i , y ) ⁺ f ⁽ x i + 1 , y )

h x ²

,(15)

P xx	p 1 xy P yy J	Г E^ "  x	= k z	Г Ex "  x
Pyx		L E y j		L E y j	,     (3)

Q xx	Q xy "	" H x "	= k z	Г H x ~
Q yx	Q yy J	_ H y J		. H, j	,     (4)

8 ² f ( x , y )        f ^{( x} , y j - 1 ) ^{- 2} f ^{( x} , y j ) ⁺ f ^{( x} , y j + 1 )

^y^ ⁼----------h 2 ----------,(16)

y j                                            y

где непрерывные дифференциальные операторы P_ij и Q_ij определяются следующим образом:

^d f ^{( x} , y ) I d x d y |

[ f ^{( x} , + 1 , y j + i ) - f ^{( x} , + 1 , y j - i )] - ^[ f ^{( x} , - 1 , y j + i ) - f ^{( x} , - 1 , y j - ! ^)] 4 h_xh_y

,(17)

PE xx x

A d ( E x In n ²) d x      d x

5 ² E 7,7

^{+      + n k} 0 Ex ,(5)

оy              v 7

PE yy y

9 ² E y + ^_ 9 ( E y ln n ²)

d x ²    9 y       9 y

PE xy y

d   d ( E y In n ²)

5 x     5 y

⁺ n ^k 0 ^Ey ,(6)

9 ² E y d x d y ,

получаем две независимые задачи на собственные значения относительно квадрата константы распространения:

RE = k z E , (18)

SH = k z H . (19)

Размерность каждой из задач (18) и (19) 2 M x 2 M , где M = ⁿxⁿy , здесь - количество узлов сетки по соответствующим осям.

Матрицы задач (18) и (19) имеют сходную структуру, поэтому рассмотрим только матрицу R задачи (18). Она имеет следующий вид:

"  ~1 B12 O O O Anx +1 B nx + 2 O O O C11 A12 B13 Г nx +1 C2 Anx + 2 Rnx +3 B2 O C12 A13 O O O C22 A nx+3 O O O O C13 •.       Bnx-1 O O O nx + 3 C2 R 2 nx-1 B2 O Anx—1 B1nx A 2 nx-1 2nx B2 R = O O O Cnx-1 A~1nx O O O Г 2 nx-1 C2 A~22nx A~31 B32 O O O ~ nx +1 A4 Rnx + 2 B4 O O O C31 O B33 Г nx +1 C4 A nx + 2 A4 Rnx +3 B4 ,    (20) O C32 O O O O nx + 2 C4 Л nx +3 A4 O O O O C33 Д nx' B 3 O O O Cnx + 3 C4 R 2 nx-1 B4 O O B3nx A 2 nx-1 A4 2nx B4 . O O O Г nx1 C3 A~3nx O O O ,. 2 nx-1 C4 ~2nx A 4 где O - нулевая матрица размера nx х nx. Точные формулы для расчета ненулевых элементов матрицы (20) не приводятся ввиду громоздкости.

Вектор-столбцы E и H , являются собственными векторами в задачах (18) и (19) и содержат отсчеты всех четырех поперечных компонент моды.

Рассмотрим подробнее структуру вектора

E = ( E x , E y ) T , здесь Т – значок транспонирования и

Г E x = ( E E 2 E 3 ... Em ),

(22) ...       2 M ).

E y = ⁽ E M + 1   E M + 2   E M + 3

Таким образом, этот вектор содержит все отсчеты обеих результирующих компонент E_x и E_y . Аналогичным образом вектор H содержит отсчеты компонент H_x и H_y .

Расчет мод полого фотонно-кристаллического световода

В качестве объекта исследования была выбрана модель полого ФКС, сечение которо- го изображено на рис. 1(а). Темным на рисунке показан материал с показателем преломления n = 1,46, светлым областям на рисунке 1(а) соответствуют отверстия заполненные воздухом n = 1. Центральное отверстие является полым сердечником. Расстояние между центрами отверстий Л и длина волны X были выбраны таким образом, что их отношение X /Л равнялось 0,6. Коэффициент заполнения, равный отношению диаметра отверстия d к расстоянию между центрами соседних отверстий Л, составлял 0,85. Расчет проводился по всей области сечения, где была определена равномерная сетка размером 204x228, что позволило добиться точности построения результирующих компонент электромагнитного поля моды порядка 0,03Л. Поперечные электрические составляющие основной моды, полученные в результате решения задачи (18), изображены на рис. 1(б). Доля интенсивности каждой из компонент, сконцентрированной в сердечнике, составила 40% и 60%, для Ex и Ey соответственно.

График зависимости эффективного ин-

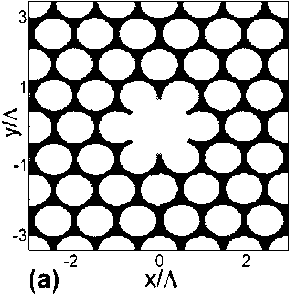
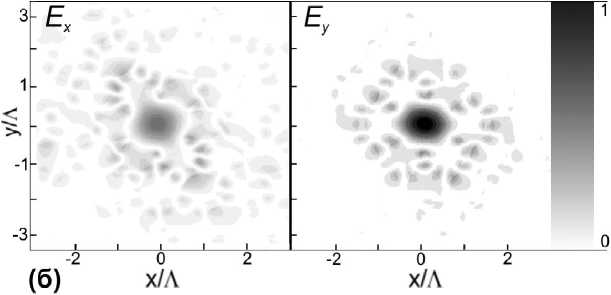
Рис. 1. (а) – сечение полого фотонно-кристаллического волновода, (б) – распределение абсолютных значений электрических составляющих основной моды Ex и Ey

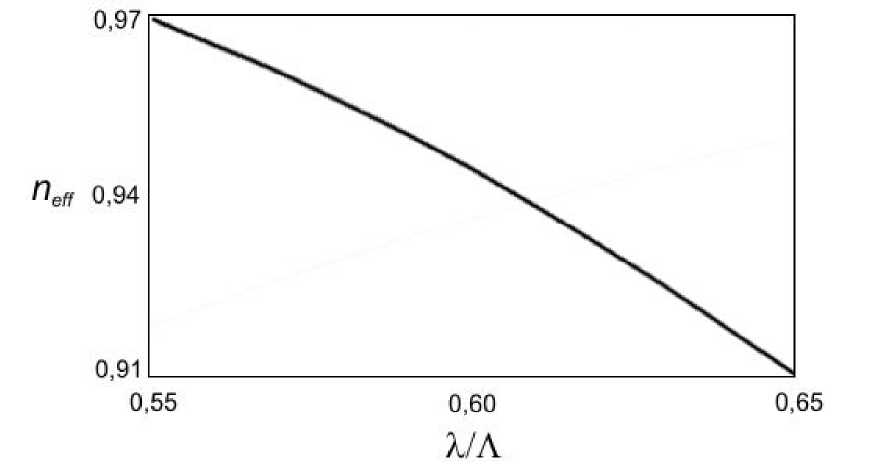
Рис. 2. График эффективного индекса основной моды для модели волновода, рассматриваемой в тексте

kz декса neff = k основной моды от соотношения λ /Λ пока0зан на рис. 2.

Из рис. 2 видно, что эффективный показатель преломления почти линейно убывает с ростом длины волны. Это означает, что дисперсионный параметр D , пропорциональный второй производной функции эффективного показателя преломления от длины волны D = - ( λ / c )( d ² n_eff / d λ ²), близок к нулю (рис. 3). В ФКС с заполненным сердечником зависимость дисперсионного коэффициента от длины волны обычно линейная и не нулевая [10, 11].

На рис. 3 для сравнения приведены две кривые дисперсионного параметра для ФКС с полым (сплошная линия) и заполненным (пунктирная линия) сердечниками (остальные параметры световодов одинаковые). Из рис.3 видно, что дисперсионный параметр для ФКС с полым сердечником положительный и убывает с ростом длины волны, а дисперсионный параметр для ФКС с заполненным сердечником – отрицательный, в два раза больше по абсолютной величине и также убывает по модулю с ростом длины волны излучения.

Таким образом, использование микро-структурированного волновода с полым сер-

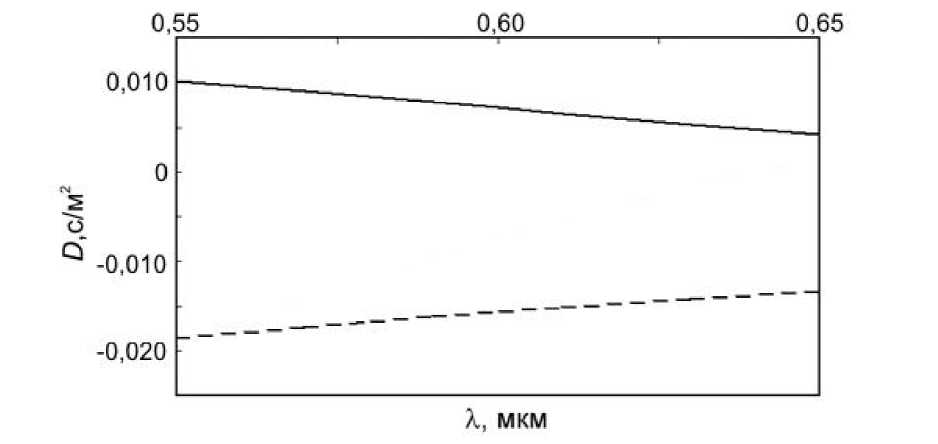
Рис. 3. График дисперсионного параметра для модели волновода, рассматриваемой в тексте - сплошная линия, для аналогичной модели с заполненным сердечником – пунктирная линия

Таблица 1. Доля энергии основной моды внутри сердечника для ФКС на рис. 1, приходящаяся на x и y составляющие электрического вектора

Коэффициент заполнения, d/Λ 0,79 0,85 0,91 Ex , % 15 40 8,7 Ey , % 40 60 20 дечником (по сравнению с таким же волноводом, но с заполненным сердечником) позволяет снизить хроматическую дисперсию в два раза.

Чтобы добиться нулевого дисперсионного коэффициента в некотором диапазоне длин волн, требуется увеличить долю энергии основной моды, распространяющуюся внутри полого сердечника. Однако это возможно не при любых параметрах ФКС. Например, в рассмотренном выше случае, увеличение и уменьшение размеров отверстий d приводит только к уменьшению энергии моды внутри сердечника. В табл. 1 показано, что только часть полной энергии основной моды, распространяющейся в ФКС на рисунке 1, сосредоточена внутри полого сердечника. Причем эта доля энергии зависит от коэффициента заполнения. Имеется некоторый оптимальный коэффициент заполнения (в нашем примере – 0,85), при котором максимальная доля энергии основной моды (в нашем случае -50%) сосредоточена внутри полого сердечника.

Заключение

В работе получены следующие результаты: 1) на основе волнового уравнения для электрического вектора монохроматической электромагнитной волны, записанного в разностной форме, сформулирована линейная задача на собственные вектора и значения, с помощью которой рассчитаны декартовы компоненты основной электрической моды фотонно-кристаллического волновода с полым сердечником; 2) численно показано, что дисперсионный параметр такого ФКС положительный, в отличие от дисперсионного параметра для ФКС с заполненным сердечником, и в два раза меньше по абсолютной величине; 3) численно показано, что для ФКС с полым сердечником имеется оптимальный коэффициент заполнения, при котором максимальная доля энергии основной моды (50%) распространяется внутри полого сердечника.

Работа выполнена при финансовой поддержке Российско-Американской программы “Фундаментальные исследования и высшее образование” (грант CRDF RUXO-014-SA-06) и гранта РФФИ 05-08-50298.