РАСЧЕТ МОДЕЛИ ЭТАЛОННОЙ УСТАНОВКИ ДЛЯ СОЗДАНИЯ ПОЛЯ МЕХАНИЧЕСКИХ НАПРЯЖЕНИЙ

ВВЕДЕНИЕ                   в определении абсолютных величин всех компо-

В настоящее время в промышленности и технике экспериментальное определение механических напряжений относится к области, которая называется "неразрушающий контроль" [1]. "Контроль" является скорее качественной, чем количественной характеристикой. Сейчас с помощью приборов неразрушающего контроля можно определить области в промышленных объектах, в которых напряжения повышены — зоны концентрации напряжений. Но современная промышленность настоятельно требует именно "измерений" — определения величин механических напряжений в абсолютных единицах мегапаскалях (МПа) с достоверным определением погрешности.

Механическое напряжение является аналогом давления в твердом теле. Давление давно практически измеримо — есть огромное число манометров, эталоны, воспроизводящие единицу давления в разных диапазонах, ГОСТ. Но это все — для жидкостей и газов. А для твердого тела всего этого нет — есть только несколько приборов неразрушающего контроля, которые могут быть применены для регистрации механических напряжений. И в настоящее время основная проблема состоит в том, что для измерения напряжений нет необходимой метрологической инфраструктуры — эталонной установки, наборов стандартных образцов, ГОСТов.

Механическое напряжение — это тензорнозначное поле σik (x). Симметричный тензор второго ранга σik имеет 6 независимых компонент [2], x — трехмерный вектор координат точек твердого тела. Задача измерения механических напряжений, как это необходимо для промышленности, состоит нент тензора напряжений в МПа в объекте контроля.

ПОДХОДЫ К ПРОБЛЕМЕ ИЗМЕРЕНИЙ МЕХАНИЧЕСКИХ НАПРЯЖЕНИЙ

Во ВНИИМ им. Д.И. Менделеева в течение ряда лет, начиная с 2009 г. [3], проводились экспериментальные работы по калибровке приборов неразрушающего контроля на металлических образцах, предоставляемых различными российскими промышленными предприятиями. Образцы располагались в силовой машине, входящей в комплекс установок Государственного первичного эталона единицы силы, на которой воспроизводится сила в диапазоне до 2 меганьютонов (Мн). Образцы имели форму плоских пластин, в центральной области которых создавалось одноосное по оси x постоянное напряжение

σxx(x)=σxx =σ = FS , где F — заданная сила, S — площадь прямоугольного поперечного сечения образца, остальные компоненты тензора напряжений равны нулю. Датчик прибора прижимался к поверхности образца в его центральной части, прибор измерял некоторую величину f.

Для ультразвукового прибора ИН-5101А [4, 5] сигнал f — это время в микросекундах (мкс) прихода отраженных от противоположной стороны пластины ультразвуковых импульсов трех разных поляризаций — двух поперечных и одной продольной. Из приведенных на рис. 1 данных видна линейная зависимость между сигналом прибора

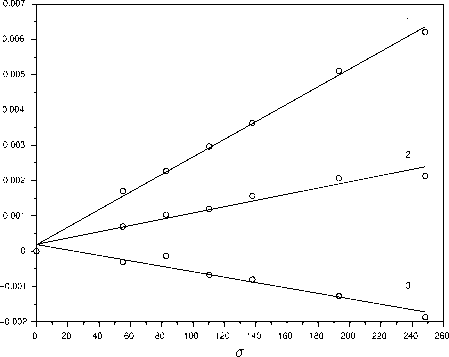
Рис. 1. Зависимость показаний f прибора ИН-5101А в мкс от напряжения σ [МПа].

Прямая 1 соответствует ультразвуковым волнам с поперечной поляризацией вдоль главной оси напряжений, 2 — поперечная поляризация с ориентацией перпендикулярно главной оси, 3 — волны с продольной поляризацией и напряжением. Здесь и на последующих графиках представленные экспериментальные данные обрабатывались методом линейной регрессии после вычитания показаний прибора f(0) при нулевом заданном напряжении.

Принцип действия прибора "Интроскан" осно-н на зависимости интенсивности шума Баркгау-на от механического напряжения в магнитных атериалах [6]. Экспериментальные данные зави-мости ( f — интенсивность шума Баркгаузена) учше аппроксимируются кубическим полиномом, ис. 2. Нелинейная зависимость характерна для агнитных явлений.

Показания прибора "StressVision" связаны с ве-ичиной магнитной анизотропии, возникающей од действием механического напряжения. При-денные на графиках рис. 3 экспериментальные чки соответствуют средней величине сигнала f о измерениям в 9 точках в центральной части об-азца. При параллельной ориентации датчика раз-ос экспериментальных точек для данного материала образца достаточно велик, поэтому построена линейная регрессионная зависимость. Для поперечной ориентации датчика точки лучше аппроксимируются кубической кривой. Прибор может настраиваться на толстый слой образца — 6 мм или на тонкий слой — 3 мм от поверхности. Это влияет, насколько глубоко в образец проникает зондирующий импульс и, соответственно, из какой области идет ответный сигнал, несущий информацию о напряжении. Сигнал с тонкого слоя, приповерхностного, сильно зависит от свойств поверхности металла, возможно подвергнутой фрезерной или токарной обработке, и поэтому имеющей значительные остаточные напряжения.

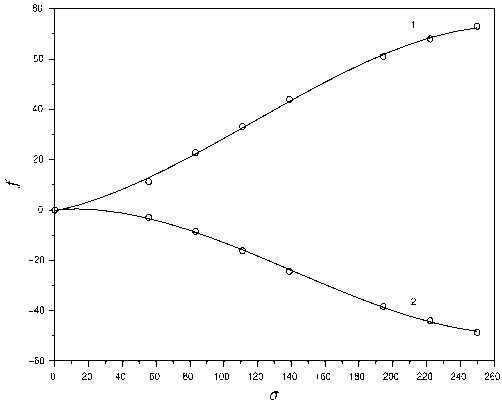
Рис. 2. Зависимость интенсивности шума Баркгаузена f , регистрируемого прибором "Интроскан", от напряжения σ [МПа].

Кривая 1 — ориентация датчика прибора вдоль главной оси напряжений, 2 — ориентация датчика поперек

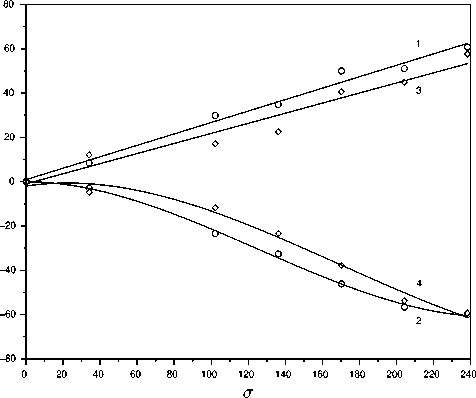
Рис. 3. Зависимость показаний прибора "StressVision" f в условных единицах от напряжения σ [МПа].

Прямые 1, 3 — ориентация датчика по направлению главной оси напряжения; кривые 2, 4 — ориентация датчика перпендикулярна направлению главной оси напряжения; 1, 2 — настройка прибора на тонкий слой; 3, 4 — настройка прибора на толстый слой

Из анализа полученных в многочисленных экспериментах данных (графики на рис. 1–3 приведены лишь как типичные иллюстрации) следует, что показания приборов существенным образом зависят от материала: химического состава и марки стали, от обработки поверхности (фрезерная, токарная), от технологии создания образца (прокат, ковка, закалка) и, возможно, других параметров. Для одноосного напряжения в образцах, на которых проводились эксперименты, наблюдается сильная зависимость показаний приборов от ориентации датчика относительно главной оси напряжений.

Задача калибровки приборов — это построение калибровочных кривых σ ( f ). Соответственно, кривые, показанные на рис. 1–3, необходимо обратить. Эта операция неоднозначная. Оказывается, что в ряде случаев даже знак неопределен, т.е. сжатие неотличимо от растяжения. Так, нижние кривые на рис. 3 отвечают растяжению при ориентации датчика перпендикулярно главной оси напряжений. И аналогичные кривые возникают при ориентации датчика параллельно главной оси, но при сжатии образца.

Калибровка прибора в лаборатории, эксперименты в лаборатории — это не самоцель. Задача состоит в измерении напряжений на промышленных объектах. А в реальных промышленных объектах априорно неизвестно, как направлена главная ось напряжений. И, соответственно, как следует ориентировать датчик прибора. А при разных ориентациях датчика получаются разные показания и, как было отмечено выше, даже разного знака.

Более того, нет никаких гарантий, что в исследуемом промышленном объекте напряжение будет одноосным. В общем случае у тензора напряжений есть 6 независимых компонент, при этом на поверхности — три независимые компоненты. Поэтому, если прибор откалиброван в лаборатории на одноосном напряжении, а в реальном промышленном объекте напряжение двухосное, то как интерпретировать показания прибора, непонятно.

В реальных объектах зависимость напряжения от пространственных координат x может быть достаточно сильной. При изгибе пластины или в окрестностях сварных швов напряжения сильно меняются на расстояниях порядка сантиметра. В то время как характерные размеры датчиков приборов составляют несколько сантиметров. Поэтому при измерениях происходит усреднение поля напряжений по некоторому характерному объему, определяемому конструкцией датчика прибора.

Таким образом, необходима разработка и создание экспериментальной установки, которая бы создавала в образцах механические напряжения достаточно общего вида. Для исследования эффектов усреднения необходимо в экспериментальной установке воспроизводить неоднородные поля напряжений σik (x).

Большой практический интерес представляют измерения напряжений в газопроводах. Так, было проведено определение напряжений в трубе большого диаметра под заданным давлением акусто-упругим методом с помощью прибора ИН-5101A. Отличие между экспериментально полученными напряжениями и теоретически рассчитанными для трубы данного радиуса и толщины составляет порядка 5% [5]. Цилиндрическая геометрия трубы выделяет две главные оси напряжения. Но это частный случай двухосных напряжений, хотя и крайне важный практически. Кроме того, в случае трубы направления двух главных осей тензора напряжений априорно известны.

Экспериментальная установка по созданию двухосного напряжения создана в Белоруссии [6] для калибровки прибора "Интроскан". В ней в образцах крестообразной формы воспроизводится двухосное напряжение растяжения. В центральной части образца поле напряжений постоянно. И для приборов, основанных на шумах Баркгаузена, этого достаточно, поскольку сигнал о напряжениях снимается с тонкого приповерхностного слоя образца. Это же справедливо и для приборов, основанных на эффекте магнитной анизотропии. Но для ультразвукового ИН-1051А постоянного, хотя и двухосного, напряжения недостаточно, поскольку вклад в регистрируемый сигнал дает вся толщина образца — происходит суммирование вкладов от напряжений по толщине. При этом существенна зависимость поля напряжений от координат x .

Отсюда возникают требования к будущей эталонной установке: установка должна создавать в образце любое поле напряжений σ_ik ( x ), которое может быть в реальных промышленных объектах. Если же это будет не так, и какие-то поля на установке не будут воспроизводиться, как это имеет место в [3], где создаются только одноосные напряжения, то калибровка приборов на таких установках недопустима [7], поскольку приведет при измерениях на реальных объектах к непредсказуемым результатам.

В [7, 8] была предложена конструкция эталонной установки, удовлетворяющей указанным выше требованиям. Установка представляет собой набор силовых гидравлических поршней, которые через крепежные устройства передают заданный вектор силы каждому из четырех углов образца в форме квадратной пластины. Эталонная установка предназначена для следующих задач.

• •    Моделирование в лаборатории полей напряжений, которые могут возникать в реальных промышленных конструкциях и объектах, и процесса измерений различными приборами неразрушающего контроля воспроизведенных тензорнозначных полей напряжений.

• •    Калибровка приборов, предназначенных для измерения механических напряжений.

Численному моделированию полей напряжений в этой установке посвящен следующий раздел.

МОДЕЛИРОВАНИЕ ЭТАЛОННОЙ СИЛОВОЙ

УСТАНОВКИ ДЛЯ СОЗДАНИЯ ПОЛЯ МЕХАНИЧЕСКИХ НАПРЯЖЕНИЙ

Итак, в установке создаются напряжения в стандартных образцах в форме квадратной пластины (рис. 4) Рабочей областью, в которой создаются напряжения, является центральная часть пластины, которую можно приближенно рассматривать как упругий слой. Поверхности этого слоя свободны от напряжений, т.е. на них выполняется

О = Q <7 = О, (7 = О. zz , xz , yz .

Поэтому значения этих компонент тензора напряжений близки к нулю и в толще образца. Будем считать, что эти компоненты тензора напряжений малы и в любых измеряемых конструкциях и не оказывают существенного влияния на результаты. Остальные три компоненты тензора напряжений σ_xx , σ_yy и σ_xy могут быть воспроизведены в средней части образца.

Поскольку в рамках линейной теории деформации изотропного упругого тела механические напряжения определяются прикладываемыми силами и не зависят от упругих характеристик материала [2], в качестве причины, вызывающей напряжения в образце, удобно использовать не смещения, задающие деформацию, а непосредственно силы, прикладываемые к образцу. Со-

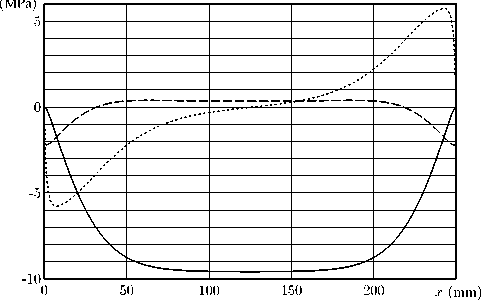
Рис. 5. Распределение напряжений в образце. Сплошная кривая — σxx, штриховая — σyy, пунктир — σxy, гласно принципу Сен-Венана, сбалансированные напряжения резко спадают с расстоянием, что позволяет не контролировать способ приложения сил, определяемый конкретным способом крепления силовой площадки к образцу. В качестве такового можно принять, например, болтовое соединение через отверстие в углу пластины. Итак, предлагается использовать силовую установку, позволяющую прикладывать к четырем углам пластины произвольные силы. Система сил, очевидно, должна быть сбалансированной, т.е. имеющей равную нулю равнодействующую.

Следовательно, к образцу прикладываются 4 силы (12 скалярных компонент), на которые накладывается 6 условий баланса. Итого имеем 6 произвольных величин. Возможно ли, варьируя эти величины, воспроизвести все компоненты тензора напряжений? Для ответа на этот вопрос было произведено численное моделирование при помощи пакета Abaqus.

Очевидно, что чем больше будет размер пластины, тем больше окажется и рабочая область. Однако образцы больших размеров трудно и дорого изготавливать, а также с ними трудно работать (ввиду их веса). В образцах необходимо создавать значительные напряжения, сравнимые с пределом упругости или даже текучести материалов, что важно для калибровки приборов, поскольку для практики необходимо определять напряженно-деформированные состояния объектов, близкие к возможным разрушениям. Для этого к образцам необходимо прикладывать большие силы, что, в свою очередь, ведет к увеличению установки, ее мощности и, соответственно, стоимости.

Оптимальной, на наш взгляд, является пластина размером 25 × 25 см. При таких размерах, как показывают расчеты (см. рис. 5), размер рабочей области, определяемой из требования отклонения

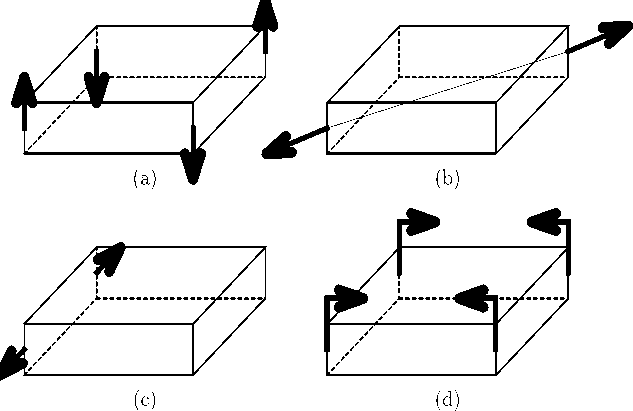
Рис. 6. Конфигурации сил (a), (b), (c) и моментов (d)

значения напряжений не более чем на 1 %, составляет порядка 5–7 см.

Всевозможные конфигурации сил с учетом симметрии сводятся к трем, изображенным на рис. 6, a, b, c. Поскольку к изгибу пластины приводит только конфигурация (a), был добавлен также вариант (d), в котором к углам пластины прикладываются вращающие моменты. Результаты расчетов напряженного состояния, вызванного действием сил в 1 кг, приведены в Приложении в табл. 1, 2 и 3 для пластин, имеющих толщину h = 5, 20 и 50 мм соответственно.

Отметим, что конфигурация (а) допускает точное решение в рамках теории тонких пластин [9]. Задача об изгибе пластинки ставится следующим образом: смещение срединной поверхности w ( x , y ) удовлетворяет бигармоническому уравнению

F = - D

/VV , dn

^{+ ( 1 -} v )

d ³ w d v d s²

I             я2^

M = D Aw-(1 -v)—r , | v     7Ss2 J

где D = Eh У ( 12 ( 1 - v ² ) )

— цилиндрическая жест-

кость, E — модуль Юнга, v — коэффициент Пуассона, ( n , s ) — нормаль и касательная к кромке. Нагружение в углах пластины может быть описа-

но

в терминах уголковых сил:

± L

d ² w d n d s

= F a ,

Л 2 П           I L L I

Aw = 0, x, y el--,-I-

Края пластинки свободны от перерезывающих сил и изгибающих моментов:

F ( x , - LI 2 ) = F ( x , LI 2 ) = 0,

M (x , - L/ 2 ) = M (x , L /2) = 0, x e ( - L/ 2, L /2) ,

F ( - LI 2, y ) = F (L[ 2, y ) = 0,

M ( - L /2, y ) = M ( LI 2, y ) = 0, y e ( - L /2, L /2 ) .

Для сил F и моментов M на прямолинейной кромке справедливы формулы [9]:

F | ± L + L | = - F c I 2,   2 J a

Здесь квадратными скобками обозначен скачок величины при переходе с одной кромки на другую через угол пластинки.

Заметим, что функция

w ( x , y ) = cxy

удовлетворяет и уравнению, и краевым условиям. При этом уголковые силы равны соответственно

F_c =± 2 D (1 - v ).

Отсюда находим

c =

6(1 + v ) F Eh ^{3     a} .

Значения коэффициентов в формуле (3)

h	С 1	С 2	С 3	С 4	С 5	С 6	С 7
5 мм	22.612	1.992	1.445	0.155	0.854	0.854	1.682
20 мм	22.826	1.998	6.689	-0.295	3.415	3.408	6.977
50 мм	23.524	0.672	38.76	-23.35	8.560	8.610	19.506

Деформации, отвечающие смещениям w , определяются формулами

dw        dw ux «--z, и «--z, uz « w.

xyz d x           d y

Тогда решению (1) будет соответствовать напряжение o =-6 Fah"3 z.

ветствующей таблицы 1, 2 или 3, a2 — значение σ в блоке (c), a3 — значение σ в блоке (c) xx                                                  yy и a4 — значение σxy в блоке (b). Аналогичным образом, линейно распределенные по толщине пластины напряжения определяются вектором сил ( Fa , Fd , fd')T формулами

Для пластины, имеющей толщину h = 5 мм, модель тонкой пластины дает значения σ на по-xy верхности, равные ±120 МПа, что согласуется с расчетом (см. Приложение, табл. 1) с погрешностью менее 1 %. Для пластины с h = 20 мм соответственно получаем значения ±75 МПа, что отличается от расчета на 4 %.

На основании произведенных расчетов можно указать, что компоненты σ , σ и σ во всех xz yz         zz случаях нагружения и для всех образцов пренебрежимо малы. Системы нагружения (b) и (c) позволяют воспроизводить значения оставшихся компонент тензора, практически равномерно распределенных по толщине пластины, а нагружения (a) и (d) служат для создания линейно распределенных по толщине напряжений. Наряду с вариантами (c) и (d) введем в рассмотрение также повернутые на 90° нагружения, которые будем обозначать (c') и (d'). Отвечающие им значения напряжений, очевидно, отличаются от напряжений при нагружениях (c) и (d) заменой oxx о oyy и сменой знака у σxy . Таким образом, в рамках линейной теории упругости, величины компонент тензора напряжений, возникающих при заданной комбинации нагружений, определяются по формулам

(^/az^ a^,/zz (s^xy /az J

Г о

( a 7

a ₅

a ₆ 0

a ⁶ 1 a 5

0J

F a

F к Fd' J

Обращая (2) и (3), несложно получить силы, которые требуется приложить для создания требуемых напряжений:

^d ° xx    ^d ^ y^L           ^ ^ x^     ^{d O yy}

¹ d 1   -    ⁺   2   -    ,    ¹ d'       2   -    ⁺   1   -    ,

О z О z              О z О z

F c = C 3 ^ xx + C 4 ^ yy - C S ^ xy , F c '= C 4 ^ xx + C 3 ^ ,, - C 5 G x _y , d o xy

F b    C 6 ° xy ,    F a C 7 Л .

Коэффициенты C j зависят от толщины пластины, их значения, рассчитанные по результатам моделирования, приведены в таблице.

( Oxx )

^σ yy

к oxyJ

f a a ,

( a 4

a ₂

a ₃ 0

a ³' a ²

0 J

fF FF к Fc' J

Коэффициенты матрицы в (2) берутся из таблицы, соответствующей образцу заданной толщины. Так, a 1 — это значение σ_xx в блоке (b) соот-

ЗАКЛЮЧЕНИЕ

Проведенные исследования показывают, что имеющиеся приборы неразрушающего контроля могут измерять лишь вполне определенные типы напряженного состояния механических конструкций. Так, ИН-5101А не чувствителен к напряжениям, возникающим при деформациях изгиба, а StressVision измеряет лишь разность главных напряжений в образце. Поэтому для достоверного измерения всех компонент тензора напряжений, по-видимому, нужно использовать комбинацию приборов, которые предварительно должны быть откалиброваны, и для такой калибровки нужна

более совершенная силовая установка, модель которой предложена в [7, 8] и рассчитана в данной статье. Кроме самой силовой установки необходимо предусмотреть создание набора (своего рода библиотеки) эталонных образцов. В данной статье мы ограничились лишь образцами простейшей прямоугольной формы. Однако, поскольку реальные конструкции могут состоять из балок различного профиля (швеллер, двутавр, труба круглого или прямоугольно сечения и др.), вероятно пона- добятся и соответствующие эталонные образцы. Отметим, что современные пакеты, аналогичные примененному в данной работе пакету Abaqus, позволяют проводить расчеты напряженного состояния подобных образцов и способов их нагружения с точностью, достаточной для решения задач, связанных с созданием эталонной установки, воспроизведением механических напряжений и калибровкой приборов.

ПРИЛОЖЕНИЕ

Табл. 1. Компоненты тензора напряжений (кПа) в центре 5 мм образца

Нагрузка (рис. 6)	z	σ xx	σ yy	σ xy
(a)	0	0.2	0.2	118859.0
	h /2	0.2	0.2	0.0
	h	0.2	0.2	–118859.0
(b)	0	624.9	624.9	1170.8
	h /2	624.9	624.9	1170.6
	h	624.9	624.9	1170.8
(c)	0	700.2	–75.3	0.0
	h /2	700.0	–75.1	0.0
	h	700.2	–75.3	0.0
(d)	0	8913.7	–785.7	0.0
	h /2	0.0	0.0	0.0
	h	–8913.7	785.7	0.0

Табл. 2. Компоненты тензора напряжений (кПа) в центре 20 мм образца

Нагрузка (рис. 6)	z	σ xx	σ yy	σ xy
(a)	0	–0.3	–0.3	7167.1
	h /2	–0.3	–0.3	0.0
	h	–0.3	–0.3	–7167.1
(b)	0	156.7	156.7	294.0
	h /2	156.7	156.7	293.4
	h	156.7	156.7	294.0
(c)	0	150.5	5.8	0.0
	h /2	149.8	6.6	0.0
	h	150.5	5.8	0.0
(d)	0	2207.4	–193.2	0.0
	h /2	0.0	0.0	0.0
	h	–2207.4	193.2	0.0

Табл. 3. Компоненты тензора напряжений (кПа) в центре 50 мм образца

Нагрузка (рис. 6)	z	σ xx	σ yy	σ xy
(a)	0	7.0	7.0	1025.3
	h /2	7.0	7.0	0.0
	h	7.0	7.0	–1025.3
(b)	0	64.5	64.5	117.6
	h /2	64.5	64.5	116.1
	h	64.5	64.5	117.6
(c)	0	41.9	23.0	0.0
	h /2	40.5	24.4	0.0
	h	41.9	23.0	0.0
(d)	0	850.9	–24.3	0.0
	h /2	0.0	0.0	0.0
	h	–850.9	24.3	0.0