Расчет монолитных железобетонных плит перекрытий высотного жилого комплекса с учетом физической нелинейности

Очевидно, что подобные расчеты очень трудо- и ресурсоемки. Даже не смотря на стремительное развитие компьютерных технологий в последние несколько десятилетий, большая часть всех расчетов строительных конструкций производится на основе упрощенных физических моделей [3; 4].

Сегодня в практике проектирования строительных конструкций, зданий и сооружений широко применяются программные комплексы компьютерного инженерного анализа (САЕ), основанные на методе конечных элементов (МКЭ). Данный метод является основным в современной строительной механике и позволяет в значительной степени автоматизировать расчет. Примерами комплексов САЕ являются пакеты программ ANSYS, NASTRAN, COSMOS, STARK, SCAD, ЛИРА, МОНОМАХ и другие [7]. Кроме того, многие из этих программных комплексов поддерживают технологию информационного моделирования (BIM). Она в последнее время все больше проникает в строительную отрасль, диктуя новый подход в проектировании инженерных объектов, основанный на создании полноценных информационных моделей. Данные передовые технологии разрабатываются с целью -приблизить теоретические расчеты к фактической работе конструкций и научиться прогнозировать их состояние с течением времени.

Цель работы - выполнить расчет и анализ напряженно-деформированного состояния монолитных плит перекрытий высотного жилого комплекса с учетом нелинейных свойств железобетона.

Для достижения поставленной цели необходимо было решить следующие задачи: создать пространственную модель конструктивной системы высотного жилого комплекса в ПК МОНОМАХ-САПР; выполнить линейный и нелинейный расчеты методом конечных элементов и анализ полученных результатов; изучить возможность использования упрощенных моделей для оценки действительной работы монолитных плит перекрытий с учетом физической нелинейности железобетона.

Результаты исследования и их анализ. Принимая во внимание вышесказанное, следует отметить, что расчет нелинейных систем является более сложной задачей по сравнению с решением линейных задач, основанных на обобщенном законе Гука, т.е. линейных зависимостях между напряжениями (с) и деформациями (г).

В данной работе нас интересует физическая нелинейность, при которой связь между напряжениями и деформациями записывается в общем виде так:

с = Е(г) г , где Е (г) - это матрица, характеризующая физические свойства материала.

Таким образом, учитывая физическую нелинейность, получаем систему нелинейных алгебраических уравнений, решение которой находится с помощью шаговых или итерационных методов. При этом среди известных алгоритмов расчета нелинейных систем отсутствует какой-либо универсальный способ. Эффективность каждого из методов зависит, главным образом, от типа и параметров проявляющейся нелинейности [5].

В специализированном программном комплексе МОНОМАХ-САПР 2013 реализована возможность учета физической нелинейности железобетона при расчете конструкций монолитных высотных зданий [8; 9]. Объектом наших исследований является 25-ти этажный жилой комплекс высотой 99,55 м со стилобатом и подземными этажами. В работе [10] приводятся архитектурные и конструктивные решения здания, а также результаты линейного и нелинейного расчетов пространственной модели монолитной конструктивной системы, выполненных в ПК МОНОМАХ-САПР.

На рисунке 1 представлена расчетная схема здания, которая состоит из оболочечных и стержневых конечных элементов. Общие расчеты при эксплуатационных нагрузках и воздействиях показали, что принятая монолитная несущая система обеспечивает прочность, устойчивость и пространственную неизменяемость высотного здания и его отдельных элементов. Полученные основные параметры конструктивной системы (горизонтальные перемещения верха, перекос этажных ячеек, прогибы элементов перекрытий, коэффициенты запаса устойчивости, средняя осадка, разность осадок и другие) не превышают предельно допустимых значений, установленных соответствующими нормативными документами [11–14].

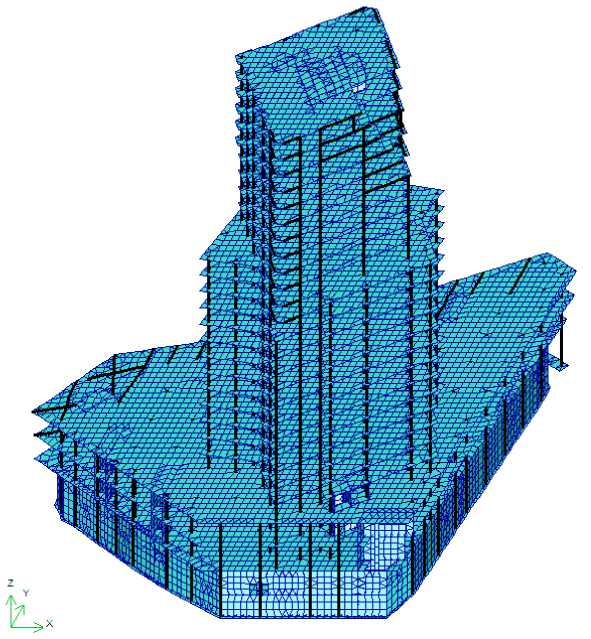
Рис. 1. Расчетная конечно-элементная схема здания.

В процессе нагружения железобетонных конструкций, как на стадии возведения, так и в процессе эксплуатации могут проявиться такие специфические особенности железобетона, как ползучесть или возникновение трещин в растянутых зонах. Вследствие чего, будет происходить изменение жесткостных характеристик элементов. Это приводит к перераспределению усилий, значительному увеличению перемещений по сравнению с линейно-упругим расчетом.

Нормативные документы ориентируют инженера на учет этих факторов при проектировании. В Сводах Правил Российской Федерации (СП 63.13330.2012, СП 267.1325800.2016, СП 430.1325800.2018) рекомендуется проводить расчет конструктивных систем в пространственной постановке с учетом физической нелинейности материалов [13 – 15]. Выполнение нелинейного расчета занимает значительное время и требует существенных вычислительных мощностей компьютеров, а также соответствующего программного обеспечения. В связи с этим, для учета вышеизложенных факторов в инженерных расчетах предлагается вводить понижающие коэффициенты при определении модуля упругости бетона и жесткости сечений. Согласно п. 8.2.4.15 СП 267.1325800.2016 [14] эти коэффициенты равны: 0,6 – для вертикальных сжатых элементов; 0,2 – для изгибаемых элементов при наличии трещин и 0,3 – при отсутствии трещин. Конечно, такое предположение только приблизительно учитывает снижение жесткости сечений в зависимости от характера напряженно-деформированного состояния элемента. В таблице 1 представлены значения начального модуля упругости бетона Е _Ь0 и с учетом понижающих коэффициентов - Е _{Ь т} для вертикальных и горизонтальных несущих конструкций здания.

Таблица 1

Снижение начального модуля упругости бетона согласно СП 267.1325800.2016

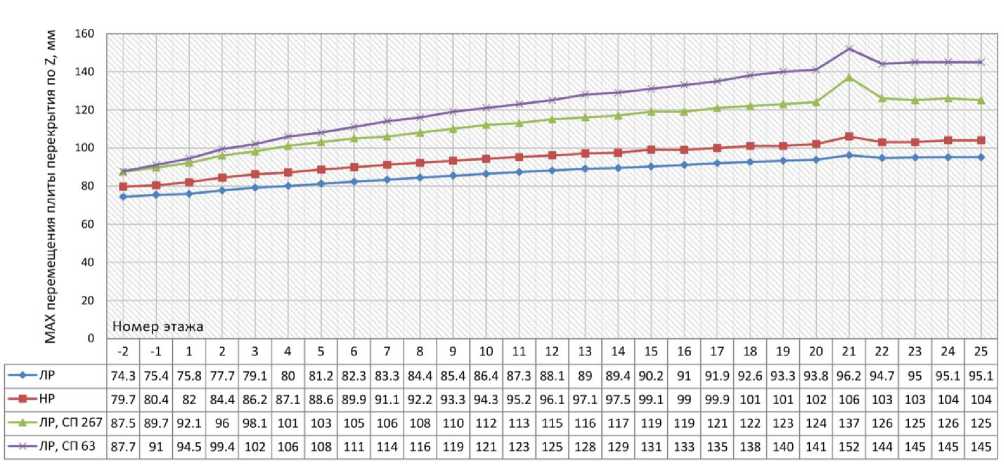
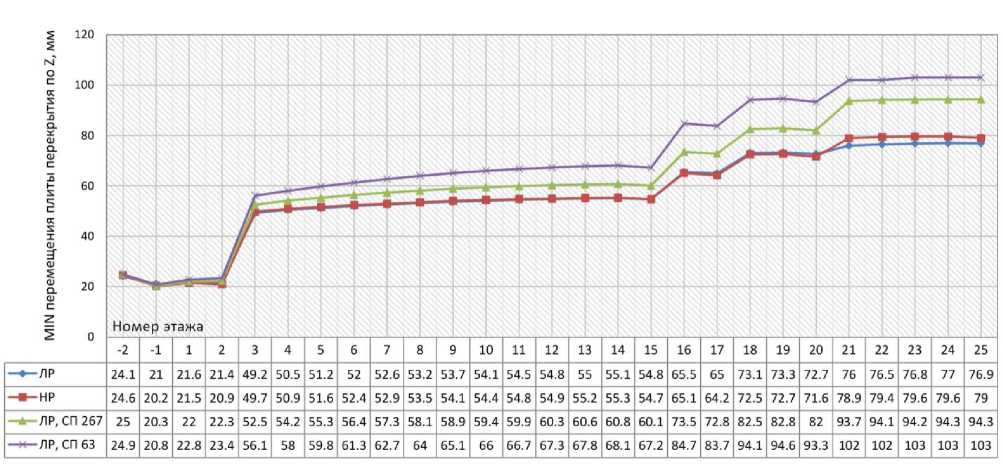
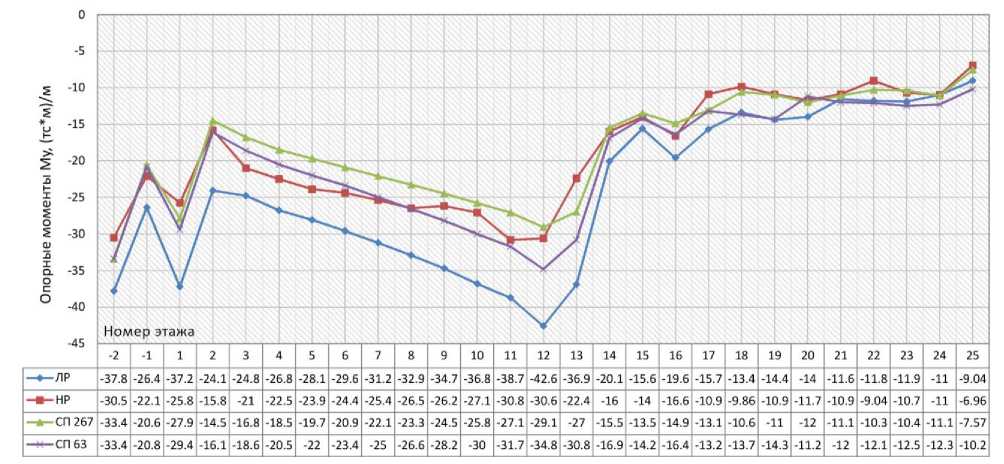
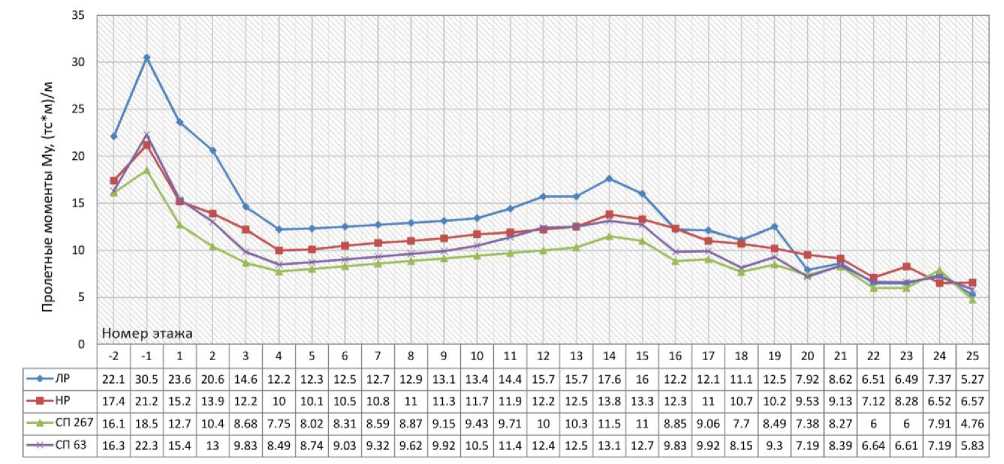
В соответствии с п. 6.1.15 СП 63.13330.2012 [13] при продолжительном действии нагрузки значение модуля деформаций бетона следует определять по формуле

Ebs = EboK1 +

где Рь,_сг- коэффициент ползучести бетона, принимаемый согласно п. 6.1.16; Е_Ь0- начальный модуль упругости бетона.

Вычисленные по СП 63.13330.2012 значения модуля деформаций бетона при продолжительном действии нагрузки приведены в таблице 2.

Таблица 2

Снижение начального модуля упругости согласно СП 63.13330.2012

Оба этих подхода позволяют оценить действительную ситуацию. Это можно продемонстрировать на примере следующих расчетов конструктивной системы здания.

Результаты определения напряженно-деформированного состояния монолитных плит перекрытий, полученные на основе линейных и нелинейных расчетов конструктивной системы здания, представлены на графиках (рис. 2 – 5). Здесь введены следующие обозначения: ЛР – линейный расчет; НР – нелинейный расчет; ЛР, СП 267 и ЛР, СП 63 – линейные расчеты при пониженных значениях модуля упругости бетона (табл. 1 и 2).

На рисунках 2 и 3 показаны графики экстремальных (максимальных и минимальных)

значений перемещений плит перекрытий -2 – 25 этажей соответственно.

Рис. 2. Графики максимальных перемещений плит перекрытий при различных методах расчета.

Максимальные значения перемещений, полученные при упрощенном расчете по рекомендациям СП 267.1325800.2016, превышают значения перемещений при линейном расчете (ЛР) на 15,09 % – 29,78 %. Результаты расчета, полученные по рекомендациям СП 63.13330.2012, превышают результаты линейного расчета (ЛР) на 15,28 % – 36,71 %. Меньшее превышение значений наблюдается при анализе минимальных перемещений плит перекрытий.

Рис. 3. Графики минимальных перемещений плит перекрытий при различных методах расчета.

На рисунках 4 и 5 показаны графики экстремальных значений опорных и пролетных изгибающих моментов в плитах перекрытий -2 ÷ 25 этажей соответственно, полученные при линейном и нелинейном расчетах.

Рис. 4. Сравнение опорных моментов (My) плит перекрытий при различных методах расчета.

Рис. 5. Сравнение пролетных моментов (My) плит перекрытий при различных методах расчета.

Выводы. На основании проведенных расчетов можно сделать следующие выводы:

• 1.    Снижение модуля упругости бетона и жесткости сечений согласно рекомендациям СП 267.1325800.2016 и СП 63.13330.2012 существенно сказывается на результатах вертикальных перемещений конструктивной системы в целом;

• 2.    Анализ результатов опорных и пролетных изгибающих моментов в плитах перекрытий показал следующие зависимости. Как при нелинейном расчете, так и при линейных расчетах с пониженными модулями упругости бетона, значения моментов в плитах уменьшаются практически на всех этажах. Более того, результаты нелинейного и упрощенных расчетов по рекомендациям СП 267.1325800.2016 и СП 63.13330.2012 очень похожи по характеру изменения от этажа к этажу и близки по значениям. Этот факт позволяет в некоторой степени утверждать, что предварительно оценить действительную работу железобетонных конструкций можно упрощенными методами, определяя жесткости сечений с помощью условных понижающих коэффициентов. Такие расчеты следует выполнять только лишь для начального анализа работы конструкций и конструктивной системы в целом;

• 3.    На последующих этапах расчета конструктивной системы, когда известно армирование железобетонных элементов, для получения более точных результатов необходимо производить расчет с учетом нелинейных жесткостей, учитывающих армирование, образование трещин и развитие неупругих деформаций в бетоне и арматуре.