Расчет на прочность самонастраивающегося гидравлического демпфирующего устройства

Эффективным средством торможения исполнительных механизмов мехатронных систем в условиях изменений масс и скоростей движения является использование самонастраивающихся гидравлических демпфирующих устройств роботов [1]. В работе [2] предложена система автоматизированного проектирования самонастраивающихся гидравлических демпферов, а в работах [3, 4] определены основные конструктивные параметры подобных устройств. При этом некоторые размеры определились из конструктивных соображений, без соответствующих расчетов. В настоящей статье рассматриваются вопросы определения конструктивных размеров самонастраивающихся гидравлических демпфирующих устройств из условий обеспечения достаточной прочности.

Расчетная схема самонастраивающегося гидравлического демпфера показана на рисунке 1. Максимальные напряжения и деформации будут возникать на основных элементах – корпусе 1 и штоках 2 и 3.

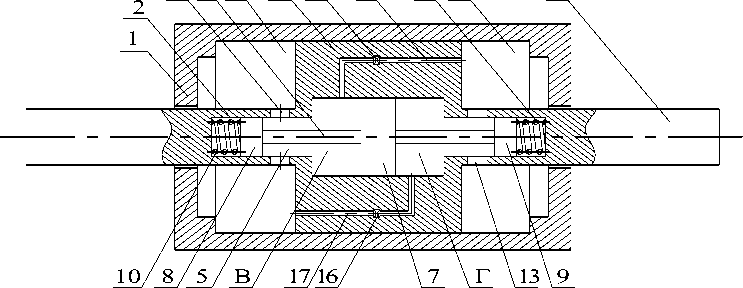
Рис. 1. Гидравлический демпфер:

1 – корпус; 2 и 3 – штоки; 4 – поршень; 5 – осевая полость; 6 – плунжер; 7, 8 и 9 – пояски; 10, 11 – пружины; 12, 13 – отверстия; 14, 16 – дроссели; 15, 17 – каналы; А, Б, В и Г – полости

Расчетная схема корпуса показана на рисунке 2. На этой схеме толщина цилиндрической оболочки предлагается постоянной, а нагрузка – осесимметричной [5, 6].

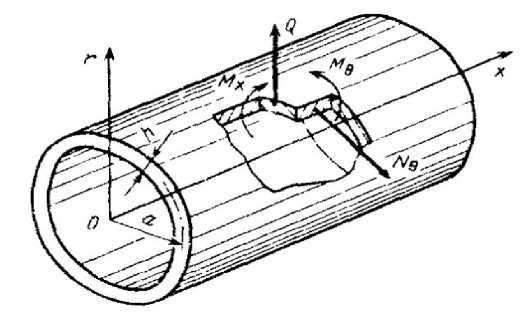
Рис. 2. Силовые факторы в сечениях корпуса демпфера

Получим уравнения радиального прогиба цилиндрического корпуса. Обозначив to(x) - ра- диальное перемещение точек срединной поверхности (положительному значению соответствует перемещение точек на окружность большего радиуса), будем иметь следующее дифференциаль- ное уравнение:

_ d ⁴ to    Eh            Eh                    d ² ( A T )

C,   + ^to = q + —^aT о ^- Cк ⁽¹ + ^v )tt| ^a т I,                   ⁽¹⁾

dx      a               a                      dx V h J

Eh ³

где C k =           - жесткость корпуса, H/см;

E – модуль упругости материала H/см²;

h – толщина корпуса, см;

a – радиус срединной поверхности, см;

q – распределенная нагрузка, приложенная к срединной поверхности корпуса, H/cм²

(например, внутреннее давление);

a - коэффициент линейного расширения, 1/⁰С;

T ₀ – температура срединной поверхности корпуса, ^oС;

A T - разность температур наружной и внутренней поверхности корпуса, ⁰С;

v - коэффициент Пуассона.

Распределение температур по толщине стенки предполагается линейным.

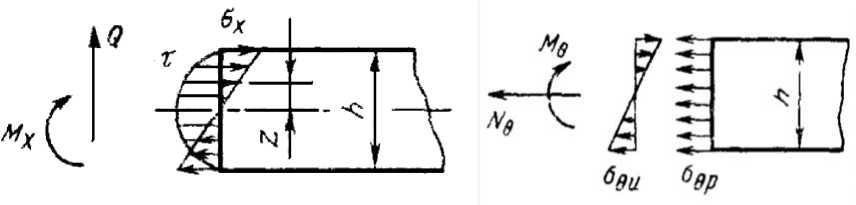
а – в поперечном                              б – в продольном

Рис. 3. Напряжения в сечениях корпуса демпфера

В поперечном сечении корпуса (сечении, перпендикулярном к оси (рис. 3) на единицу длины действуют:

перерезывающая сила, H/см, Q = C _к

d3 to dx3

d ( a A T dy V h

изгибающий момент, Н.см/см m = с xк

d2 to dx2

+ (1 + v )

a A T ^

h J

В продольном сечении (сечение проходящем через ось) на единицу длины приходятся:

растягивающая сила, H/см N ₈ = Eh |-- a T ₀ I ;                                   (4)

V a J

изгибающий момент, Н.см/см м _о = с_к

d ² го dx ²

+ (1 + v )

а A T ) h )

При отсутствии нагрева изгибающий момент в виде M _o = v M_x .

Напряжение изгиба в поперечном сечении распределяется по толщине стенки линейно:

с т

12Mx h3

z ,

где z – расстояние от точки до срединной поверхности корпуса.

Касательное напряжение в поперечном сечении определится выражением

Q ( 3 6 z ² )

^т = h ^ 2    h ² ;

В продольном сечении возникают нормальные напряжения растяжения

^С 0 р

и изгиба

с

⁰ И

N o

h

12 Мо z.

h ³

Из выражений (8) и (9) получим нормальные напряжения в продольном сечении:

с

о

No _ 12 Mo h      h3

h

В формулах (6), (7), (9) и (10) для наружного слоя корпуса демпфера z = —, для внутрен- h него z =    .

Рассмотрим расчетный случай, когда температурные напряжения отсутствуют ( Т ₀ = 0, A T = 0).

Общее решение однородного уравнения (1) представлено в виде го0( х) = e" вх (C1cos вх + C2sin вх),                 (11)

где величина в определяется равенством (11). Произвольные постоянные C1 и C2 находятся из граничных условий. Для полного решения к величине го0(х) следует добавить частное решение неоднородного уравнения (1). Например, при постоянном по длине внутреннем давлении

qa2. Eh q (рис. 4) это частное решение имеет вид го1 (х)

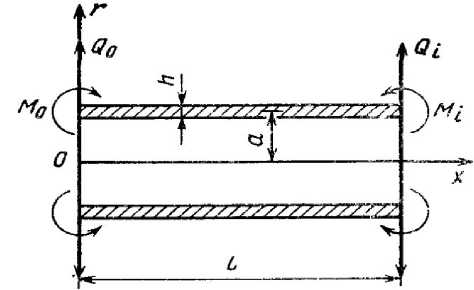
Рис. 4. Схема распределенной нагрузки

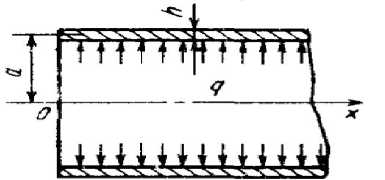
В случае расчета длинного цилиндрического корпуса, который показан на рисунке 4, d² го „ d 3 го „               , . qa²

х = 0;        = 0;       = 0; ГО ( х ) = 0; ^{го ( х} ) =      ; М_х ( х ) = 0.

dx2      dx3                       Eh x

Вычислив величину динамического напряжения, мы можем получить условие прочности в виде с т <  [ с ] , где [ ст ] — допускаемая величина нормальных напряжений. При этом толщина стенки корпуса определяется по формуле

h > Dp"

² Ь!^{[ с ]} - p

с + p

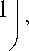
где p = 1,2pmax – расчетное давление, МПа, а диаметр штоки dsth

На основе полученных зависимостей была произведена проверка на прочность основных элементов гидравлического демпфера, рассматривалось в работе [3]: корпус: длина l = 0,071 м; внешний диаметр Dc = 0,027 м; толщина h = 0,006 м; а в штоке с поршнем: dsht=0,01 м, длина штока lsht = 104 мм (рис. 6 а).

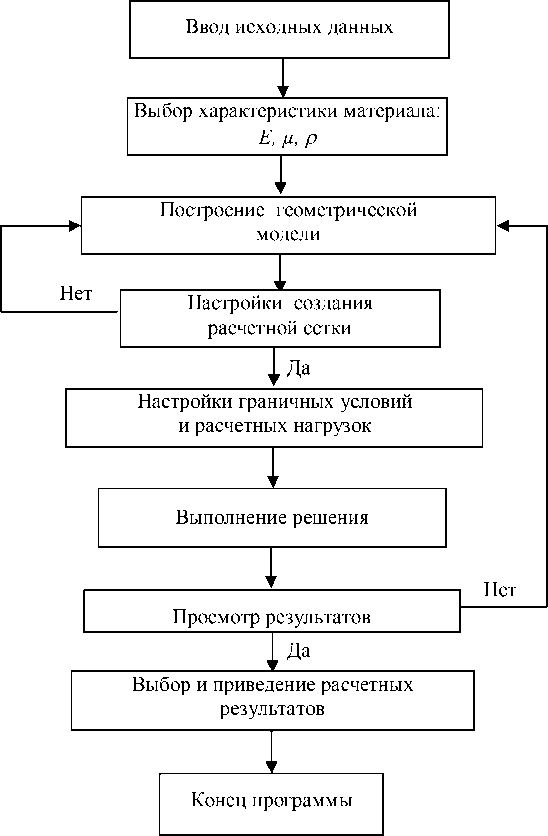
Рис. 5. Схема алгоритма расчеты на прочность в среде Ansys

Проверка производилась и с использованием программного вычислительного комплекса ANSYS версии 13 [7] на основе алгоритма, показанного на рисунке 5.

Для расчета приняты следующие параметры: модуль Юнга материала E = 2,1.e⁵ МПа; коэффициент Пуассона µ = 0,3; плотность ρ = 7850 кг/м³; допускаемое напряжение (предел прочности) на растяжение и сжатие легированной стали [σ] = 180 МПа [8, 9, 10].

На рисунке 6 б показаны расчетные сетки корпуса и штока. В этом случае выбран минимальный размер одной сетки 1 мм.

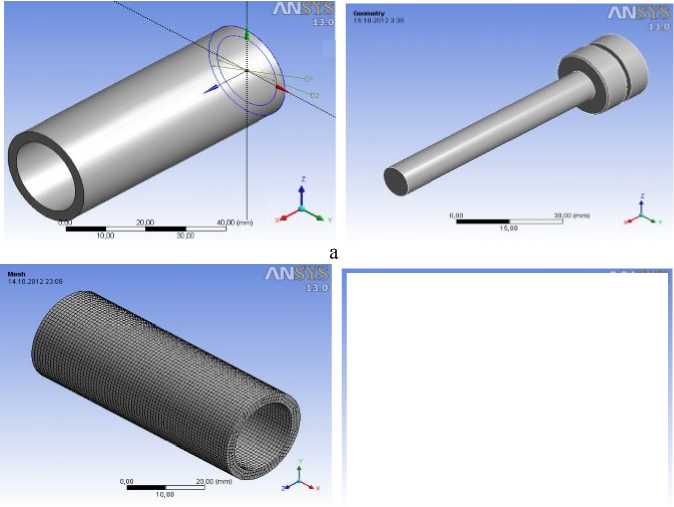
б а – трехмерные модели; б – расчетные сетки

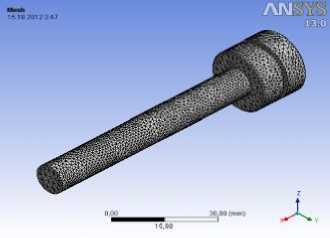
Рис. 6. Модель корпуса и штока с поршнем демпфера:

а

б

в

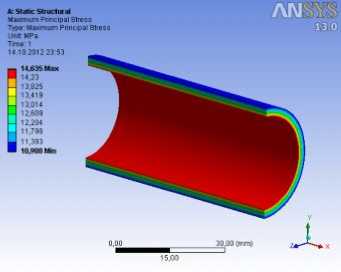
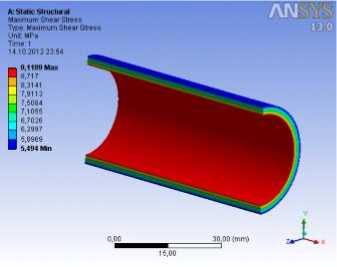
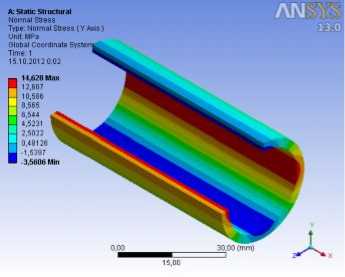
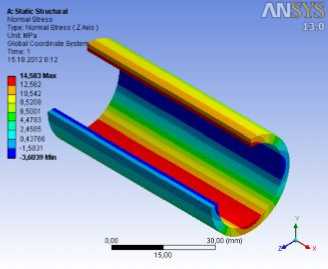
Рис. 7. Состояния напряжений в корпусе и штоке:

а – максимальные главные напряжения;

г б – максимальные касательные напряжения;

в – нормальные напряжения по оси y σ _y ;

г – нормальные напряжения по оси z σ _z

б

в

а – максимальные главные напряжения;

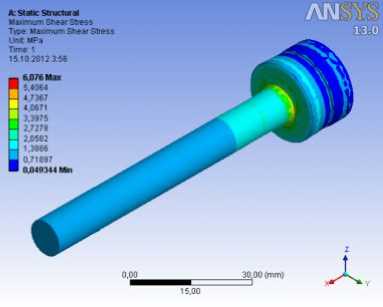
Рис. 8. Состояния напряжений в штоке:

б – максимальные касательные напряжения;

в – нормальные напряжения по оси y σ _y ;

а

г – нормальные напряжения по оси x σ _x

б

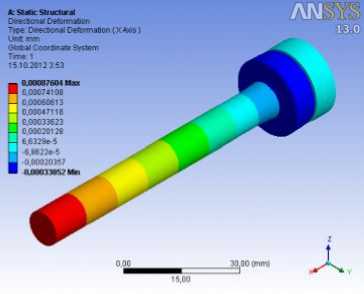
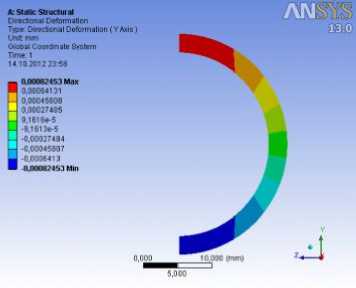
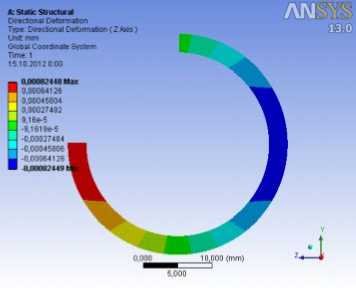
Рис. 9. Состояния деформации корпуса и штоки:

а – радиальная деформация по направлению z; б – радиальная деформация по направлению y; в – осевая деформация по направлению x

Результаты расчетов приведены на рисунках 7–9. Из этих графиков получены максимальные значения напряжений и максимальные значения деформаций точек, возникающих в корпусе: главное напряжение 14,635 МПа; касательное напряжение 9,1199 МПа; нормальное напряжение по оси y σ _y = 14,628 МПа и по оси z σ _z = 14,583 МПа; радиальная деформация δ _r =0,824.10³ мм; а в штоке соответственно: 14,354 МПа; 6,076 МПа; σ _x = 11,404 МПа; σ _y = 6,4883 МПа; осевая деформация δ _x = 0,876.10^-3 мм.

Из этих результатов видно, что максимальные значения напряжения и деформации точек в основных деталях демпфера оказались меньше допустимых граничных напряжений и деформаций материала демпфера.

Таким образом, исследования показали, что детали обладают достаточной прочностью. В то же время некоторые детали имеют небольшой запас прочности. На основании проведенных исследований программа автоматизирования расчета была дополнена алгоритмами выбора конструктивных параметров самонастраивающихся гидравлических демпферов.