Расчет на устойчивость деревянных арок с учетом нелинейной ползучести

УДК 624.04                                               

Введение. Древесина относится к материалам, проявляющим свои нелинейные свойства, как при кратковременных, так и длительных воздействиях. Большинство существующих реологических моделей дерева устанавливает его мгновенные свойства на основе закона Гука, однако для сжатой древесины характерна нелинейная диаграмма упругопластического типа [3]. Впервые вопросы совместного учета мгновенных упругопластических свойств древесины и ее ползучести стал исследовать К. П. Пятикрестовский. Указанные свойства он объединил на основе метода длительного модуля деформации [4–7]. В данном методе уравнение ползучести содержит время в явном виде, что существенно ограничивает его использование в случае сложных режимов нагружения и переменных нагрузок. В литературе имеется значительное количество публикаций по совместному учету ползучести и мгновенной нелинейности деформирования древесины при расчете сжатых стержней [8–14]. В частности, в работе [8] рассматривается вопрос применимости к описанию нелинейной ползучести древесины принципа суперпозиции Больцмана. В работе [9] для сжатых стержней проводится сопоставление теоретических расчетов с экспериментальными данными, а в статье [10] помимо сжимающей продольной нагрузки учитывается поперечная нагрузка. В работах [11–13] задача устойчивости решается для стержневых элементов в составе рамной конструкции. В статье [14] для сжатых деревянных элементов выводится длительная критическая сила с учетом нелинейной ползучести.

Проблема расчета с учетом ползучести и мгновенной нелинейности деформирования актуальна не только для отдельно взятых стержней и рам, но и для таких стержневых систем, как арки. Целью настоящей работы является разработка методики расчета арочных конструкций с учетом нелинейных свойств материала при кратковременных и длительных воздействиях, а также геометрической нелинейности.

Материалы и методы. В качестве соотношения, определяющего связь между напряжениями и деформациями, воспользуемся уравнением вязкоупругопластической модели наследственного старения:

. ( t ) =       - к и- )^ d r ,

Механика

E 0 ⁽ t )       ^т о                  ^{d T}

Данное уравнение впервые было предложено в [1] для моделирования нелинейной ползучести бетона. Функция к о) здесь устанавливает связь между напряжением и мгновенной деформацией, C ( t,T ) — мера ползучести. Диаграмма напряжения-деформации сжатой древесины при кратковременном нагружении хорошо аппроксимируется формулой Герстнера [15], имеющей вид:

• а = E £-- °- £ 2 .

⁰   4 R

Сжимающие напряжения в формулу (2) подставляются со знаком «+». При растяжении для дерева имеет место линейная диаграмма вплоть до разрушения. Выразив из (2) деформацию через напряжение, получим:

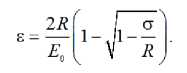
На основе (3) функцию напряжений f (σ) можно записать в виде:

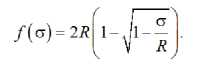
Для меры ползучести древесины воспользуемся формулой, предложенной в работе В. А. Зедгенидзе и И. Е. Прокоповича [2]:

C ( t , т ) = ( C о + A o e -”) ^ 1 — Be -’■< t ^—T)J , где C o = 2,87-10^-5 МПа^-1, A о = 10,95-10^-5 МПа^-1, B i = 1, y = Y i = 0,15 сут^-1.

Уравнение (1) можно представить в форме:

ст ,    .

е = +е , E где E = ^0СТ — секущий модуль, е* =— f Гст(тAn^CItilldT — деформация ползучести. f (ст)                                      T0               а

Для меры ползучести в виде (5) деформацию ползучести можно записать в виде суммы двух составляющих:

tt

е * =е * +е2, е * = у C 0 B , J f [ о ( т ) ] e ^{—Y (} t "’ d т , е 2 = A y J f [ о ( т ) ] ed т .

^T 0

^T 0

Дифференцируя по времени (7), получим выражения для скоростей роста каждой составляющей:

^ = y(CоBf[о(t)] — е*); ^ = Af[ст(t)]е

< t .

Выведем на основе (6) связь между внутренними усилиями и деформациями для элемента при совместном действии продольной силы и изгибающего момента. Модуль упругости будем предполагать функцией от координаты у , которая по высоте сечения меняется от - h /2 до h /2. На основе гипотезы плоских сечений полную деформацию запишем в виде:

е = е 0 + у X ,

.                      d2 v где £о — деформация среднего слоя, % =---изменение кривизны.

dx ²

Подставим далее (9) в (6). Выразив о через е, получим:

ст = E ( у ) ( e

^^^^^^s

^е * ) = E ( У ) (^е 0 + у % ^— е * ) .

Продольная сила и изгибающий момент в элементе связаны с напряжением через следующие интегральные зависимости:

M = J ст ydA ; N = J CT dA .

AA

Здесь A — площадь поперечного сечения стержня.

Подставим (10) в (11) и преобразуем полученные равенства к матричной форме:

N МDК ° . M J [ ]1%

—

'N* I M * I ,

где N* =J Е (y) eSA, M* = J Е( у) у е dA, [ D ] = AA определяются по формулам:

EA ES

ES EI

— матрица приведенных жесткостей, которые

EA = J e ( y ) dA, ES = J E ( y ) ydA, EI = J e ( y ) У dA.

A

A

A

Решение задачи с учетом физической и геометрической нелинейности авторами будет выполнено при помощи метода конечных элементов. Используется стержневой элемент, приведенный на рис. 1. Осевая деформация при учете геометрической нелинейности представляет сумму линейной и нелинейной составляющей:

_lndu 1 dv ₂ e_o — e_o +e_o — + ( ) . 0 00

dx 2 dx

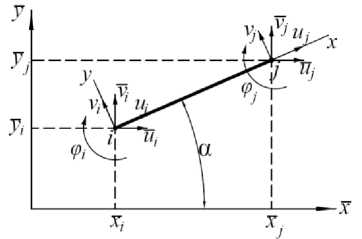
Рис. 1. Стержневой конечный элемент

Для получения системы уравнений МКЭ воспользуемся вариационным принципом Лагранжа. Потенциальная энергия деформации (ПЭД) записывается в виде:

П — 1 J°e eldV — 1 JE (y )(e 0 +£0 + y x-e* )2 dV.(15)

2V2

где e el — упругая деформация, равная разности между полной деформацией и деформацией ползучести.

Запишем (15) как сумму четырех интегралов:

П — ¹   E(y ) e'fe'+e " + yx-e * dVV + Ey e n fe' + e n + yx-e') dV+

• 2 V VV

+JE(y) yx(e0 + en + yx-e*) dV-JEy)e* (e0 +e0 + yx-e*) d V | V                                         V/

Первый интеграл в (16) запишется в виде:

fE(yAe' (e' + e„' + yx-e*}dV — fel E(yAfe'+ yx-e*\dAdx + 00   0                00

V 0 A

/                                                          //

+Je0 -en Je(y) dAdx — Je0AdX+Je0 -e0 • EAdx, 0A00

где l — длина конечного элемента.

Второй интеграл в (16) представим в следующей форме:

JE(yК (e0 + e0n + yx-e*)dV — Je0 - e n JE(y)dAdx+ JE(y)(e0)2 dV+ V0

ll

+ J e 0 -x j E ( y ) ydAdx - J e n J E ( y ) e*dAdx,

0 A 0 A

Вторым слагаемым в правой части (18) можно пренебречь, учитывая его более высокий порядок малости. Третий интеграл в (16) записывается в виде:

l

J E ( y ) y x ( e 0 +e n + y x-e * ) dV — J x J e ( y ) y ( e 0 + yx-e * ) dAdx +

V	l                  l 0 A l                                                                             (19) + J e 0 x • ESdx — J M x dx + J e 0 x • ESdx . 0   00

Четвертый интеграл в (16) представим в следующем виде:

l

J E ( y ) e * ( e 0 + e n + y x-e * ) dV — J x J E ( y ) ye dAdx+

V 0 A

+_[e 0 Je *E (y) dAdx -J(e * )2 E (y) dV + _[en Je *E (y) dAdx —

0AV0

lll

• — J x M dx + J e 0 N * dx + J e n N * dx - J ( e * )² E ( y ) dV .

000 V

Слагаемое J (e * )² E ( y ) dV при минимизации по вектору узловых перемещений обратится в нуль.

V

Окончательно выражение для ПЭД примет вид:

llllll

П — —(J e Nddx + 2^ e ' _oe n EAdx + J m x dx + 2j e n x ESdx -Jx M*dx -Je l, N * dx +                     (21)

2 0 ⁰            0 ⁰⁰            00 ⁰             00 ⁰

Механика

+2 j &Xdx ) = 0

^x + N av j ^e 0 dx ,

где Nav = б0EA + xavES — N* — средняя продольная сила в элементе, хav — среднее изменение кривизны элемента.

С учетом (12) формула (21) примет вид:

l

'.

^п = 3 j { б }   [ D ]{ = } - ²

2 0

■ N* 11         L , dx + N б„dx ,

M J I ^av j ⁰    ’

где ^{ б ^{} Т} = ^{ б 0 X^} T .

Для перемещений конечного элемента примем следующую аппроксимацию:

“₂ ^— “

“ ( x ) = “ + — x ;

v ( x ) = a₁ + a₂ x + a₃ x ² + a₄ x ³;

dv                    2

m l x ) = =a, + 2a₃ x + 3a. x .

^{v 7} dx ^{2       3        4}

Коэффициенты полинома (24) определяются путем подстановки в (24) и (25) координат узлов:

'a . ^ a .

a.

a

a

IФ

^V 2

- ^ф 2 /

-

Из (26) вектор { a } = {a ,   a₂

О^

выражается следующим образом:

{a} =

a3

0	0 "	— 1	I v 1 1
0	0		Ф 1
1 2	1 3		v 2
2 l	3 1 2 _		(.Ф 2 7

3 —

"ё

—

l

—

1 —

I £ ё

( “ 7 v 1

:

= [ Ф ]{ ^ }-

С учетом (27) формула (24) примет вид:

v = { ^T }{ U } ,

Вектор {е} запишем в форме:

{б} =

। d“ dx d2 v

л

—

dx ² 7

где T = { 1

—1/ 1      0

^d ‘ { ^T }

—

dx2

x

x ²

x ³ } [ Ф ] .

1/ I 0 0

• { и } = [ B ] { U } ^-

После подстановки (29) и (28) в (22) ПЭД запишется в виде:

П = !{ U } 4 [ В ] ^T [ D ][ В ] dx {U } — { U } T h В ] ^T dx ^f N J + { U } T N • ¹ f d^ }- d^ dx { U } . 2        -^{[ ] [ ][ ]    { } { }} j ^{[ ]}      [ m * J ^{1 1 av} 2 j dx dx ^{{ }}

После минимизации функционала Лагранжа по вектору узловых перемещений приходим к системе уравнений следующего вида:

l где [K] = j[B]T [D][B]d

—

([ K ]+[ Kg ]){U }={ F}+{F*}, rd{T}T d {T} матрица жесткости, \ K I = Nav---—- dx gJ    " Jo  dx dx

—

геометрическая матрица

, ..    V         f N* 1

жесткости, { F } = [ B] ^T dx      — вклад в вектор нагрузки деформаций ползучести, { F } — вектор внешних

I M

узловых сил.

Решение физически и геометрически нелинейной задачи осуществляется при помощи метода Ньютона-Рафсона. Первым этапом производится расчет при t = 0. Приращение нагрузки выполняется квазистатически небольшими порциями с последовательным вычислением дополнительных перемещений узлов, которые обусловлены невязкой сил, корректировкой на каждом шаге касательного модуля упругости и координат узлов.

Далее временной интервал, на котором выполняется расчет, разбивается на конечное число шагов по времени. Расчет на ползучесть выполняется аналогично расчету на статическую нагрузку. Приращение деформаций ползучести на шаге t + Δt может быть определено с использованием метода Эйлера ** **

Д _е * = |^L + ^2 I Дt .                                           (32)

(5 t   at)

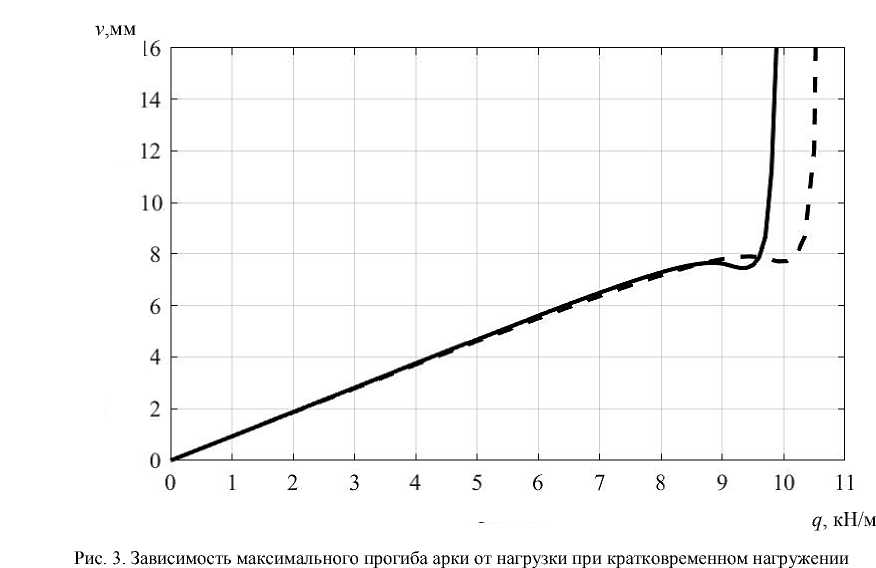
Результаты исследования. Представленные уравнения и алгоритм расчета реализованы авторами в виде программы в среде Matlab. Был выполнен расчет шарнирно неподвижно опертой по концам арки параболического очертания под действием равномерно распределенной по длине нагрузки (рис. 2) при следующих исходных данных: E 0 = 1,48⋅10⁴ МПа, R = 55 МПа, L = 16 м, f = 3,2 м. Поперечное сечение арки принималось прямоугольным с размерами b = 10 см, h = 15 см. Арка разбивалась по длине на 40 конечных элементов, по высоте сечение делилось на 100 отрезков, количество шагов по времени принималось равным 600, а по нагрузке — 200. Максимальное количество итераций на каждом шаге — 20. На рис. 3 показан график зависимости максимального прогиба от нагрузки. Штриховой линии соответствует расчет в упругой постановке. Для контроля правильности результатов решение упругой задачи также выполнялось в программном комплексе ANSYS с использованием стержневых конечных элементов BEAM 188. Количество конечных элементов принималось такое же, как и в Matlab. Существенной разницы результатов выявлено не было. При расчете в упругой постановке резкий рост перемещений, соответствующий потере устойчивости, наблюдается при q = 10,5кН/м, а при учете мгновенной нелинейности деформирования — при q = 10кН/м.

q

H 11 и 11111 m 1 и 1 m

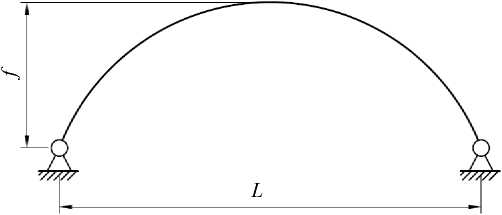
Рис. 2. Расчетная схема конструкции: q — распределённая нагрузка на арку, f — стрела подъёма арки, L — пролет арки

Механика

Расчет с учетом ползучести для данной арки показал, что даже при нагрузках, достаточно близких к мгновенной критической, рост перемещений носит ограниченный характер. На рис. 4 приведен график роста во времени прогиба в середине пролета при нагрузке q = 8кН/м. Штриховой линии на данном графике соответствует решение в вязкоупругой постановке. Существенной разницы в результатах не выявлено.

Также при указанных выше исходных данных был выполнен расчет трехшарнирной арки с промежуточным шарниром в середине пролета. В этом случае мгновенная критическая нагрузка оказалась существенно ниже. При расчете в упругой постановке она составила 4 кН/м, а с учетом мгновенной нелинейности деформирования — 3,3 кН/м. Как и в предыдущем примере, даже при нагрузке, достаточно близкой к мгновенной критической, ползучесть носит затухающий характер. Кривые изменения во времени максимального прогиба при q = 3кН/м приведены на рис. 5. Обозначения такие же, как и на предыдущем графике.

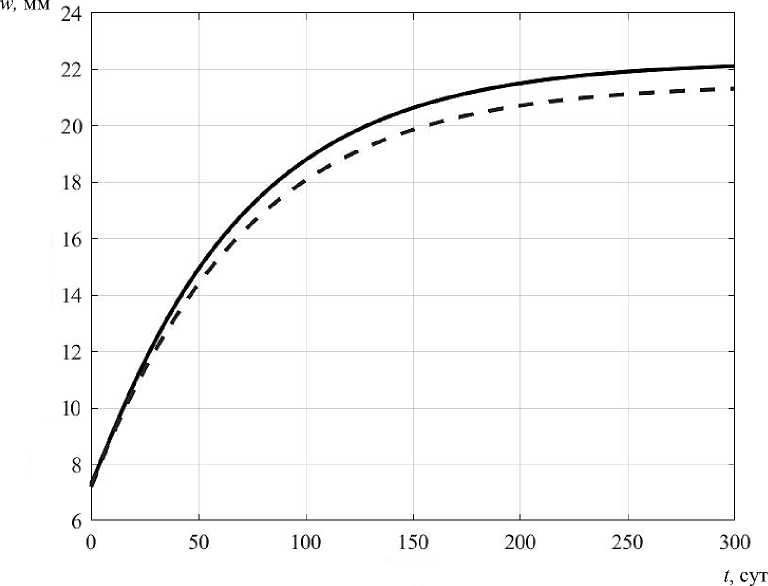
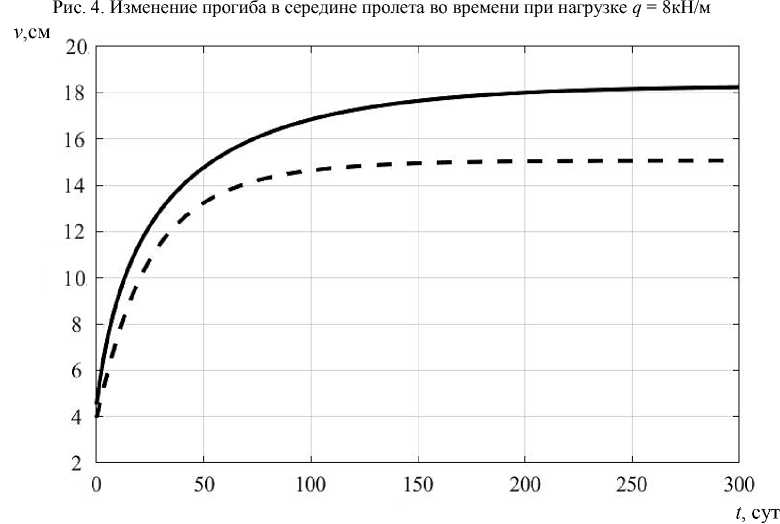
Рис. 5. Рост во времени максимального прогиба для арки с промежуточным шарниром в середине пролета при q = 3 кН/м

Обсуждение и заключения . Полученные уравнения и разработанная методика являются универсальными и допускают применение произвольных зависимостей между напряжениями и мгновенными деформации, а также произвольных выражений для меры ползучести. Это позволяет производить расчеты конструкций, изготовленных не только из дерева, но и из любого другого материала. В результате проведенного анализа ползучести деревянных арок установлено, что в отличие от сжатых стержней, для них ползучесть носит ограниченный характер даже при нагрузках, близких к мгновенной критической.