Расчет надежности отказоустойчивых архитектур программного обеспечения

Программное обеспечение (ПО) является неотъемлемой частью современной жизни. Практически любые электронные устройства содержат ПО того или иного вида. Без соответствующего программного обеспечения не возможно представить промышленное производство, системы образования и здравоохранения, финансовые и государственные учреждения. Программное обеспечение является важной частью систем управления и обработки информации. Однако, несмотря на столь широкое применение ПО, нельзя утверждать, что оно является абсолютно надежным. Даже простое ПО, применяемое на домашних персональных компьютерах, может содержать ошибки проектирования, которые могут стать причиной отказа либо программы, либо компьютера. Последствия таких отказов минимальны, как правило, это перезагрузка компьютера и последующая замена ПО на более совершенное. В то же время отказ программного обеспечения, применяемого в критических системах, таких как системы автоматического управления, телекоммуникационные системы и другие, может привести к большим человеческим и экономическим потерям.

В зависимости от сложности программного обеспечения и целей его использования к ПО предъявляются различные требования по уровню надежности [1]. Надежность ПО должна быть тем больше, чем сложнее проблемы оно решает.

Так как предполагается, что любое ПО может содержать ошибки то, необходимо использовать средства проектирования, которые бы обеспечивали устойчивость ПО к сбоям его компонентов [1]. К таким средствам относятся отказоустойчивые архитектуры, целью которых является предотвращение отказов программного обеспечения [1; 2].

Методами построения отказоустойчивых архитектур являются N-вариантное программирование (NVP) и блоки восстановления (RB) [2]. Оба метода относятся к муль-тиверсионным методам обеспечения отказоустойчивости, которые основываются на использовании двух или более версий компонентов программного обеспечения. Версии реализуются с помощью различных алгоритмов и разными проектировщиками, что уменьшает вероятность появления одинаковых ошибок. Поэтому если одна версия отказывает на специфических данных, то, по крайней мере, одна из альтернативных версий должна обеспечить корректный результат. Показателем, характеризующим версии, служит вероятность безотказной работы

(надежность версий) или в случае экспоненциального распределения времени безотказной работы - интенсивность отказов.

Для расчета надежности NVP и RB архитектур будем использовать основные теоремы теории вероятности, а именно, основываясь на теореме сложения и теореме умножения [3,4], можно найти выражение для вероятности безотказной работы программного обеспечения. Будем рассматривать такие версии ПО, которые не подлежат восстановлению в случае отказа. Такой случай характерен для ПО, применяемого на космических и воздушных аппаратах.

Расчет надежности NVP архитектуры . В соответствии с общей спецификацией различными командами разработчиков рассматриваются несколько версий компонентов программного обеспечения. Эти версии выполняются параллельно на отдельных компьютерах [2]. Результаты их работы сравниваются с помощью алгоритма голосования, и уже он выдает согласованный конечный результат. Результат голосования будет тем точнее, чем больше версий выдадут верный результат. Например, голосование абсолютным большинством требует, чтобы строго больше половины версий вернули идентичный результат.

Построим модель для N-вариантного программного обеспечения с тремя версиями и алгоритмом голосования - голосование абсолютным большинством. Введем следующие обозначения: R - надежность ПО,_р₁,_р₂,_р₃ - вероятности безотказной работы версий,_р ^ - вероятность безотказной работы алгоритма голосования и N- число версий.

В соответствии с выбранным алгоритмом голосования ПО будет работать правильно только в том случае, если одновременно откажет не более одной версии. Рассмотрим событие^ - программное обеспечение работает. Это событие выполняется при одном из следующих условий:

событие В - версии 1и 2 вернули верный результат, версия 3 отказала;

событие С - версии 1и3 вернули верный результат, версия 2 отказала;

событие D - версии 2и 3 вернули верный результат, версия 1 отказала;

событие Е - все версии вернули верный результат.

События В, С, D и Е несовместны, поэтому по теореме сложения вероятностей вероятность события^ есть р(А) =р(В)+р(С)+рф)+р(Е).

Вероятности событий В, С, D и Е с учетом алгоритма голосования находятся по теореме умножения вероятностей для независимых событий [2]:

р(В) ^р^р₂(^-р₃)р_у,р(С) -р₁р₃(^-р₂)р_у, P ^{( D )} ^р 2 р 3 ^{(1 -} р1' ) р у ^,р^{( Е )} ^р^Р с.

Тогда вероятность безотказной работа ПО равна

^R =р ⁽ А ⁾ рЧ> И. '!>!>. ⁺ рр ^{- 2} р д . р^-

Аналогичные рассуждения проводятся для любого N, так для ПО с пятью версиями отказ наступит, если одновременно откажут более двух версий. Вероятность безотказной работы для N= 5 равна

^R =.?>№№ ^тлХ^1-^ Хр^-Хр^Х ⁺ ^рр^^рр ^ р 1 ^(1-р "^р р ^ 5 ' Хр^^^ ^{+ +} ЕРХ^р^Х' ) ⁺р 1 р 2 ^{(1 -} р - ⁾р 4 ^{(1 -} р 5 ^{) +}

Х^хХр^х) ⁺ ХрМр^¹^ ⁺ ♦раД-р-Х^рДЛ ⁺р 1 ^{(1 -} р ₂ ⁾р - ^{(1 -} р 4 ⁾р 5 ⁺ ЧХМр-^^Х ⁺Р 1 ^{(1 -} р 2 ^{)(1 -} р - ) рР 5 ⁺ Ч^рМХрз^р ⁺ Хр^^рр^.

Если версии имеют одинаковую вероятность безотказной работы, то надежность ПО рассчитывается по формуле

N - k

R = Pv 5 CN+ipk+i (1 - p)N-k-i, i=0

где k = ceil((N+1)/2) - минимальное число версий, возвращающих верный результат, ceil() - оператор округления до наибольшего целого числа, С - число сочетаний.

Алгоритм голосования абсолютным большинством является достаточно простым для реализации, но он не учитывает историю предыдущих отказов и вероятность отказов самих версий. Наиболее эффективным будет такой универсальный алгоритм, который сможет выбрать правильный результат даже при одном верном решении. Рассчитаем надежность ПО с тремя версиями при таком алгоритме голосования. ПО будет работать корректно, если: все версии вернут верный результат, две любые версии вернут верный результат, а одна откажет и одна версия вернет верный результат, а две другие откажут. Надежность ПО находят по следующей формуле

R Мд рр. ' рр ⁽ - р¹' -Х ^{(1 -}р₂Х ⁺ Х-р>-рз ⁺ +р 1 ^{(1 -}р₂ ^{) (1 -}р - ^{) +} ХрМХр-^-) ⁺ GX) ^{(1 -}? 2 ⁾ ^^р з ⁾ .

При таком алгоритме голосования удобно перейти к противоположному событию (рассматривать случай, когда ПО откажет), так как оно распадается на меньшее число вариантов. Отказ ПО произойдет после отказа всех версий. Надежность ПО находят по формуле

R ^н^а-^а-^з)).

Для любого N надежность программного обеспечения:

R = P v

)

N

1 - П (1 - р.

i = 1

Зависимость надежности ПО от надежности его версий и алгоритма голосования представлена на рис. 1, при условияхр = р2=р3 =р4"= р5= р,N:= 5,рк=0,9, кривая 1 - используется универсальный алгоритм голосования, кривая 2 отображает голосование абсолютным большинством. Как и следовало ожидать, надежность ПО с универсальным алгоритмом голосования выше. Такой алгоритм может быть основан на методе изменяющихся вероятностей, а вероятности безотказной работы версий использоваться как начальные условия для метода.

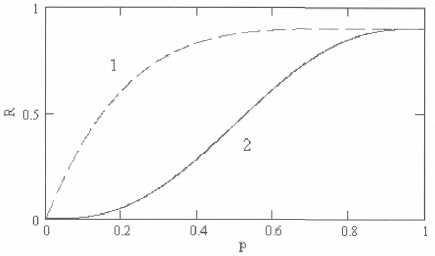
Рис. 1. Надежность ПО в зависимости от алгоритма голосования

График надежности ПО с алгоритмом голосования абсолютным большинством при изменении числа версий (надежность версий одинакова,^ = 0,8,рг= 0,9) представлен на рис. 2. С ростом числа версий надежность ПО стремится к надежности алгоритма голосования. В таком случае изменение надежности ПО произойдет только при изменении характеристик версий или алгоритма голосования. При выборе этого алгоритма голосования следует использовать нечетное число версий, это обеспечивает оптимальное соотношение числа версий - надежность.

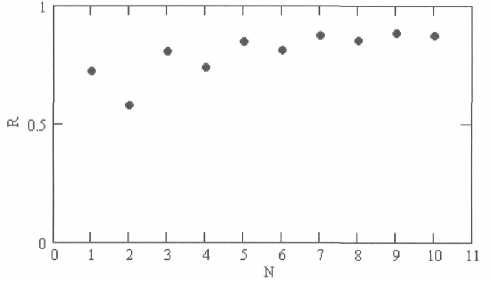
Рис. 2. Надежность ПО в зависимости от числа версий

В том случае если известна интенсивность отказов версий л, то р. заменяется на [4] p. = e ^r i t . Все формулы остаются справедливыми.

Надежность программного обеспечения с блоками восстановления . Согласно методу блоков восстановления, каждый программный компонент содержит тест, проверяющий его работу. Компонент имеет подпрограмму, которая повторяет вычисления, если тест обнаружил неправильное выполнение. Но повторные вычисления выполняются другой версией компонента, который построен на другой интерпретации требований, предъявляемых к компоненту. Компонент имеет несколько версий (блоков восстановления), выполняющих одинаковые функции, но реализующих разные алгоритмы [2]. Отказ такого программного обеспечения произойдет только в том случае, если в резерве компонента не останется версий, или приемочный тест пропустит ошибочный результат.

Построим модель программного обеспечения с тремя блоками (версиями) восстановления. Как и прежде R - надежность программного обеспечения,р₁,р₂,р₃ - вероятности безотказной работы версий,р_дт - вероятность безотказной работы приемочного теста, N- число версий. Сделаем следующее допущение: (1 -р_дт) есть вероятность отклонения правильного ответа.

Рассмотрим событие А - программное обеспечение работает устойчиво. СобытиеА будет выполняться, пока не откажет последняя версия, т. е. при одном из следующих условий:

• 1)    событие В - первая версия работает верно, и приемочный тест принимает результат. Вероятность этого событияр(А) =р₁р_дт;

• 2)    событие С - работает вторая версия, версия возвращает верный результат, и тест его принимает. Замена версий произойдет в случае отказа первой версии и обнаружения этого тестом (вероятность ситуации -(1-р₁)р_дт) или в случае отклонения правильного ответа,

несмотря на верное выполнение первой версии (вероятность ситуации - р₁(1-р_дт)). Вероятность события С: Р ^{( С )} = (( ^1- Р 1 )Р дт ^П^дт^ ^Р дт ;

• 3)    событие D - работает третья версия, результат верный, и он принимается. Переход к третьей версии осуществится если:

• -    откажет первая версия ^ тест обнаружит отказ ^ переход ко второй версии ^ затем откажет вторая версия ^ тест обнаружит отказ ^ переход к третьей версии, вероятность перехода - (1-р₁)р_дг(1-р₂)р_дг;

• -    откажет первая версия ^ тест обнаружит отказ ^ переход ко второй версии ^ вторая версия вернет верный ответ ^ тест отклонит верный результат ^ переход к третьей версии, вероятность перехода - (1-р₁)р_дГJр₁(1-р_дг);

• -    первая версия возвращает верный результат ^ тест отклоняет ответ ^ переход ко второй версии ^ отказ второй версии ^ тест обнаруживает отказ ^ переход к третьей версии, вероятность перехода -р₁(1-р_дт)(1-р₂)р_дт;

• -    первая версия возвращает верный результат ^ тест отклоняет ответ ^ переход ко второй версии ^ вторая версия возвращает верный ответ ^ тест отклоняет ответ ^ переход к третьей версии, вероятность перехода -ЛО^дтН^1-^).

Вероятность события D:

Р(^{D )} = ⁽⁽1-р 1 ⁾р дт ⁽1-р 2 ⁾р дт ⁺ О-р^д-ЛО-рд^ ⁺

⁺л( ^1- р дтХ ^1-^К т ⁺л( ^1- р дМ (¹^^

Так как события В, С и D являются не совместными, то надежность программного обеспечения находится как сумма вероятностей этих событий [3]:

^R ,^{рА )} ^р(^{В )} +р(^С) ⁺ Р ^{( D}) /ОР, ⁺ «^Л^дт ⁺ +р 1 ^(1- р дтМ р дт ⁺ ((¹-р 1^ р дт (¹-р 2^ р дт ⁺ ' ⁽1р Ар д, рЛр д, ^ ' р.(1р д, ^Г/'д^/'д, + ⁺ р 1 ( ^1-р _Ах ) р 2 ^(1-р _Кт ⁾ ) р з р дт .

Проводя аналогичные рассуждения для любого N, находится обобщенная формула для надежности программного обеспечения с блоками восстановления:

N          j - 1

^R = £ P j P AT П ( С ¹ — Pi ) Р AT ⁺ Р - С ¹ — P AT ) ) .

j = 1              i = 1

Зависимость надежности ПО от надежности его версий и приемочного теста представлена на рис. 3, при ус-ловиях^=3,p1=p2=p3=p.

График изменения надежности ПО с увеличением числа версий при тех же условиях что и для NVP (рис. 2) представлен на рис. 4. Надежность программного обеспечения с блоками восстановления выше по сравнению сNVP. Максимальный уровень надежности достигается уже при трех версиях по сравнению с семью для NVP. Дальнейшее увеличение числа версий не приводит к повышению надежности, это происходит из-за приемочного теста, который ограничивает надежность ПО. Изменение надежности может произойти только при изменении вероятности безотказной работы версий или теста.

Таким образом, если характеристики версий компонентом программного обеспечения заданы в виде вероятностей безотказной работы и являются постоянными на всем протяжении работы ПО, то для проектирования отказоустойчивого программного обеспечения эффективней использовать RB метод по сравнению с NVP. Во-первых, RB требует меньше версий, следовательно, сто- имость ПО будет ниже. И, во-вторых, требования, предъявляемые к приемочному тесту, а именно тест проверяет результат на приемлемость, а не само значение, гораздо ниже, чем к алгоритму голосования.

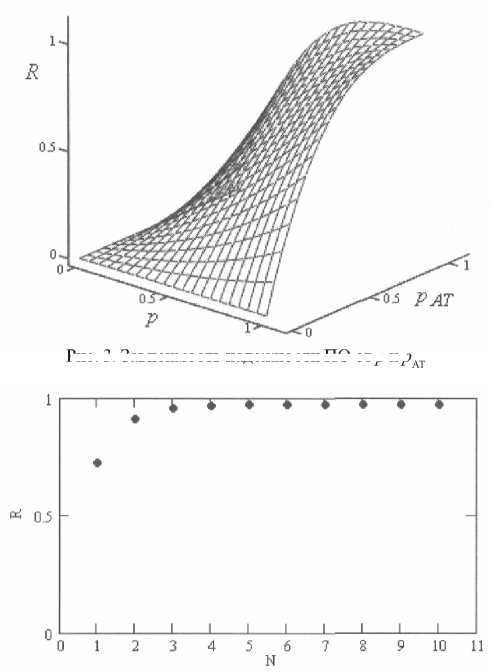
Рис. 3. Зависимость надежности ПО отрир

Рис. 4. Надежность ПО в зависимости от числа версий

Если для характеристики версий и приемочного теста используется интенсивность отказов л, то надежность программного обеспечения с блоками восстановления рассчитывается по формуле

N j — 1

R ( t ) = J e ^Ljt e ^-X AT ^t П ( ( 1 - e ""^ ) e %^t + e~'^M ( 1 - e ^;'^t ) ) , j = 1 i = 1

где %. - интенсивность отказа i версии, % _ДТ - интенсивность отказа приемочного теста.

Графики изменения надежности ПО со временем для NVP и RB метода представлены на рис. 5. Применение RB метода дает большую надежность ПО на всем интервале, кроме того, интервал времени при котором R = 1 шире, чем для NVP, что дает большую уверенность в методе блоков восстановления.

Рассмотрены два метода для проектирования отказоустойчивых архитектур программного обеспечения: N-вариантное программирование и блоки восстановления. Получены формулы для расчета надежности про граммного обеспечения с NVP и RB архитектурами. Метод блоков восстановления является эффективней, чем N-вариантное программирование независимо оттого, что является характеристикой версий вероятность безотказной работы или интенсивность отказов (см. рис. 2,4и 5).

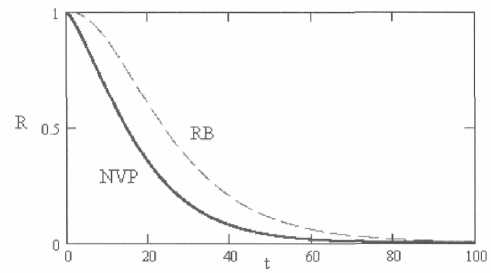
Рис. 5. Изменение надежности программного обеспечения со временем

Изменение надежности программного обеспечения происходит при изменении надежности версий, алгоритма голосования или приемочного теста и числа версий. Однако значительное увеличение числа версий не приводит к повышению надежности программного обеспечения (см. рис. 2 и 4). Это происходит из-за алгоритма голосования или приемочного теста. ДляNVP и RB метода существует оптимальное количество версий, которое даст максимальную надежность программного обеспечения. Как правило, это количество версий для метода блоков восстановления меньше, что говорит о его преимуществе.

Таким образом, при выборе метода для построения отказоустойчивой архитектуры программного обеспечения, применяемого в условиях, которые не позволят восстановить работоспособность версий, следует из N-вариантного программирования и блоков восстановления выбирать метод блоков восстановления.