Расчет натяжения прикручиваемой стренги в канале полого веретена прядильно-крутильной машины

В связи с возросшими требованиями к качеству швейных ниток актуальным в настоящее время является решение вопроса об их рациональной структуре и технологии изготовления. Установлено, что швейные нитки, вырабатываемые с применением прядильно-крутильных машин, равноценны ниткам, полученным кольцевым способом прядения не только по физико-механическим свойствам, но и по поведению их в пошиве [1]. Кроме того, производительность прядильнокрутильных машин выше производительности кольцевых прядильных машин. Поэтому использование данного способа экономически выгодно, и он является наиболее перспективным для производства комбинированных швейных ниток.

Для производства швейных ниток разработан новый процесс формирования крученых комбинированных нитей на прядильно-крутильной машине [2]. Выходящая из вытяжного прибора комбинированная нить, состоящая из комплексной нити и волокнистой оплетки, получает недостаточное число кручений при работе с нитепроводником, установленным между вытяжным прибором и полым веретеном: выше нитепроводника крутка распространяется медленно – число кручений на этом участке в 3 раза меньше, чем на участке от нитепроводника до веретена [3]. Это приводит к полной или частичной потере волокнистой мычки, которая уходит в мычкоуловитель, не успев закрепиться круткой на стержневой комплексной нити. Поэтому при формировании комбинированных нитей на машине ПК-100М3 следует работать без нитепроводника: при этом крутка быстрее распространяется до переднего цилиндра вытяжного прибора, закрепляя тем самым мычку на комплексной нити. Однако натяжение прикручиваемой стренги становится неравномерным, так как стращивание двух стренг происходит внутри канала на разной высоте от вершины веретена в зависимости от угла поворота веретена с початком, а натяжение выпрядаемой стренги значительно возрастает [3]. С целью предотвращения обрывности формируемых на полых веретенах прядильно-крутильной машины крученых комбинированных нитей необходимо получить математическую зависимость, позволяющую рассчитывать их натяжение на выходе из полого веретена при различных технологических параметрах работы машины.

Натяжение прикручиваемой стренги в канале веретена F 2ПР (рисунок 1) будет создаваться за счет сил трения нити о верхнюю часть шпинделя веретена, так как здесь происходит изменение направления ее движения. Натяжение нити со стороны баллона F 1ПР направлено по касательной N к баллону в месте входа нити в канал веретена, наклоненной к вертикали под углом α max . Натяжения F 1ПР и F 2ПР связаны формулой Эйлера [4]:

^F2nn = F inn "  ехр ( ^M ' ^вПР ) , ⁽¹ )

где д - коэффициент трения нити о верхнюю часть шпинделя веретена;

в ПР - угол обхвата нитью верхней части шпинделя веретена, рад.

Установлено, что натяжение нити со стороны баллона F 1ПР в месте входа ее в канал веретена определяется по формуле [5]:

Finn =

T ■ 10 -4 w 2L2 Г

1 + 2S-L L

■ 1,08,

где T – линейная плотность недеформированной нити, текс;

L – высота баллона, м;

S – длина баллонирующей нити, м.

Для определения угла обхвата р_ВП рассмотрим движение нити по верхней части шпинделя веретена. Введем систему координат Оxyz. Ось Оz направим вдоль оси веретена.

В точке А нить совершает продольное движение со скоростью v 1 , равной скорости вращения оттяжных валиков, и вращательное движение со скоростью v 2 :

v 2 = ω·R ВР ,                                         (3)

где R ВР – радиус вращения (расстояние от оси Оz до точки А, рисунок 1, сечение I-I), м;

го - угловая скорость вращения нити (веретена), с^-1.

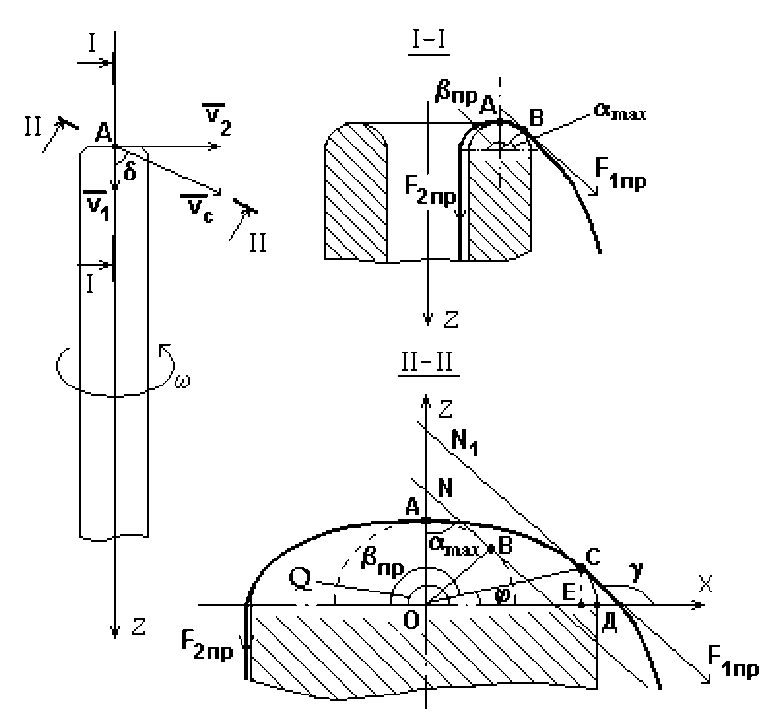
Рисунок 1 – Движение нити по верхней части шпинделя полого веретена

Суммарная скорость v С нити в точке А равна

V с = V ^V1 + v 2 = 7 v 1 + ^ш2 • R B2P ■                         (4)

Когда инерция нити не оказывает большого влияния (v2 « 0), то движение нити можно считать квазистационарным и определять ее положение на рабочих органах исходя из равновесия сил, которые существовали бы при стационарном движении (vС= v1) [6]. В этом случае положение нити на верхней части шпинделя веретена можно рассматривать в сечении I-I (рисунок 1). Угол обхвата вПР определяется как впР = П - amax■                                    (5)

Однако, ввиду того, что при формировании крученой нити на полом веретене прикручиваемая стренга совершает движение с большой скоростью (в 9,5 раз превышающей продольную), пренебрегать инерцией нити нельзя. Тогда положение нити следует рассматривать в сечении II-II (рисунок 1).

Проведем параллельно касательной N к баллонирующей нити в месте входа нити в канал веретена прямую N 1 , касательную к образовавшемуся в сечении эллипсу в точке С . Тогда угол обхвата нитью верхней части шпинделя веретена увеличится и будет равен

β_ПР = π - φ.                                       (6)

Для нахождения величины угла φ определим координаты точки С .

Уравнение касательной к линии y = f(x) в точке С ( х 0 ;у 0 ) имеет вид [7]:

у - у 0 = f'(х 0 )(х-х 0 ).                                    (7)

Каноническое уравнение эллипса записывается следующим образом [7]:

х2 у2

--1--— /

2       2       , с2 r2

где с = ОД - большая полуось эллипса, м;

r = ОА - малая полуось эллипса (рисунок 1, сечение II-II), м. После преобразований формулы (8) получили:

у = - с ² - х ² . с

Тогда

.    , ( r г-₂ ----г)       r      x₀

^f(x o ) = У о =|-V ^{е -} x o I =—-■ / ,    ,

I ^c         ) c Cc² - X 2

Кроме того, необходимо отметить, что f (x) = tgY _ tg^П + amax ) = -ctgamax .

Приравнивая правые части уравнений (10) и (11), имеем:

r      x 0

---

c² -

= ^_- ctga max . x₀²

После преобразований получаем:

е² ■ ctga_тах

^x                          i нал

⁰ л]с² ■ ^Ctg^2a max + ^r 2

.

Подставив уравнение (12) в уравнение (8), имеем:

_ r²

^У0      с² ■ ^C tg 2^am _a x + ^r2

.

Из треугольника ОСЕ, используя формулы (13) и (14) находим угол ф :

CE y r ² tg ф _ --_ — _ —₉------

OE x o c ■ ctg^a max

.

Тогда

r2

ф _ arctg----- ^c ■ ctga max

.

Малая полуось эллипса r = ОА - это радиус кривизны верхней части шпинделя веретена. Величину большой полуоси с = ОД можно определить из соотношения

r cos6 _ —.                                  (17)

c

Однако cos6 есть не что иное, как направляющий косинус суммарной скорости (рисунок 1):

cos6 _ v¹- . v_С

Из выражений (17) и (18) получаем:

r ■ vc с _---С.

v 1

Учитывая выражения (6), (16) и (19), можно определить угол обхвата нитью верхней части шпинделя веретена:

β ПР

= п - arctg

v 1²

v2 • cgmax

Как отмечалось ранее, при работе без нитепроводника стращивание двух стренг происходит внутри канала полого веретена на разной высоте от вершины веретена. Переменный угол встречи стренг в зависимости от угла поворота веретена с початком вызывает изменение угла охвата нитью верхней части шпинделя веретена. Угол обхвата β ПР , определяемый по формуле (20), является максимально возможным. Минимальный угол β ПР , когда стренги стращиваются под углом 90^о, будет рассчитываться по формуле

βПР

π

- arctg

v 1²

vC • Ctgamax

В общем виде выражение для определения угла обхвата нитью верхней части шпинделя веретена запишем как

v2

впр = Q - arctg     (-----,                   (22)

vC • Ctgamax где Q – угол, который изменяется в пределах от π/2 до π.

Используя уравнения (1), (4) и (22), получаем формулу для определения натяжения прикручиваемой стренги в канале веретена:

F 2nn = F inn

^ f                      V2

• exx p Q - arctg-^---5—----

^(        y (v2 + w2 • R2Bp)• ctga,

На рисунке 2 изображен график изменения натяжения прикручиваемой стренги в канале полого веретена при сматывании ее с разных участков початка и при стращивании стренг под различным углом.

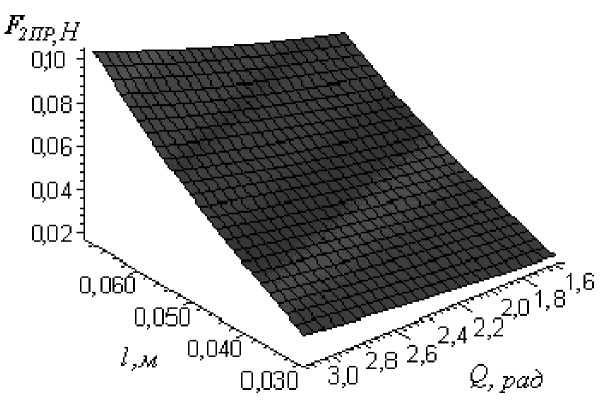
Рисунок 2 – График зависимости натяжения прикручиваемой стренги в канале полого веретена F 2ПР от высоты полубаллона l и угла Q

Как видно из графика, натяжение прикручиваемой полиэфирной армированной нити в канале полого веретена возрастает с 0,02 Н до 0,10 Н с увеличением высоты полубаллона l и угла Q .

ВЫВОДЫ

• 1.    В результате теоретических исследований получена формула, позволяющая определить натяжение прикручиваемой стренги в канале полого веретена прядильно-крутильной машины.

• 2.    Необходимо продолжить исследования процесса формирования крученых комбинированных нитей на прядильно-крутильной машине и получить формулу, позволяющую рассчитать их натяжение на выходе из полого веретена при различных технологических параметрах работы машины.