Расчет несущей способности совмещенных конических опор качения водила планетарно-цевочной передачи типа 2K-V

Введение. С начала прошлого века за рубежом в приводах различных промышленных объектов получили признание и широкое применение планетарно-цевочные передачи с внецентроидным внутренним цевочным зацеплением, выполненные по схеме К-Н-V, c неподвижным цевочным колесом и двумя параллельно работающими эпициклоидными сателлитами. Дальнейшее развитие эти планетарные передачи получили в редукторах фирмы «Sier Bath», в которых к передаче K-Н-V была добавлена эвольвентная планетарная ступень с ведущей центральной шестерней [1]. Эвольвентные сателлиты в ней располагались на валах параллельных кривошипов, а водило являлось выходным звеном. По предложению В.Н. Кудрявцева этой передаче присвоено условное обозначение 2K-V. Отличительной особенностью передачи 2K-V является высокая степень упаковки всех деталей, компактность, наличие самоторможения и возможность реализации передаточного отношения от 20 до 500 в одной ступени. В настоящее время эти передачи широко применяются в приводах звеньев промышленных роботов (например, антропоморфные сварочные роботы фирмы «Kuka»).

Наличие нескольких двухэксцентриковых валов дает возможность распределить поток мощности по нескольким направлениям, получить оптимальный вариант распределения нагрузки между эпициклоидными и эвольвентными сателлитами и уменьшить нагрузки, действующие на опорные подшипники. Наличие в данной схеме быстроходной эвольвентной ступени создает благоприятные условия для значительного увеличения передаточного отношения редуктора и также способствует улучшению режима работы подшипниковых узлов.

Однако малые габариты подобного типа редукторов, необходимость применения разнотипных подшипников качения с различной статической и динамической грузоподъемностью, увеличение их количества резко снижают, а в некоторых случаях делают даже невозможным применение в проектируемых подшипниковых узлах серийно выпускаемых стандартных подшипников качения. Это требует индивидуального подхода к выбору типа и конструкции каждого подшипникового узла, входящего в проектируемый редуктор.

Расчет несущей способности совмещенных конических опор качения водила. На рис. 1 показана кинематическая схема одного из вариантов исполнения планетарно-цевочного редуктора, выполненного по трехваловой схеме с быстроходной эвольвентной передачей 3, 1 (на схеме показаны только два эксцентриковых вала 8 из трех). Крутящий момент в данной конструкции снимается с водила 10, которое дополнительно нагружено осевой силой FН и опрокидывающим моментом Мо (рис.2), действующими со стороны исполнительного устройства. Их комплексное действие на водило, приводит к созданию радиальной и осевой нагрузки на опору 5, которые определяют ее тип и необходимую динамическую грузоподъемность. Жесткие требования к габаритам и массе редуктора в данном случае приводят к необходимости совместного изготовления внутреннего кольца подшипника и корпуса водила, а также к применению нестандартного типа конических роликов.

Рис.1. Кинематическая схема планетарного редуктора 2K-V с внецен-троидным внутренним цевочным зацеплением: 1 – колесо зубчатое эвольвентной ступени; 2 – опорный подшипник ведущего вала-шестерни; 3 – ведущий вал-шестерня; 4 – корпус редуктора; 5 – совмещенные конические опоры качения водила; 6 – эпицикло-идный сателлит; 7 – опорные подшипники эпициклоидных сателлитов; 8 – вал эксцентриковый; 9 – опорные подшипники эксцентриковых валов; 10 – водило

Все основные параметры данной опоры качения, в том числе и угол контакта конического ролика с наружным кольцом, а также точки приложения радиальной и осевой нагрузок, необходимые для расчета ее несущей способности и долговечности, могут быть определены только после детальной конструктивной проработки всех деталей редуктора и его конструктивной компоновки. В связи с этим после рекомендуемой [2] разбивки общего передаточного числа проводится полный силовой расчет быстроходной эвольвентой ступени с определением ее межосевого расстояния, окружных сил, радиальных составляющих и подбором опорного подшипника 2 ведущего вала-шестерни. Расчет быстроходной ступени выполняется по моменту, равному моменту на входе вала-шестерни.

Межосевое расстояние быстроходной ступени одновременно определяет расположение эксцентриковых валов и их опорных подшипников 9, которые совместно с эксцентриковыми валами также устанавливаются в корпусе водила. Указанные подшипники нагружены окружными и радиальными силами, возникающими в зацеплении сателлитов эвольвентной ступени с шестерней и определяющими их параметры. Размеры этих подшипников оказывают весьма значительное влияние на ширину эпициклоидных сателлитов цевочной передачи 6, а также на габариты и размеры конических радиально-упорных совмещенных опор качения водила 5 и в связи с этим должны иметь минимальные габариты.

Опорные подшипники 7, несущие эпициклоидные сателлиты 6 на эксцентриковых валах 8, по данным работы [3], являются наиболее нагруженными и их конструктивные параметры принимают в соответствии с необходимыми расчетами. По полученным размерам подшипников определяют, ширину и диаметральные размеры эпициклоидных сателлитов. Его размеры оказывают также существенное влияние на конструктивное исполнение совмещенных конических опор качения водила 5.

Перед компоновкой редуктора необходимо выполнить расчет цевочной ступени и определить все ее основные параметры [4].

Общая компоновка редуктора дает возможность предварительно определить основные параметры и угол контакта конического ролика α (рис.2), которые могут быть уточнены в ходе выполнения его силового расчета. Определяющими при этом являются, как правило, заданные техническим заданием габариты корпуса редуктора, размеры водила и расположение относительно оси его вращения конических роликов, полученное при компоновке. Задают диаметр большего торца конического ролика и его длину. При этом учитывают характер и уровень действующих на опору сил, необходимость обеспечить достаточные геометрические параметры наружного кольца совмещенной опоры по условиям технологической жесткости и прочностным характеристикам, а также возможность исполнения беговых дорожек в теле водила, выполняющих роль внутренних колец совмещенных опор качения.

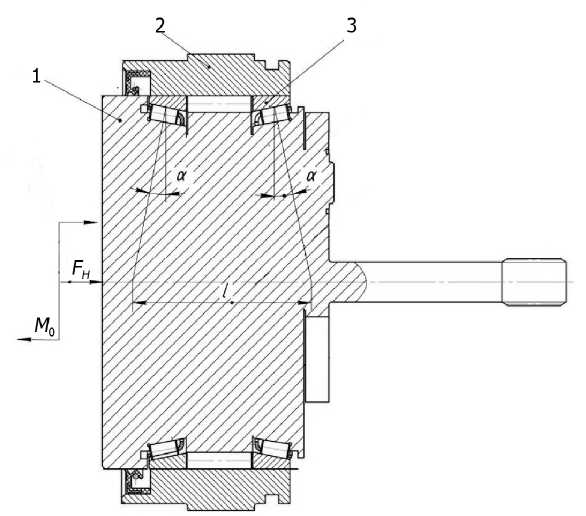
Рис.2. Общая компоновка совмещенных конических опор качения водила планетарноцевочного редуктора 2K-V: 1 – водило в сборе с комплектующими узлами и деталями; 2 – корпус редуктора; 3 – совмещенная коническая опора качения водила; α – угол контакта конического ролика; М _о – опрокидывающий момент; F_H – внешняя осевая сила; l – расстояние между точками приложения опорных реакций

Затем на оси вращения водила определяют точки приложения опорных реакций и расстояние l между ними (рис.2). С учетом полученных размеров, строят схему нагружения совмещенных конических опор качения водила (рис.3) и рассчитывают радиальные и осевые нагрузки, действующие в опорных узлах.

Значения показанных на расчетной схеме радиальных сил, действующих в опорах от опрокидывающего момента, определяют по формуле:

M о

F _rA = F _rБ = _l .

где F rA и F rБ – радиальные опорные реакции, действующие в опорах.

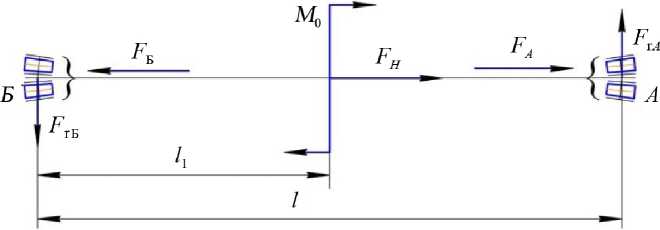
Рис. 3. Схема действия сил в опорных узлах водила

Дополнительные осевые составляющие F А и F Б зависят от радиальных сил F rА и F rБ и коэффициента осевого нагружения е и для конических радиально-упорных подшипников могут быть определены по зависимостям [5]:

e = 1,5tg a ;      F = 0,83 eF rA ; F^ = 0,83 eF ^.

С учетом действия осевой силы F Н максимальным для данной схемы нагружения будет усилие в опоре А, которое выражается как

F А = F А + F Н = 0,83 eF rA + F Н .

Базовая динамическая радиальная грузоподъемность для каждой из совмещенных радиально-упорных конических опор качения водила может быть определена по зависимости [5]:

Cr = bm f c (iLw. cosaf Z3/4DW^27, где Cr – базовая динамическая радиальная грузоподъемность, Н; bm – коэффициент, характеризующий свойства стали с учетом способа ее изготовления (для конических роликов bm=1,1); fc – коэффициент, зависящий от геометрии деталей подшипника, точности их изготовления и материала; i – число рядов роликов в подшипнике; LWe – длина ролика для расчета грузоподъемности, мм; Z – число роликов в однорядном подшипнике; DWe – диаметр ролика, мм.

Коэффициент f c определяется по табличным данным в зависимости от отношения

Dw cos a e [5], где D – диаметр окружности центров комплекта роликов, мм. Например, при

^D p W               ^{p W}

D_w cos a значении отношения ^e , D _{p W}

равном 0,0438 для разработанного варианта планетарной пере- дачи 2K-V с внецентроидным внутренним цевочным зацеплением, имеющего обозначение ПЦР 3–36(6), коэффициент fc составляет 64,09.

Динамическая эквивалентная радиальная нагрузка для наиболее нагруженной опоры А при α ≠0 определяется по формуле [5]:

P = (ХVFr + YFА)KбKт, где P – эквивалентная радиальная нагрузка, Н; X и Y – коэффициенты радиальной и осевой нагрузки. Если Fa/(VFr)<е, тоX=1, Y=0; если Fa/(VFr)>e, то X=0,4, Y=0,4ctga; V- коэффициент вращения; Fr – радиальная нагрузка и FA – максимальная осевая нагрузка, действующие на опору А, Н; Kб – коэффициент безопасности, принимаемый при умеренных перегрузках до 150% от 1,3 до 1,8; Kт – температурный коэффициент, принимаемый при температуре до 100 °С равным 1.

Полученные значения динамической грузоподъемности С и эквивалентной радиальной нагрузки P используют для определения ресурса подшипника [5]:

_ 10 6 (

60 n (

C P где Lh – долговечность подшипника, ч; n – частота вращения водила, мин–1.

Заключение. Получаемое значение долговечности рассматриваемого подшипника сравнивают с требуемой и, в случае несоответствия, уточняют параметры конического ролика и угол контакта α с последующим повторением силового расчета и определением ресурса работы подшипника с уточненными параметрами. По подобной методике могут быть определены параметры и других совмещенных опор качения, установка в которых стандартных подшипников по тем или иным причинам оказывается невозможной.