Расчет неустановившихся электромагнитных полей в линиях передачи

Электронные и радиоэлектронные компоненты и системы подвержены воздействию внешних электромагнитных полей. Одним из наиболее мощных источников электромагнитных полей естественного происхождения является грозовой разряд. Испытания электронных и радиоэлектронных систем на устойчивость к электромагнитным полям большой интенсивности могут проводиться как в полевых условиях, так и при использовании экранированных камер. Наиболее часто для этих целей используют экранированную Т-камеру [1,2,3]. Такая камера в большинстве случаев представляет собой регулярную симметричную полосковую линию с геометрическими размерами, которые обеспечивают требуемую неравномерность электромагнитного поля в пределах исследуемого устройства [4]. На входе и выходе регулярной части Т-камеры включены согласующие переходы, к которым подключены импульсный источник сигнала и согласованная с Т-ка-мерой нагрузка. Представляет интерес рассмотрение явлений в Т-камере, возникающих при имитации грозового разряда.

Решить задачу определения пространственновременной зависимости электромагнитного поля внутри Т-камеры с учетом согласующих переходов строгим электродинамическим методом при произвольной форме возбуждающего сигнала не представляется возможным. Это обусловлено тем, что в Т-камере могут распространяться одновременно несколько типов волн. Кроме того, распространяющиеся по камере волны частично отражаются от нерегулярных участков и от нагрузки, включенной на конце камеры. Эти отраженные волны также изменяют распределение поля в регулярной части Т-камеры.

Рассмотрим вначале пространственно-временное распределение поля в регулярной части Т-камеры, а затем определим влияние отражений от нерегулярностей, а также влияние рассогласования генератора и нагрузки с Т-камерой на распределение поля внутри нее.

Электромагнитные поля в регулярных однородных линиях передачи без потерь, описывающие переходные процессы и последующий установившийся режим, имеют сложную пространственно-временную структуру. Рассмотрим существующие методики расчета электромагнитных волн внутри регулярной линии передачи при произвольной форме возбуждающего сигнала. В настоящее время наиболее часто при решении подобных задач используют два подхода.

Первый подход основан на применении прямого и обратного преобразований Лапласа, т.е. на представлении произвольно изменяющегося во времени возбуждающегося сигнала в виде непрерывного спектра [5,6]. Такой подход во многих случаях не является оптимальным. Стационарные гармонические во времени волны отличны от нуля во всей области изменения пространственных переменных. В это же время их суперпозиция, соответствующая преобразованию Лапласа, должна привести к описанию волнового процесса, отличного от нуля в определенные моменты времени, заданные источником. Вследствие этого для адекватного описания нестационарного процесса требуется учет большого числа гармоник. Поэтому решения, полученные таким методом, как правило, громоздки, и они не отображают во многих случаях физические явления в рассматриваемой структуре. Если же рассматриваемая структура является многомодовой, то задача еще более усложняется.

Второй подход основан на решении уравнений Максвелла, в которых задана временная зависимость сторонних источников [7]. При таком подходе в ряде случаев получаются более простые решения. Методика построения решения нестационарных задач, в которых искомое решение - электромагнитное поле - представляется в виде пространственно-временной зависимости, сводится к следующей последовательности:

• 1.    Систему уравнений Максвелла преобразуют таким образом, чтобы получилось уравнение второго порядка в частных производных для составляющих векторов электромагнитного поля или векторного потенциала.

• 2.    При решении полученного уравнения используется метод неполного разделения переменных, при котором исходное дифференциальное уравнение сводится к системе обыкновенных дифференциальных уравнений. Одно из этих уравнений зависит от двух, как правило, поперечных координат, а другое - от продольной координаты и времени.

• 3.    Решается уравнение, зависящее от двух пространственных координат, совместно с граничными условиями.

• 4.    Решается уравнение, зависящее от времени и одной пространственной координаты.

Применим эти подходы к определению пространственно-временных характеристик продольнорегулярной линии передачи при произвольном законе изменения во времени возбуждающего сигнала.

1. Возбуждение продольно-регулярной линии передачи сторонним источником электрического тока

Электромагнитное поле в регулярной линии передачи при произвольном законе изменения во времени стороннего источника определяется уравнениями Максвелла, начальными и граничными условиями. Будем считать, что линия передачи возбуждается сторонним источником электрического тока.

Нестационарное (неустановившееся) электромагнитное поле описывается системой уравнений Максвелла, которую для рассматриваемой структуры (рис.1) можно записать в виде:

вия. Считая проводники идеально проводящими, граничные условия для касательной составляющей — электрического ET и нормальной составляющей

— магнитного Hn полей можно записать в виде:

E . I s = 0- H . I s = 0,

где S - идеально проводящие поверхности регулярной линии передачи.

При таких начальных и граничных условиях требуется определить пространственно-временное

распределение электромагнитного поля в рассмат-

б)

*

. —  dD , — rotH = -;- + 7Cm-dt

.—     dB

< rotE = , dt

— divD = 0, — divB = 0.

риваемой структуре.

Систему уравнений Максвелла (1) можно свести к неоднородным уравнениям Гельмгольца для

векторов электрического и магнитного полей

<

'   —        22E 01

2                           ^j ст

V E ^aMa   2   ^a д, - dt2          d t s ,— „      d2 TH             -

^V H ^- S a ^ a—T- = ^- rot j cm ^- d t ²

• (4)

• (5)

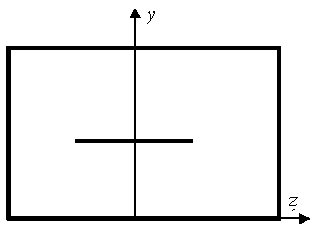
а)

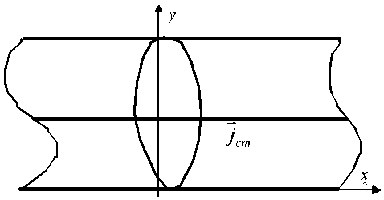
Рис.1. Поперечное (а) и продольное (б) сечения регулярной части Т-камеры

Входящие в эти уравнения электрическое E и магнитное H поля, а также сторонний источник электрического тока j_ст в общем случае зависят как

от пространственных координат, так и от времени.

Без нарушения общности будем считать, что электромагнитная волна возбуждается сторонним источником электрического тока j_ст , который включается в момент времени t =0.

При t <0 амплитуда стороннего источника рав-

на нулю, и электромагнитное поле во всех точках

внутри рассматриваемой структуры отсутствует:

E I   = 0 , H = 0 .

1 t < 0                I t < 0

В любой момент времени на поверхности регулярной линии должны выполняться граничные усло-

где ε _a , µ _a - соответственно абсолютные диэлектри-

ческая и магнитная проницаемости среды, заполняющей рассматриваемую структуру.

Полученные дифференциальные уравнения (45) - векторные. Проектируя их на декартову систему координат, получим для каждой составляющей вектора E , - H , - j _cm , ( , = x - y - z ) систему скаляр-

ных уравнений

V ² E ,

-8 Ц a^a

v ² H

d ² E § d t ²

^d 1 cm, ,

⁼ ^a "^T^- d t

^{d 2} H ,     ( л

^{- S}a^a ""бё" ⁼ -⁽ ^ст ), "

В точках пространства, где свободные источники отсутствуют, система уравнений (6) преобразуется к однородным дифференциальным уравнениям для каждой , -ой составляющей поля:

2           ^{5 2} E^

^{V 2 E} , — ^ _а Ц _а —2- = ⁰ .                        d t

^{6 2} H, [^{V 2 H}- — ^£ a ^ a "^ = ⁰ -

Решим в области, где отсутствуют сторонние источники, систему уравнений (7) методом Фурье. Решения уравнений ищем в виде:

E , ( x , y , z , t ) = E i , ( x , y ) • E 2 , ( z - 1 ) ,      (8)

H , ( x - y - z - 1 ) = H i , ( x - y ) • H 2 , ( z - 1 ) .    (9)

Применяя известную процедуру разделения переменных, получим систему дифференциальных уравнений, эквивалентную исходной системе уравнений (7):

^{v2 E} p ^{( x} , У ^{)+ v} E • ^E 1 ^ ⁽ X , у ) = ⁰

‘

d ² E 2 _p ( z , t ) d z ²

8 ² E 2 , ( z , t )

Sa ^a -------- dt2

- v E ■ E 2 ^ ( z , t ) = 0,

v 2 Hp (x, У)+ vH •Hp (x, У) = 0

8 ² H 2 ^ ( ^ , t )

d z ²

Sa ^a

8 ² H 2 _p ( z , t ) d t ²

-v H ■ H 2 ^ ( z , t ) = 0,

где V² - поперечный оператор Лапласа,

V _E , v _H - константы разделения.

Из полученных соотношений следует, что пространственно-временное распределение электрического и магнитного полей описывается соотношениями (8) и (9) соответственно. Эти соотношения представляют собой произведение двух сомножителей, один из которых описывает зависимость составляющих полей от поперечных координат E 1 , ( x , у ) , H 1 , ( x , у ) , а другой - от продольной координаты и времени E₂ , ( z , t ) , H₂ , ( z , t ) . Функции, описывающие поперечную структуру электрического E 1 , ( x , у ) и магнитного H 1 , ( x , у ) полей и константы разделения v _E и v _H , определяются из решения уравнений (10), (12) совместно с граничными условиями (3). Результатом решения этой задачи являются дискретный спектр собственных значений константы разделения v р = v _E = v _H и зависимости функций E , ) ( x , у ) , H⁽⁽ p ) ( x , у ) от поперечных координат. Индекс р , появляющийся в результате решения уравнений (10) и (12), характеризует разные законы распределения поля по поперечным координатам (различные типы волн в регулярной линии передачи). В результате этого полное поле в регулярной линии передачи определяется соотношениями

^E p ^{( x} , у , z , t ) = £ ^E 1 ⁽ р ) ^{( x} , у ) ■ ^E 2 р ) ⁽ z , t ) р                           (14)

H , ^{( x} , у , z , t ) = £ H 1 ⁽ р ) ^{( x} , у ) ■ H 2 р ) ⁽ z , t ), .

р где E 2р) (z, t), H2р) (z, t) - решения уравнений (11), (13).

Из приведенных соотношений следует, что полное поле в регулярной линии передачи состоит из суммы слагаемых, каждый член которой описывает пространственно-временное распределение волны типа p .

Амплитуды каждого p - типа волны определяются из решений неоднородных уравнений (6) с уче-

том начальных (2) и граничных (3) условий. Продольное распределение поля зависит от значения константы разделения у _p .

Те p - типы волн, для которых у _p - мнимые числа, являются затухающими. Затухающие поля локализованы вблизи источника, влияют только на согласование источника стороннего тока с линией передачи и в передаче энергии не участвуют.

Те p - типы волн, для которых у _p - вещественные числа, являются распространяющимися. Такими распространяющимися волнами являются основная Т-волна симметричной полосковой линии, а также высшие типы волн симметричной полосковой линии, которые могут возбуждаться только при определенных условиях [8]. Ограничимся учетом только одной основной моды.

В силу того, что в рассматриваемой структуре (рис.1) отсутствует диэлектрическое заполнение, основная Т-волна является бездисперсной и имеет фазовую скорость, равную скорости света.

Поэтому возбужденный в начале структуры импульс распространяется вдоль регулярной линии передачи без искажений. Эта особенность позволяет существенно упростить анализ переходных процессов в регулярной линии.

2. Расчет переходных процессов в Т-камере с учетом отраженных волн

Представим регулярную часть Т-камеры в виде эквивалентной линии [6]. Такая эквивалентная линия передачи по ряду электродинамических параметров будет идентична регулярной части Т-камеры, если в обеих линиях распространяется только один тип волны, равны их волновые сопротивления и постоянные распространения у _p .

Фазы распределения напряжения в эквивалентной линии u ( t ) совпадают с фазами поперечной составляющей электрического поля регулярной части Т-камеры, а напряжение u ( t ) и ток i ( t ) в ней пропорциональны напряженностям поперечных составляющих соответственно электрического и магнитного полей основного Т-типа волны симметричной полосковой линии [4]. Пренебрежем влиянием нерегулярностей, обусловленных соединением конусных переходов с регулярной частью Т-камеры. Тогда их также можно считать отрезками регулярной линии передачи (радиальной линии) и заменить отрезками эквивалентных линий. Это позволяет проанализировать характеристики не только регулярной части, но и всей Т-камеры.

Рассмотрим переходные процессы в Т-камере, если на ее входе включен генератор с заданной формой импульсного напряжения u ( t ) и внутренним сопротивлением Z_r , а на выходе - в общем случае произвольная нагрузка Z н .

Вначале проанализируем переходные процессы при наиболее простом скачкообразном воздействии на входе Т-камеры (рис.2):

u ( t ) = U m - 1 ( t ) ,

где U_m - амплитуда напряжения, пропорциональная

амплитуде поперечной составляющей электрического поля основной Т-волны,

1 ( t ) -единичная функция Хевисайда,

1 ( t ) [ 0, если t <  0,

1 1, если t >  1.

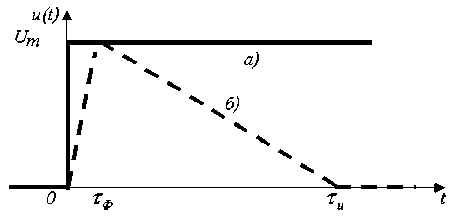
Рис.2.Скачкообразное (a) и пилообразное (б) воздействия на входе Т-камеры

где U ( z , p ), I ( z , p ) - операторное изображение соответственно напряжения u ( t ) и тока i ( t ) в эквивалентной линии,

Y - комплексная постоянная распространения основной волны.

Решение этой системы уравнений определяется соотношениями

\ U ( z , p ) = U n ( p ) • e ^{- i Y} z + U о ( p ) • . ,         ⁽¹⁶⁾

1 ¹ ^p ’ = Z ( p ) ( U n ⁽ p - U 0 ⁽ p ’ ' e *) (17) где Z ( p ) - операторное выражение волнового сопро-

тивления,

U_n ( p ) , U ₀ ( p ) - постоянные, определяемые гранич-

ными условиями.

Если пренебречь активными потерями в Т-камере, то Z ( p ) = Z в . Находя оригиналы изображений (16), (17) и используя граничное условие на

Распространяющуюся основную моду, амплитуда которой зависит от времени (входное воздействие), представим в виде интеграла Фурье:

U ( t ) = U m • 1 ( t ) = U m •

f ¹ +

v

1 г Sin tot , — -----dto n 0 to

концах линии, получим выражение для напряжения u ( z , t ) и тока i ( z , t ) в любой точке линии z в произвольный момент времени t при скачкообразном входном воздействии u ( t ) = U m ■ 1( t ):

При отсутствии активных потерь фазовая скорость V в линии передачи от частоты не зависит и она равна скорости света. Поэтому все гармонические составляющие входного воздействия распространяются без затухания и с одинаковой фазовой

u ( z , t ) 1

| U m i ^{( z} , t ’ • ^z в J

±Г н -1l t —

2 1 — x

V

+ Г2Г -1| t-нг

скоростью, и напряжение в момент времени t в произвольной точке z равно [5]

u ⁽ z , t ) = U m '

f

1 +

I

„ Sin to l t I

17    v

П 0

I¹ d to

v

Из этого соотношения следует, что входное воздействие распространяется по линии передачи без искажения. Это справедливо и для входного воздействия произвольной формы.

Проанализируем влияние сопротивления нагрузки Z_н и генератора Z_г на переходные процессы в Т-камере при скачкообразном изменении входного воздействия, временная зависимость которого описывается соотношением (15).

Все процессы в эквивалентной линии передачи с распределенными параметрами описываются системой уравнений, которая в операторной форме имеет вид [6]:

d 2 U (Z, p’ + Y2 U (z, p ) = 0, dz d '( p’) + y 21 (z, p ) = 0, dt

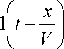
Л I      2 1 + x I

+ Г г • 1| t--1 ± н г I у 1

4 1 — x

V

+Г2 ГM

±Г 3 г²- 1 ^f t — 6 l—x | + ^н г v у )

33 нг

t

6 1 + x |± у )

Здесь Г _н , Г _г - комплексные коэффициенты отражения по напряжению соответственно от нагрузки и генератора.

На рис.3 в качестве иллюстрации описанной выше методики приведены рассчитанные по соотношению (18) временные зависимости нормированных напряжения (а) и тока (б) в эквивалентной линии при Г _н = Г _г = 0.5. Из приведенных зависимостей следует, что время установления электромагнитного поля в центре Т-камеры при указанных выше параметрах составляет величину не более 0,6мкс. По мере согласования нагрузки и генератора с Т-камерой длительность установления электромагнитного поля уменьшается.

Представляет интерес проанализировать влияние согласования генератора и нагрузки с Т-камерой на временные зависимости электромагнитного поля при входном воздействии в виде пилообразного импульса напряжения, имитирующего грозовой разряд. Пусть воздействие на входе Т-камеры описывается соотношением (рис.3)

при t <  0,

t

u„ „ ( t ) = U« вх        m

^Т Ф

1 -

t- тф ти -тф

при 0 < t < Тф, при тф < t < ти ,

t

~ ( z , t ) = J u ( z , t - T ) • u вх ( т ) d т ,

t i (z, t ) = JI (z, t - T )• uBх (T )• ze • dT ,

где u ( z , t ) и i ( z , t ) определяются выражениями (18).

пРи ^т и <  t .

Здесь Т ф - длительность переднего фронта импульса грозового разряда, Т ф =1,2мкс, т и - длительность импульса грозового разряда, т и =50мкс.

Искомые временные зависимости напряжения ~ ( z , t ) и тока i ( z , t ) в эквивалентной линии передачи можно определить с помощью соотношений

а)

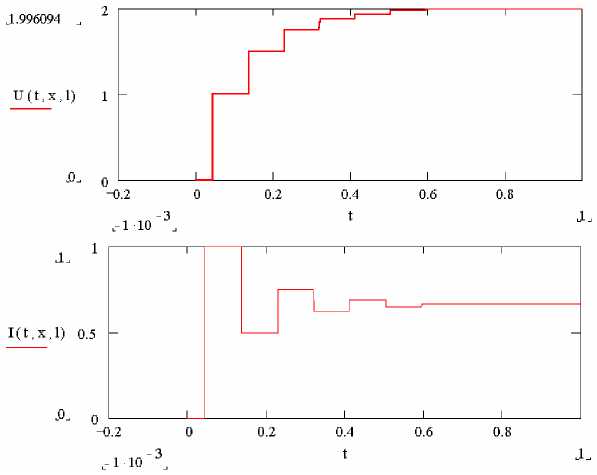
б)

Рис.3.Временные зависимости нормированных напряжения (а) и тока (б) в эквивалентной линии в различные

моменты времени t при

На рис.4 приведены в качестве примера рассчитанные по соотношениям (20), (21) временные зависимости нормированных напряжения и тока при Г г = Г н = 0.5 в середине Т-камеры. Из представленных зависимостей следует, что при указанных выше коэффициентах отражения временные зависимости напряжения и тока в Т-камере отличаются от входного сигнала незначительно, что обусловлено малой длительностью переходного процесса установления колебаний в ней.

г - г нг

Заключение

Рассмотрена методика расчета электрического и магнитного полей в регулярной части Т-камеры при произвольном возбуждающем сигнале.

Получены аналитические выражения, позволяющие проанализировать переходные процессы в эквивалентной линии передачи при произвольной форме возбуждающего сигнала.

Рассчитаны переходные процессы в эквивалентной линии передачи при скачкообразном измене-

= 0.5 (Время в t мкс)

нии входного воздействия. Показано, что длительность переходных процессов определяется величинами коэффициентов отражения от нагрузки Г _н и генератора Г г . В частности, при Г г = Г _н =0.5 длительность переходных процессов составляет 0.5…0.6 мкс, и она будет уменьшаться по мере согласования нагрузки и генератора с Т-камерой.

Рассчитан переходный процесс установления электромагнитного поля в Т-камере при пилообразном изменении входного сигнала, имитирующем электрическое поле грозового разряда.

Приведенные аналитические выражения позволяют рассчитать переходный процесс установления электромагнитного поля в Т-камере при произвольном законе изменения входного сигнала и произвольных сопротивлениях генератора и нагрузки и определить тем самым необходимый частотный диапазон и допустимую неравномерность частотной характеристики КСВ нагрузки.

б)

•

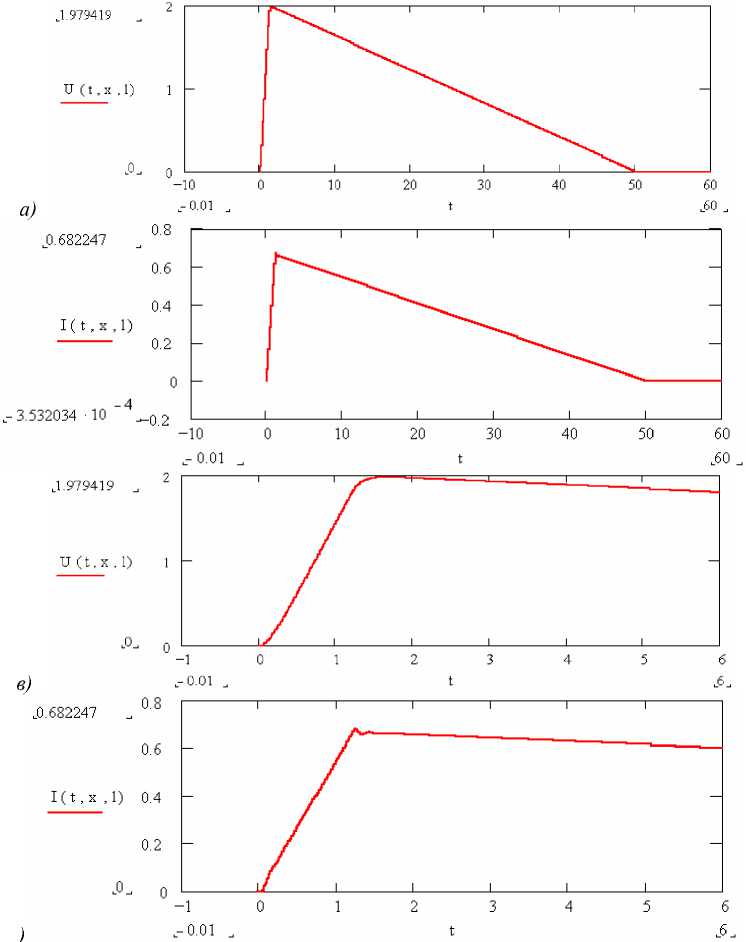
г)

Рис.4.Временные зависимости нормированных напряжения (а), (в) и тока (б), (г) в эквивалентной линии при пилообразном изменении напряжения и Гг = Гн = 0.5 (Время в t мкс)