Расчет нормативов контроля для определения антибиотиков в лекарственных препаратах

Антибиотики различной химической природы широко применяются в медицинской практике в качестве антимикробных препаратов для лечения инфекционных заболеваний. Контроль качества этих препаратов, а также необходимость учета протекания побочных химических реакций антибиотиков в организме в силу их высокой реакционной способности обусловливают актуальность разработки методик их количественного определения.

Весьма привлекательны с точки зрения простоты выполнения, экспрессности, доступности оборудования электрохимические и фотометрические методы, которые могут быть применены в количественном анализе пенициллинов (β-лактамных) антибиотиков. Последние являются, с одной стороны, органическими кислотами, с другой – органическими биолигандами, т.к. в их структуру входят электронодонорные группы различной природы (С(О)ОН, С(О)NH, R-S-R, NH 2 ) и, следовательно, эти реагенты потенциально способны к образованию донорно-акцепторных связей с катионами металлов, в частности с d -элементами, с ионами меди. Склонность меди к образованию комплексных соединений объясняется ее электронной конфигурацией ( 3d⁹) , что делает ион меди (II) легко деформирующимся, благодаря чему он образует прочные донорно-акцепторные связи с донорными группами лигандов, особенно группами, содержащими согласно теории Сиджвика, гетероатомы азота, кислорода и серы.

Как показано в обзоре [1], данные по комплексообразованию антибиотиков с катионами меди (II) разнятся как по составу и устойчивости комплексов, так и по оптимальным условиям их образования. Авторами [2-4] изучено комплексообразование меди (II) с β-лактамными антибиотиками потенциометрическим и спектрофотометрическим методами и указано на возможность аналитического применения данной реакции. Но в методике отсутствует завершающая стадия – оценка результатов анализа по нормативам контроля из-за отсутствия последних. В связи с этим цель нашей работы – рассмотреть взаимодействие меди с некоторыми пенициллинами, рассчитать метрологические характеристики спектрофотометрического определения пенициллинов с использованием реакции их комплексообразования с катионами меди и назначить нормативы оперативного контроля.

Экспериментальная часть

В работе использовали динатриевую соль бензилпенициллина («Биосинтез», Пенза), натриевую соль ампициллина («Красфарма», Красноярск), тригидрат ампициллина («Биосинтез», Пенза), тригидрат амоксициллина («Барнаульский завод медицинских препаратов», Барнаул). Предварительный анализ препаратов, проведенный по методикам фармакопейных статей, показал, что содержание основного вещества составляет не менее 99,5%. Субстанция ампициллина с содержанием основного вещества – 99,9%. Раствор соляной кислоты (С=0,05 моль/л) готовили из фиксанала. Для приготовления 0,05 моль/л раствора гидроксида натрия использовали препарат марки ч.д.а. Исходный раствор Cu(NO 3 ) 2 с концентрацией 2·10^-2 моль/дм³ готовили из навески соли квалификации х.ч. Стандартизацию растворов гидроксида натрия и нитрата меди (II) проводили кислотно-основным и комплексонометрическим титрованием соответственно. Постоянная ионная сила создавалась с помощью раствора KCl c концентрацией 0,1 моль/л. Все растворы готовили на дистиллированной воде.

Для измерения рН использовали иономер «Эксперт-001» со стеклянным электродом. Калибровка иономера осуществлялась по буферным растворам с pH 1,68, рН 3,56, рН 4,01, pH6,86, pH 9,18. Точность измерения рН ±0,02. Все растворы для потенциометрических измерений термостатировали при температуре 20оС. Измерение оптической плотности проводили на КФК-3-01 в кварцевых кюветах. Использовали высокоэффективный жидкостный хроматограф "Милихром А-02" (ЗАО "ЭкоНова", Новосибирск).

Кислотно - основные свойства бензилпенициллина, ампициллина, амоксициллина

Кислотный характер пенициллинов обусловлен наличием в их структуре карбоксильной группы. Аминогруппа ампициллина и амоксициллина придает им амфотерный характер. Амидная, лактамная и тиазолидиновая группы не обладают выраженными кислотно-основными свойствами, т.е. бензилпенициллин является одноосновной карбоновой кислотой, ампициллин – одноосновной аминокислотой, амоксциллин – одноосновной оксиаминокарбоновой кислотой.

Константы кислотной диссоциации антибиотиков определяли титриметрическим методом с использованием графического варианта метода Бьеррума, предусматривающего расчет функций образования и построение кривых образования (рис. 1-4).

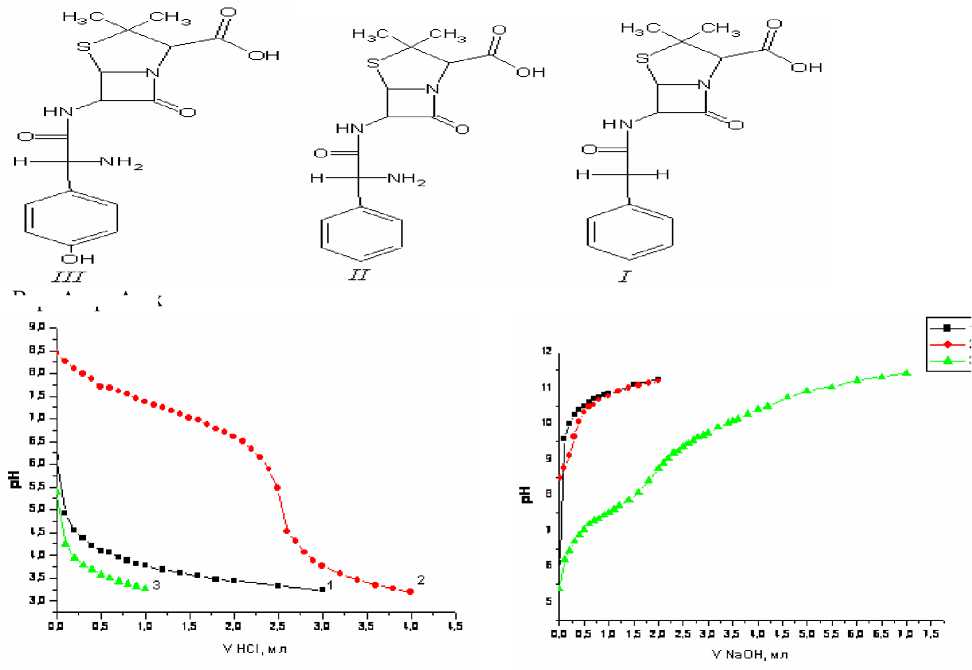
Bzp Amp Amx

Рис. 1. Кривые рН-метрического титрования растворов: 1 – 2.8·10-3 M NaBzp, 2 – 2.7·10-3 M NaAmp, 3 – 2.5·10-3M HAmx. Титрант 0.05 М HCl, µ = 0.1 (KCl)

Рис. 2. Кривые рН-метрического титрования растворов: 1 – 2.8·10-3 M NaBzp, 2 – 2.7·10-3 M NaAmp, 3 – 2.5·10-3M HAmx.Титрант – 0.05 М NaOH, µ = 0.1 (KCl)

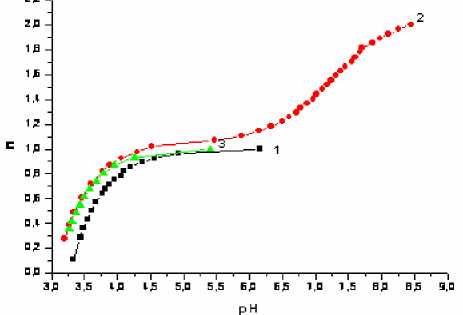
Рис. 3. Кривые образования Bzp (1), Amp (2), Amx (3)

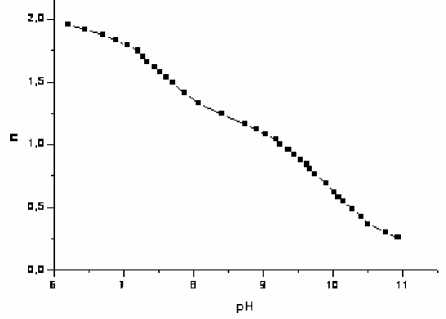
Рис. 4. Кривая образования Amx

Сопоставление рК а пенициллинов (табл. 1) со значениями рК а карбоксильных групп оксикарбоновых кислот [5] показывает, что антибиотики близки по силе к оксикислотам, но сильнее алифатических кислот (уксусной, пропионовой, масляной, валериановой), т.е. проявляется влияние индуктивного эффекта гетероатомов и мезомерного эффекта, обусловленного наличием гетероатомов с непо-деленными электронными парами и систем с двойными связями.

Ампициллин и амоксициллин близки по кислотно-основным свойствам к аминокислотам, но основность их аминогрупп ниже, чем у аминокислот: для глицина рК а 9,78, для аланина – 9,87 [5]. Повышение основности аминогруппы амоксициллина по сравнению с основностью аминогруппы ампициллина связано с влиянием фенольной группы.

В свою очередь кислотность фенольной группы амоксициллина ниже, чем у фенола (рК а 9,90) и сопоставима с аналогичным параметром пара-замещенных фенола: n-метилфенол рК а 10,37. Полученные результаты хорошо согласуются с данными [6].

Таблица 1

Константы кислотной диссоциации пенициллинов (µ=0.1 КСl)

Равновесие	рК а	Равновесие	рК а
HBzp↔H++Bzp-	3.58±0.04	H3Amx+↔ H++H2Amx±	3.30±0.17
H2Amp+↔ H++HAmp±	3.26±0.12	H2Amx±↔ H++ HAmx-	7.66±0.08
HAmp±↔ H++Amp-	7.23±0.06	HAmx-↔ H++ HAmx2-	10.24±0.04

Комплексообразование меди (II) с бензилпенициллином, апициллином, амоксициллином

По методике [3] получали комплексное соединение меди(II) с антибиотиками и титровали раствором гидроксида натрия (рис. 5-7). При рН>4 во всех системах образуется новое соединение. При уменьшении кислотности среды ниже рН 4 протонируются карбоксильные группы лигандов (рК ~ 3) и комплексы разрушаются. По данным рН-метрии, были рассчитаны кривые образования комплексов (рис. 8-10). Для этого использовали ранее определенные значения констант кислотно-основных равновесий в растворах антибиотиков (табл. 1).

Характер кривых образования комплексов свидетельствует о том, что в системах возможно существование нескольких комплексных соединений. Это могут быть комплексы с различным соотношением Ме:L либо в состав комплекса металл и лиганд могут входить в разных формах: лиганд – в де-протонированной и протонированной, металл – в дегидролизованной и гидролизованной. С учетом констант диссоциации лигандов, более вероятной его формой является депротонированная. Существование же меди в виде Cu²⁺ и Сu(OH)⁺ вполне вероятно, учитывая константу гидролиза меди: lgК гидр = 6,7. На образование гидроксокомплексов указывают и авторы [2].

Взаимодействие меди с антибиотиками сопровождается изменением окраски растворов. Электронные спектры поглощения, записанные при различных значениях кислотности среды (рН 4-12) в интервале длин волн 300-500 нм, характеризуются наличием несимметричных полос, что указывает на присутствие в системе нескольких комплексных соединений. Характер полос поглощения позволяет предположить, что в данных системах зависимости от рН среды образуются два комплекса: в интервале рН 4-11 существует комплекс с максимальной оптической плотностью при длине волны 350 нм (рН опт 10-11), при рН>6 наблюдается появление второй, значительно менее интенсивной полосы поглощения, максимум которой батохромно сдвинут относительно первой (400 нм).

В аналитическом отношении более перспективны соединения, которым отвечают полосы поглощения с максимумом 350 нм. Различными методами показано (рис. 11-14), что во всех случаях соотношение Ме:L = 1:1 и, учитывая константу гидролиза меди, это гидроксокомплексы. Из кривых образования комплексов (рис. 8-10) видно, что точки перегиба нечеткие и условия, при которых находили константы диссоциации лигандов, реализуются не только при условиях, характерных для полуцелых значений n . Это сделало невозможным применение графического варианта метода Бьеррума, поэтому для определения констант устойчивости использовали расчетный способ.

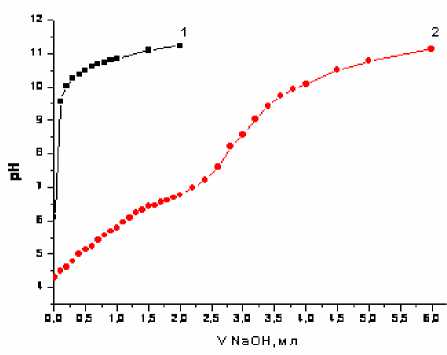
Рис. 5. Кривые рН-метрического титрования: 1 – Bzp-, 2 – Bzp-+Cu2+

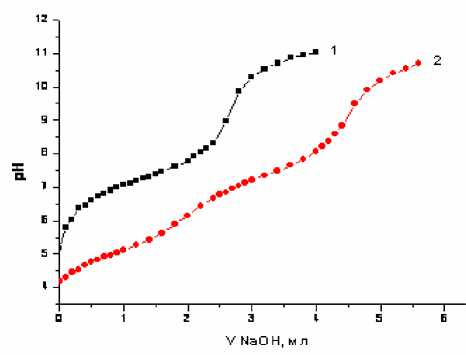
Рис. 6. Кривые рН-метрического титрования: 1 – HAmp, 2 – HAmp+Cu2+

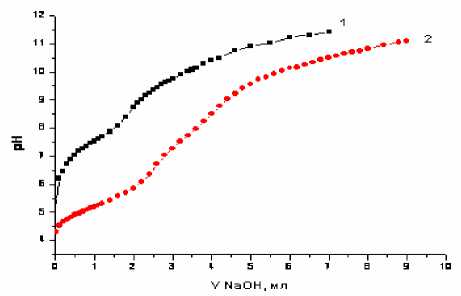
Рис. 7. Кривые рН-метрического титрования: 1 – HAmx, 2 – HAmx+Cu2+

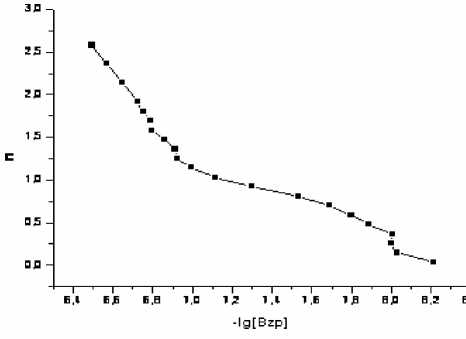
Рис. 8. Кривая образования комплексов Bzp с Cu2+     Рис. 9. Кривая образования комплексов Amp с Cu2+

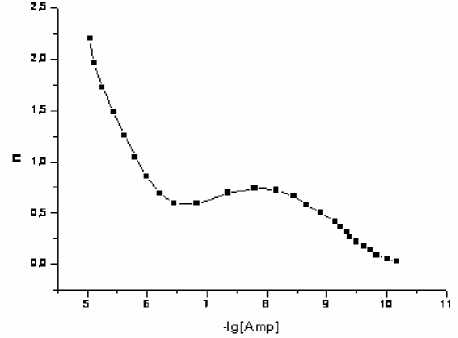
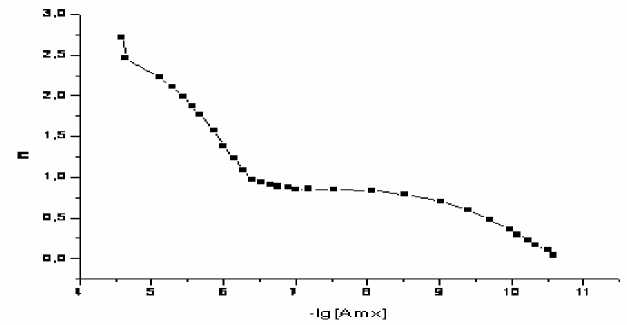
Рис. 10. Кривая образования комплексов Amх с Cu2+

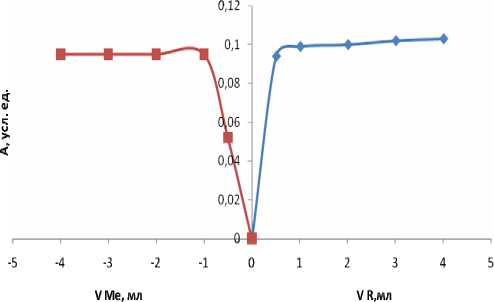
Рис. 11. Метод молярных отношений: С_Bzp= C_Cu = 2.8·10^-3 M (исх), рН 11, λ_max= 350 нм, l = 1 см, С_Bzp= const (слева), C_Cu= const (справа), V ф_{отометр} = 10 мл

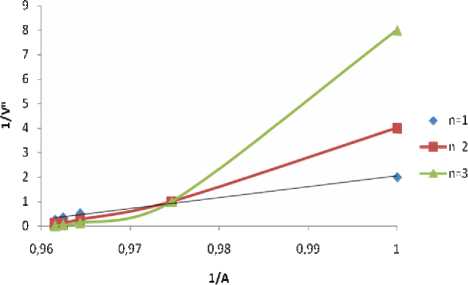
Рис. 12. Метод Асмуса: С_Amp= C_Cu= 2.7·10^-3 M (исх), рН 11, λ_max= 350 нм, l = 1 см, C_Cu= const, V ф_{о -} тометр = 10 мл, l = 1 см

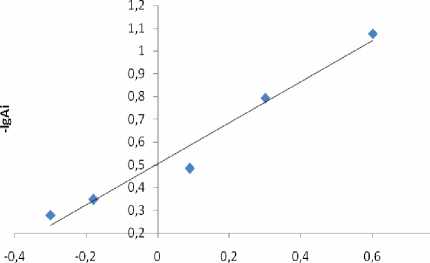
•IgCR

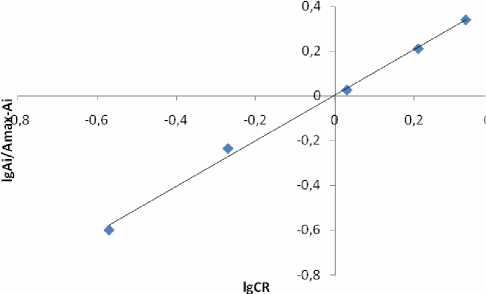
Рис. 13. Метод Бента-Френча. СAmx=CCu=2.5·10-3 M    Рис. 14. Метод сдвига равновесия. СAmp= CCu=2.7·10-3 M

(исх), рН 11, λ max = 350 нм, l = 1см, C Cu = const, V фото-    (исх), рН 11, λ max = 350 нм, l = 1см, C Cu = const, V фотометр = 10

_метр = 10 мл, l = 1 см                                             мл, l = 1 см

Ступенчатые константы устойчивости комплексов были рассчитаны по формуле:

_ n + 1 - n                     _ n = (n - П )[ L ] при условии, что n> n >n-1.

Находили средние значения К 1 в области 0,25< n <0,75, К 2 – в области 1.25< n <1,75. Результаты представлены в таблице 2.

Таблица 2

Ступенчатые и полные константы устойчивости комплексов пенициллинов с Cu2+

Лиганд	lgK 1	lgK 2	lgβ 1 =lgK 1	lgβ 2 =lgK 1 +lgK 2
Bzp	6.14±0.14	7.15±0.15	6.14±0.14	13.29±0.16
Amp	5.12±0.04	8.56±0.07	5.12±0.04	13.68±0.06
Amx	4.27±0.09	8.70±0.07	4.27±0.09	12.97±0.08

Количественное определение ампициллина

Наиболее чувствительной из рассмотренных реакций является реакция комплексообразования меди с ампициллином (ε CuBzp =340 моль^-1см^-1л, ε CuAmp =3890 моль^-1см^-1л, ε СuAmx =2620 моль^-1см^-1л). Именно эта реакция рассматривается в качестве аналитической для количественного определения ампициллина [3]. Однако, как уже было отмечено, в методике [3] отсутствуют нормативы контроля для оценки результатов определения.

Оценка метрологических параметров фотометрической методики количественного определения ампициллина и расчет нормативов контроля и осуществлялись различными способами: методом «введено-найдено», сравнением результатов с данными, полученными по аттестованной методике (ВЭЖХ) [7]. Было проведено определение ампициллина в препаратах различных производителей: ФГУП «Мосхимфармпрепараты» им. Н.А. Семашко, ЗАО «Верофарм», «Санавита» (Германия), ОАО «Биосинтез» (табл. 3).

Таблица 3

Результаты определения ампициллина

Проба	Биосинтез		Мосхимфармпрепараты		Верофарм		Санавита
	ВЭЖХ	ФТМ	ВЭЖХ	ФТМ	ВЭЖХ	ФТМ	ВЭЖХ	ФТМ
mAmp, г	0.2515	0.2501	0.2701	0.2656	0.2518	0.2456	0.2700	0.2649
	0.2585	0.2522	0.2632	0.2594	0.2531	0.2498	0.2587	0.2671
	0.2478	0.2501	0.2578	0.2698	0.2401	0.2415	0.2663	0.2606
	0.2489	0.2501	0.2545	0.2490	0.2453	0.2435	0.2609	0.2563
	0.2523	0.2543	0.2515	0.2573	0.2495	0.2456	0.2504	0.2563
m срAmp , г	0.2518	0.2514	0.2594	0.2602	0.2480	0.2452	0.2613	0.2610

Для обеих методов оценили воспроизводимость результатов измерений (табл. 4). Результаты хорошо соглас у ются между собой, значения с до в ерительными интервалами перекрываются:

ВЭЖХ: Х ± 5 = 0.2551 ± 0.0037 , ФТМ: Х ± 3 = 0.2545 ± 0.0038

Более строгая сравнительная оценка воспроизводимостей двух методов была проведена с использованием статистического метода проверки гипотез (метод нуль-гипотез) по критерию

⁵ ВЭЖХ

t • 5 2.09 • 0.0080

n

4.47

= 0.0037 З фотометр.

t • 5 2.09 • 0.0082

—р^ = ------------= 0.003 8

n

4.47

Фишера путем сравнения дисперсий (стандартных отклонений) двух выборок (ВЭЖХ и фотометрия):

V фотометр .     0,6652 • 10 - ⁴

F = . ----=------------ = 1,04

V ВЭЖХ      0,6414 • 10 - ⁴

Поскольку F эксп. табл , (F табл = 2.1), дисперсии однородны, т.е. воспроизводимость фотометрического метода и метода ВЭЖХ одинакова. Принимая во внимание однородность дисперсий, был рассмотрен вопрос о правильности фотометрического определения. Для этого применили способ сравнения средних значений выборок с однородной дисперсией:

5 = / ^{(0.0082 + 0.0080} ) = 0 0206 |Х 1 - Х 2 1=1 0.2545 - 0.2551 | = 0.0006

V 20 + 20 - 2        ■

П\ + n?                      20 + 20

t,S_A —----- = ± 1.96 • 0.0206 J --------= 0.0128

^p     n 1 n 2                           400

0.0006<0.0128 – систематическая погрешность отсутствует.

Оценка правильности с использованием коэффициентов Стьюдента также показала отсутствие систематической погрешности:

I0.2545 - 0.2551 I

J ¹ = 0.092 0.0206 J ²⁰ + ²⁰

t tтабл =1.96 (Р=0,95), экспер .

Поскольку методика определения ампициллина методом ВЭЖХ является нормативным документом, результат, полученный с использованием этой методики можно считать истинным. Это дало возможность оценить правильность фотометрической методики еще одним способом – сравнением среднего и истинного результата (табл. 5). За истинное значение µ принимали результат, полученный методом ВЭЖХ – 0.2551 г.

Экспериментально найденная разность между средним (фотометрия) и истинным (ВЭЖХ) результатами меньше доверительного интервала – при фотометрическом определении отсутствует систематическая погрешность.

Таблица 4

Оценка воспроизводимости результатов определения ампициллина фотометрическим методом и методом ВЭЖХ

n		X i	Х	(X i - Х )2 104	i ( X i - x ) 2 V = = --------10 4 n - 1	5 =1	n E ( Xi - X )2 i = 1	5, = 5 r X
							n - 1
	1	0.2501		0.1936
	2	0.2522		0.0529
	3	0.2501		0.1936
	4	0.2501		0.1936
	5	0.2543		0.0004
	6	0.2656		1.2321
	7	0.2594		0.2401
	8	0.2698		2.3409
	9	0.2490		0.3025
	10	0.2573	0.2545	0.0784	0.6652	0.0082		0.0320
	11	0.2456		0.7921
	12	0.2498		0.2209
	13	0.2415		1.6900
JS s у s a 2 о о e	14	0.2435		1.2100
	15	0.2456		0.7921
	16	0.2649		1.0816
	17	0.2671		1.5876
	18	0.2606		0.3721
	19	0.2563		0.0324
	20	0.2563		0.0324
	1	0.2515		0.1296
	2	0.2585		0.1156
	3	0.2478		0.5329
	4	0.2489		0.3844
	5	0.2523		0.0784
	6	0.2701		2.2500
	7	0.2632		0.6561
	8	0.2578		0.0729
	9	0.2545		0.0036
	10	0.2515	0.2551	0.1296	0.6414	0.0080		0.0313
	11	0.2518		0.1089
	12	0.2531		0.0400
	13	0.2401		2.2500
	14	0.2453		0.9604
	15	0.2495		0.3136
	16	0.2700		2.2201
	17	0.2587		0.1296
m m	18	0.2663		1.2544
	19	0.2609		0.3364
	20	0.2504		0.2209

Таблица 5

пп	X i	µ	(X i – µ)2 10-4	∑ n ( Xi - µ )2 V = i = 1            10 - 4 n - 1	∑ n ( X i - µ )2 S = i = 1 n - 1
1	0.2501		0.2500
2	0.2522		0.0841
3	0.2501		0.2500
4	0.2501		0.2500
5	0.2543		0.0064
6	0.2656		1.1025
7	0.2594		0.1849
8	0.2698		2.1609
9	0.2490		0.3721
10	0.2573	0.2551	0.0484	0.6696	0.0081
11	0.2456		0.9025
12	0.2498		0.2809
13	0.2415		1.8496
14	0.2435		1.3456
15	0.2456		0.9025
16	0.2649		0.9604
17	0.2671		1.4400
18	0.2606		0.3025
19	0.2563		0.0144
20	0.2563		0.0144

I x - µ I = 0. 2545 - 0.2551 = 0.0006                               δ = t^pS = 1.96 ^⋅ 0.0081 = 0.0036

n 4.47

Оценка правильности методом сравнения среднего и истинного значений

Расчет нормативов контроля для определения ампициллина фотометрическим методом

Для оценки нормативов контроля использовали метод «введено-найдено», для этого определение ампициллина проводилось в 5-ти параллелях проб без добавки и 5-ти параллелях с добавками ампициллина (табл. 6). Нормативы контроля рассчитывали по методике [8].

Значение характеристики суммарной погрешности оценивали по значениям характеристик ее составляющих (случайной и систематической): Δ = 1.96 × ^∆ 3 ^{2 c + σ ( ∆ о)2}

Отсутствие систематической погрешности (Δ с = 0) позволяет считать, что суммарная погрешность определяется наличием только случайной составляющей, т.е. значением стандартного отклонения (относительного стандартного отклонения), характеризующего воспроизводимость:

Δ = 1.96 × =1.96 × 5.51 = 10.80%.

Таблица 6

Оценка правильности определения ампициллина методом «введено-найдено» (P=0.95, n=5, f=4, t=2.78)

№	Проба без добавки а, мг	Введено а0, мг	Проба с добавкой, мг	Найдено а ij , мг	a ij – a 0	(a ij – a 0 )2·10-2	∑ k ∑ n ( a ij - a 0 )2 j = 1 i = 1 ·10-2	σ ∑	σ ~ ∑ r (отн. (ил σ и( ∆ )
1	5.90		9.15	3.25	0.25	6.25
2	5.95		9.00	3.05	0.05	0.25
3	5.90	3.00	8.75	2.85	-0.15	2.25	13.75	0.1658	5.51
4	5.90		8.70	2.80	-0.20	4.00
5	6.00		9.10	3.10	0.10	1.00
				aij =3.01	∑ ( aij - a0 ) = = 0 .05

Учитывая, что норматив контроля сходимости связан с показателем сходимости зависимостью d = 2,77 σ сх , а σ сх = ^{σ ( ∆ o )} / 1,5, рассчитали этот параметр: d = 2,77 × 5,51/1,5 = 10,18 % отн. ≈ 10% отн. от среднего результата анализа (0.10·х)

В.В. Тараскин, Л.Д. Раднаева, С.В. Жигжитжапова, О.А. Аненхонов, Ж. Ганбаатар. Сравнительный анализ состава эфирного масла PHLOJODICARPUS TURCZANINOVII SIPL. ( APIACEAE ), произрастающего в Монголии и Бурятии

Полученное значение норматива контроля сходимости позволило определить норматив контроля воспроизводимости: D = Q p,n x ^{а ( А} ) = 1,5 d = 2,77 x 5,51 = 15,27 = 15% отн. от среднего результата анализа (0.15·х).

Норматив контроля точности рассчитывали через суммарную характеристику погрешности анализа - показатель точности ( А ):

К = Δ = 10.80 % отн. для внешнего контроля.

К = 0.84 x 10.80 = 9.07 % отн. для внутрилабораторного контроля.

~ = 2 ( a ij - _a 0 )/ и = 0.05 /5 = 0.01 ~ = d ■ 100/a .. = 0.01 ■ 100 /3.01 = 0.33 %

O' 2 =

kn      ²

∑∑(aij - a0) j=1 i=1______________________ k • n

13.75 - 10^-2

= 0.1658

<~ 2 r = (<~ 2 /^a ij ) • Ю0% = (0.1658 • 100 %)/3.01 = 5.51%

= Я • V n ~\ = 0.33 ■ 2.24/5.51 = 0.13 t расч d r 2 ^r